2.6. Структура общего решения линейного неоднородного дифференциального уравнения (лнду) 2-го порядка

Теорема 1. Общее решение ЛНДУ 2-го порядка

(6.1)

представляется в виде суммы общего решения соответствующего однородного уравнения

(6.2)

и любого частного решения уравнения (6.1).

Доказательство. Докажем сначала, что будет решением уравнения (6.1). Для этого подставимв уравнение (6.1):. Это равенство является тождеством, так каки. Следовательно,есть решение уравнения (6.1).

Докажем теперь, что это решение является общим, то есть можно так выбрать входящие в него произвольные постоянные, что будут удовлетворяться любые начальные условия вида:

, . (6.3)

Согласно теореме о структуре общего решения линейного однородного дифференциального уравнения общее решение уравнения (6.2) можно представить в виде

,

где и– линейно независимые решения этого уравнения.

Таким образом: и, следовательно, начальные условия (6.3) можно записать в виде:

или

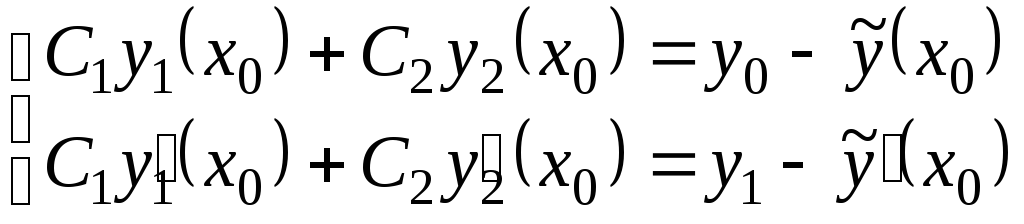(6.4)

Произвольные постоянные иопределяются из этой системы линейных алгебраических уравнений однозначно при любых правых частях, так как определитель этой системыесть значение определителя Вронского для линейно независимых решений уравнения (6.2) при, а такой определитель, как было указано выше, отличен от нуля. Определив постоянныеииз системы уравнений (6.4) и подставив их в выражение, мы получим частное решение уравнения (6.1), удовлетворяющее заданным начальным условиям. Теорема доказана.

Теорема 2. Если – решение дифференциального уравнения

,

а – решение уравнения

,

то функция является решением уравнения

. (6.5)

Доказательство. Подставив функцию в уравнение (6.5), получим .

Это равенство является тождеством, так как

и .

Теорема доказана.

2.7. Решение лнду 2-го порядка с постоянными коэффициентами со специальной правой частью

Рассмотрим случай, когда коэффициенты в уравнении (6.1) постоянны, то есть уравнение имеет вид:

(7.1)

где .

Рассмотрим метод отыскания частного решения уравнения (7.1) в случае, когда правая частьимеетспециальный вид. Это метод называется методом неопределённых коэффициентов и состоит в подборе частного решения в зависимости от вида правой части . Рассмотрим правые части уравнения (7.1) следующего вида:

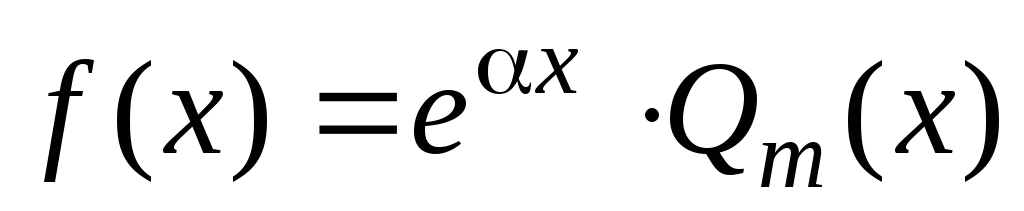1. , где 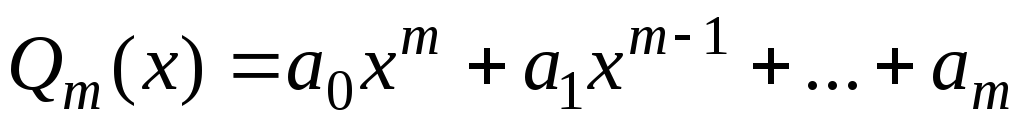– многочлен степени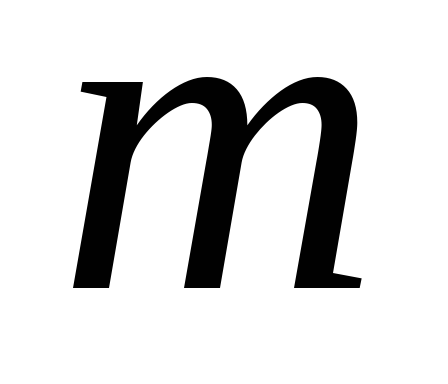, причём некоторые коэффициенты, кроме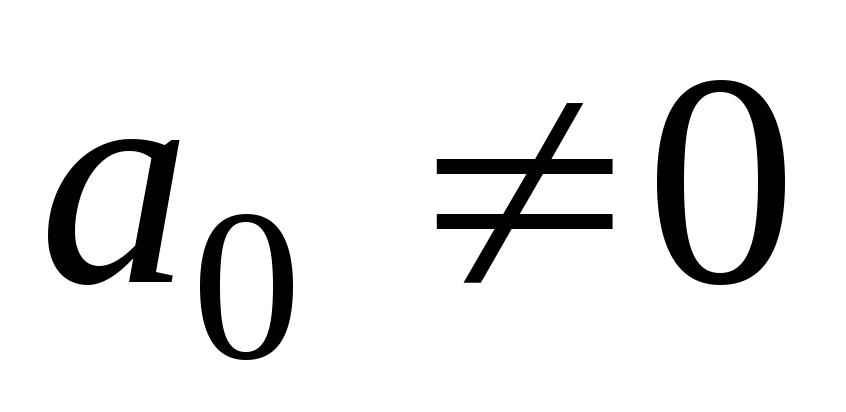, могут равняться нулю. Укажем вид частного решения в этом случае.

1. Если число не является корнем характеристического уравнения (5.2), то частное решение записываем в виде:

,

где – неопределённые коэффициенты, которые подлежат определению методом неопределённых коэффициентов.

Пример 1. Найти общее решение уравнения .

Решение. Для уравнения составляем характеристическое уравнение:. Откуда получаем. Следовательно, общее решение однородного уравнения есть

.

Правая часть заданного уравнения имеет специальный вид (случай 1), причёмне является корнем характеристического уравнения, поэтому частное решение ищем в виде:

,

где A, B – неопределённые коэффициенты.

Найдём производные первого и второго порядков и подставим их в заданное уравнение:

.

Сократим обе части на и приравняем коэффициенты при одинаковых степеняхx в левой и правой частях равенства:

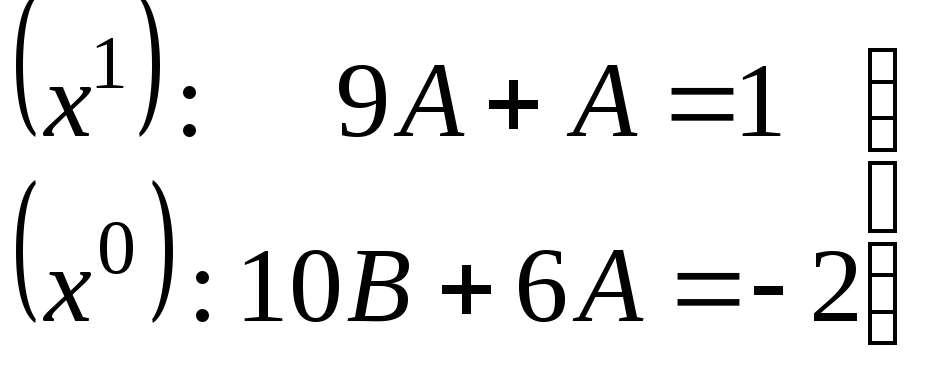
Из полученной системы уравнений находим: . Тогда, а общее решение заданного уравнения есть:

.

Если является корнем кратности соответствующего характеристического уравнения, то частное решение ищем в виде:

,

где – неопределённые коэффициенты.

Пример 2. Решить уравнение .

Решение. Соответствующее характеристическое уравнение имеет вид: , откуда. Тогда общее решение однородного уравненияесть:

.

Правая часть заданного уравнения имеет специальный вид (случай 1). Так как является корнем характеристического уравнения кратности, то частное решение ищется в виде:. Находим неопределённые коэффициентыA, B, C методом, изложенным в примере 1. В результате получаем . Окончательно имеем следующее выражение для общего решения:

.

2. Правая часть , где хотя бы одно из чиселM и N отлично от нуля. Укажем вид частного решения в этом случае.

1. Если число не является корнем характеристического уравнения (5.2), то частное решение ищем в виде:

,

где A, B – неопределённые коэффициенты.

2. Если число является корнем характеристического уравнения (5.2), причём кратность этого корня, то запишем частное решение в виде:

,

где A, B – неопределённые коэффициенты.

Пример 3. Решить уравнение .

Решение. Корнями характеристического уравнения для являются комплексно-сопряженные числа. В этом случае общее решение этого уравнения:.

Правая часть заданного в примере 3 уравнения имеет специальный вид: , где, а. Числоявляется корнем характеристического уравнения кратности, поэтому частное решение исходного уравнения примет вид:

.

Для определения A и B находим ,и подставляем в заданное уравнение:

.

Приводя подобные члены, приравнивая коэффициенты при и, получаем следующую систему:

,

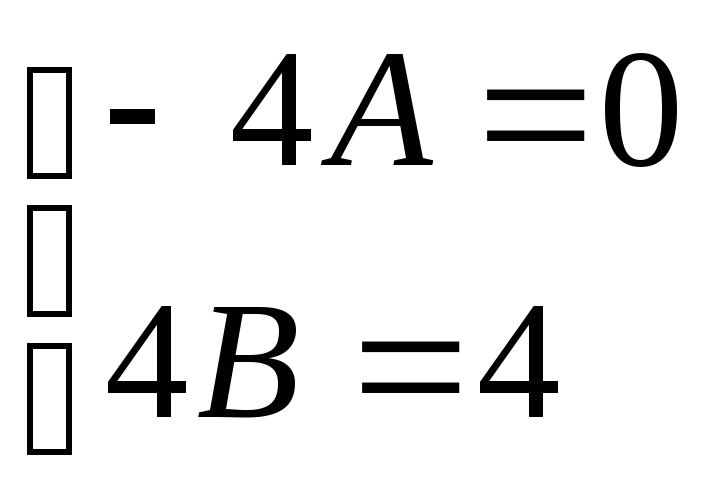отсюда .

Окончательно общее решение заданного уравнения имеет вид:

.

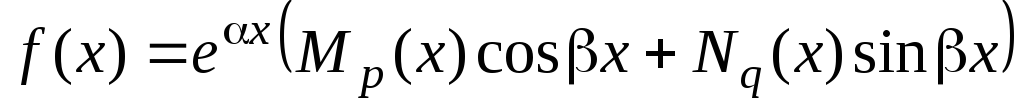3. , где и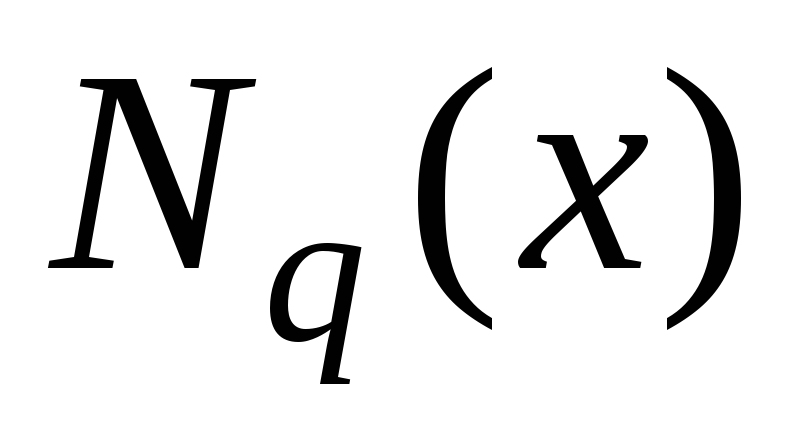– многочлены степени p и q соответственно, причём один из этих многочленов может равняться нулю. Укажем вид частного решения в этом общем случае.

1. Если число 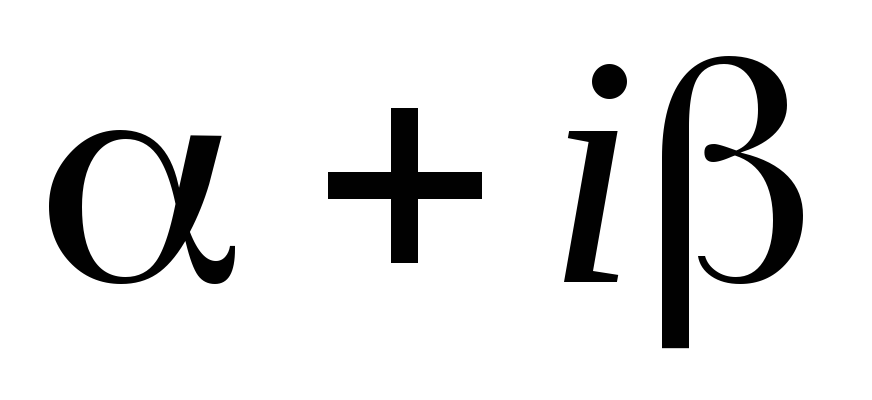не является корнем характеристического уравнения (5.2), то вид частного решения будет следующим:

(7.2)

где – неопределённые коэффициенты, а.

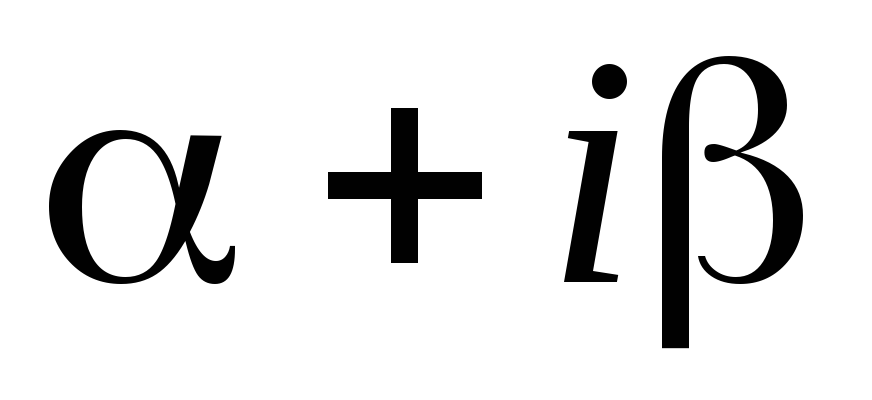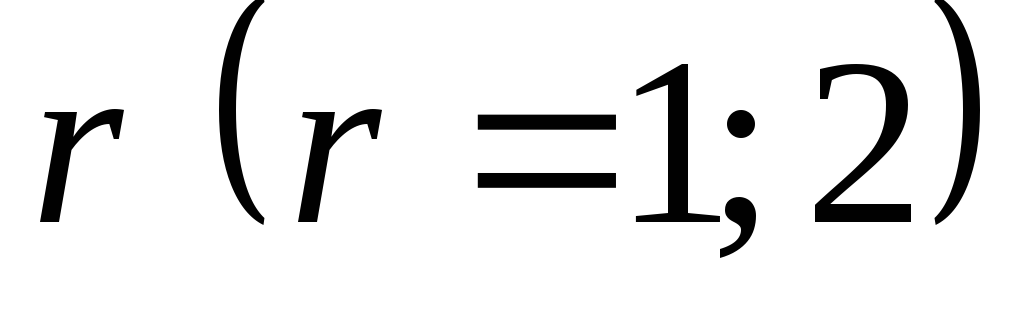2. Если число является корнем характеристического уравнения (5.2) кратности, то частное решение ЛНДУ примет вид:

, (7.3)

то есть частное решение вида (7.2) надо умножить на . В выражении (7.3)- многочлены с неопределёнными коэффициентами, причём их степень.

Пример 4. Указать вид частного решения для уравнения

.

Решение. Характеристическое уравнение имеет вид: . Его корни:. Общее решение ЛОДУ имеет вид:

.

Правая часть заданного уравнения имеет специальный вид (случай 3): . Числоявляется корнем характеристического уравнения кратности. Коэффициент приявляется многочленом первой степени, а при– нулевой степени, поэтому степень многочленов с неопределёнными коэффициентами надо брать.

Итак, вид частного решения:

.

Коэффициенты A, B, C, D могут быть определены по методу неопределённых коэффициентов.

Замечание. Если правая часть уравнения (7.1) есть сумма двух функций , где каждая из функций,имеет специальный вид (случаи 1-3), то частное решениеподбирается в виде суммы:, гдеесть частное решение для уравнения с правой частью, аесть частное решение для уравнения с правой частью.

Аналогично находятся частные решения в случае, когда правая часть уравнения есть алгебраическая сумма конечного числа функций специального вида, рассмотренного в случаях 1-3.