2.2. Линейное дифференциальное уравнение 2-го порядка

Определение. Линейное дифференциальное уравнение (ЛДУ) 2-го порядка имеет следующий вид:

, (2.1)

где и– заданные функции, непрерывные на том промежутке, на котором ищется решение.

Предполагая, что разделим (2.1) наи, после введения новых обозначений для коэффициентов, запишем уравнение в виде:

(2.2)

Примем без доказательства, что уравнение (2.2) имеет на некотором промежутке единственное решение, удовлетворяющее любым начальным условиям если на рассматриваемом промежутке функции,инепрерывны.

Если , то уравнение (2.2) называетсяоднородным, а именно линейным однородным дифференциальным уравнением (ЛОДУ), и уравнение (2.2) называется неоднородным в противном случае (то есть при ≢0 уравнение называется линейным неоднородным дифференциальным уравнением или ЛНДУ).

Рассмотрим свойства решений ЛОДУ 2-го порядка.

Определение. Линейной комбинацией функций называется выражение, где– произвольные числа.

Теорема. Если и– решения ЛОДУ

, (2.3)

то их линейная комбинация , где– произвольные числа, также будет решением этого уравнения.

Доказательство. Поставим выражение в уравнение (2.3) и покажем, что в результате получается тождество:

Перегруппируем слагаемые:

Поскольку функции иявляются решениями уравнения (2.3), то выражения в каждой из скобок в последнем уравнении тождественно равны нулю, что и требовалось доказать.

Следствие 1. Из доказанной теоремы вытекает при , что если– решение уравнения (2.3), тотоже есть решение этого уравнения.

Следствие 2. Полагая в теореме , получим, что сумма двух решений ЛОДУтакже является решением этого уравнения.

Замечание. Доказанное в теореме свойство решений остается справедливым для ЛОДУ любого порядка.

2.3. Определитель Вронского

Определение. Система функций называется линейно независимой на некотором промежутке, если ни одна из этих функций не представляется в виде линейной комбинации всех остальных.

В случае двух функций это означает, что , то есть. Последнее условие можно переписать в виде≢0 или 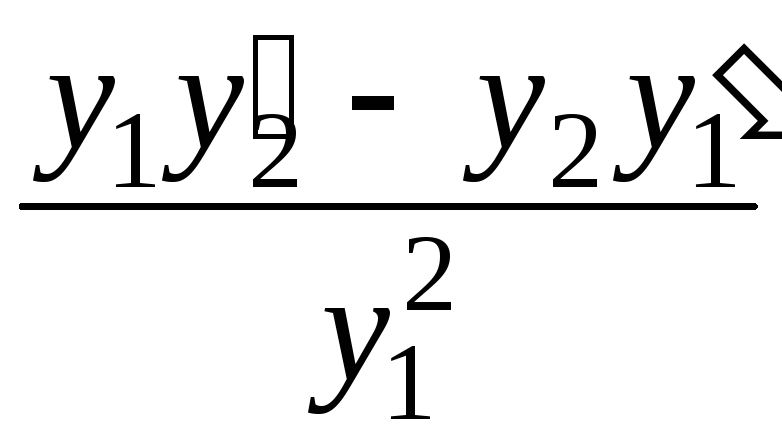≢0. Стоящий в числителе этого выражения определитель называетсяопределителем Вронского для функций и. Таким образом, определитель Вронского для двух линейно независимых функций не может быть тождественно равен нулю.

Пусть – определитель Вронского для линейно независимых решенийиуравнения (2.3). Убедимся подстановкой, что функцияудовлетворяет уравнению

. (3.1)

Действительно,

Поскольку функции иудовлетворяют уравнению (2.3), то

то есть – решение уравнения (3.1). Найдем это решение:

;

Отсюда

,

, ,

,.

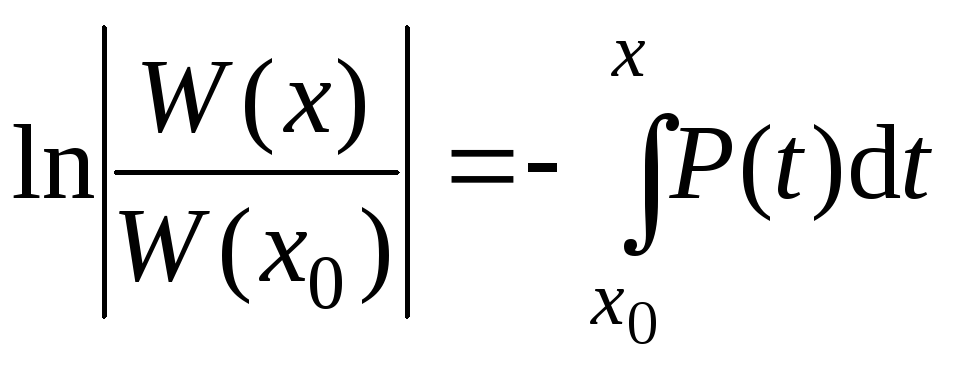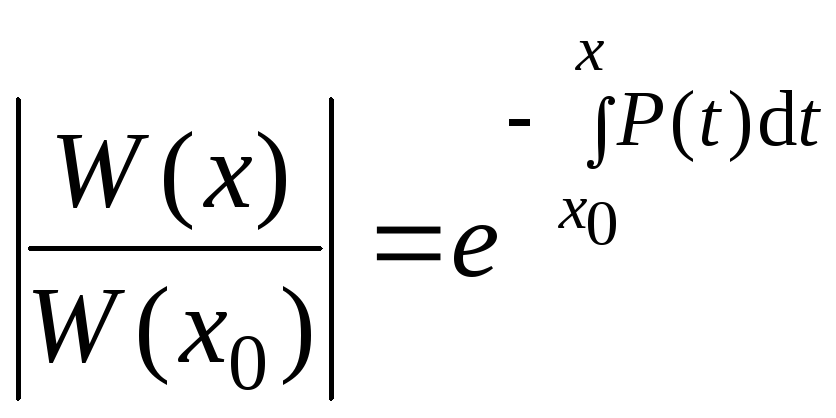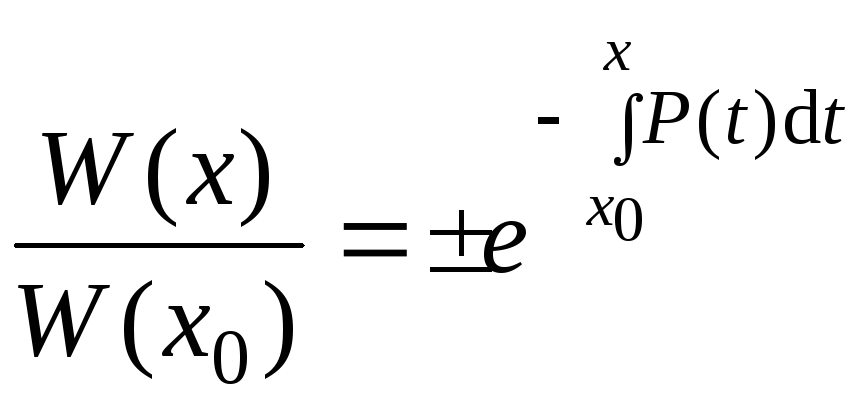В правой части последнего равенства необходимо оставить знак плюс, так как только в этом случае при получается тождество. Таким образом,

(3.2)

Полученная формула называется формулой Лиувилля.

Выше было показано, что определитель Вронского для линейно независимых функций не может быть тождественно равен нулю. Следовательно, существует такая точка , в которой определитель для линейно независимых решений уравнения (2.3)отличен от нуля. Тогда из формулы Лиувилля следует, что функциябудет отлична от нуля при всех значенияхиз рассматриваемого промежутка, поскольку при любом значении оба множителя в правой части формулы (3.2) отличны от нуля.