2.4. Структура общего решения лоду 2-го порядка

Теорема. Если и– линейно независимые решения линейного однородного дифференциального уравнения (2.3), то их линейная комбинация, гдеи – произвольные постоянные, является общим решением этого уравнения.

В данном случае говорят, что функции иобразуют фундаментальную систему решений ЛОДУ (2.3).

Доказательство. Первая часть утверждения, касающаяся того, что есть решение уравнения (2.3), следует из теоремы о свойствах решений ЛОДУ 2-го порядка. Остаётся показать, что решениебудетобщим, то есть надо показать, что при любых начальных условиях ,можно выбрать произвольные постоянныеи так, чтобы удовлетворить этим условиям. Запишем начальные условия в виде:

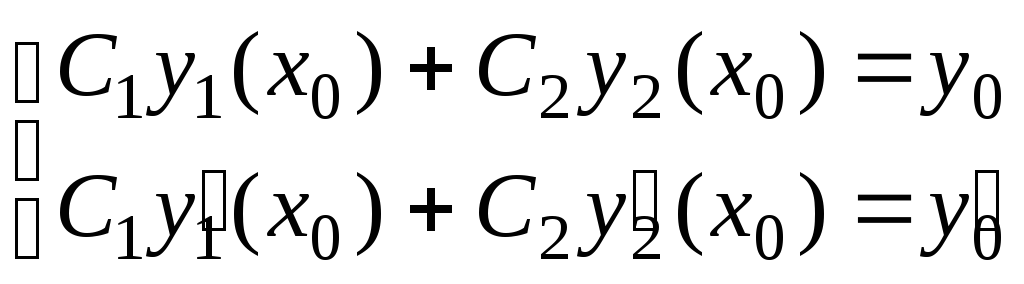
Постоянные и из этой системы линейных алгебраических уравнений определяются однозначно, так как определитель этой системы есть значение определителя Вронского для линейно независимых решений ЛОДУ при:

,

а такой определитель, как было показано в предыдущем параграфе, отличен от нуля. Теорема доказана.

Пример. Доказать, что функция , гдеи – произвольные постоянные, является общим решением ЛОДУ

Решение. Легко убедиться непосредственной подстановкой, что функции и удовлетворяют данному уравнению. Эти функции являются линейно независимыми, так как. Поэтому согласно теореме о структуре общего решения ЛОДУ 2-го порядка функция является общим решением данного уравнения.

2.5. Лоду 2-го порядка с постоянными коэффициентами

Рассмотрим ЛОДУ 2-го порядка с постоянными коэффициентами

(5.1),

где .

Согласно предыдущему параграфу общее решение ЛОДУ 2-го порядка легко определяется, если известны два линейно независимых частных решения этого уравнения. Простой метод нахождения частных решений уравнения с постоянными коэффициентами предложил Л. Эйлер. Это метод, который называется методом Эйлера, состоит в том, что частные решения ищутся в виде . Подставляя эту функцию в уравнение (5.1), после сокращения на, получим алгебраическое уравнение, которое называетсяхарактеристическим:

(5.2)

Функция будет решением уравнения (5.1) только при тех значениях , которые являются корнями характеристического уравнения (5.2). В зависимости от величины дискриминантавозможны три случая.

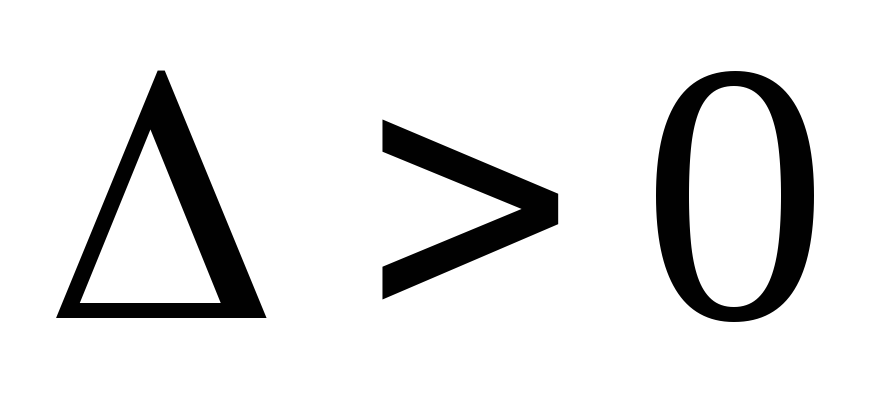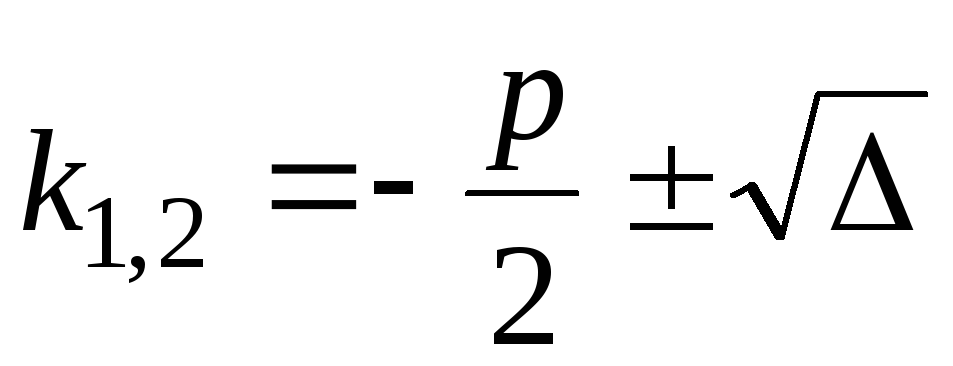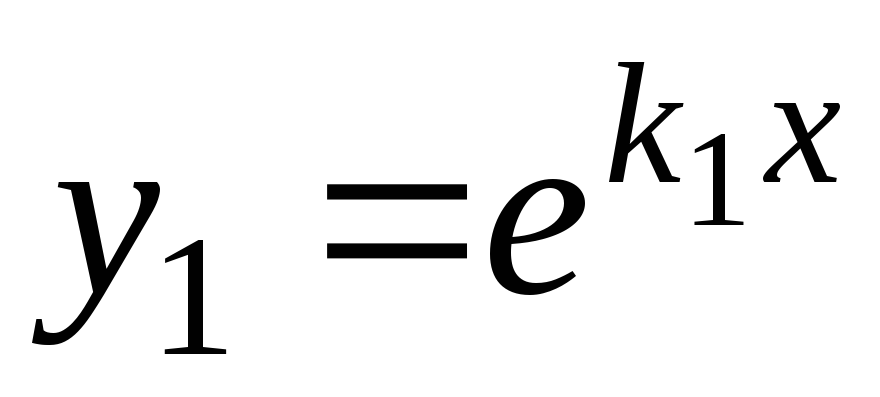1. . Тогда корни характеристического уравнения различны: . Решенияи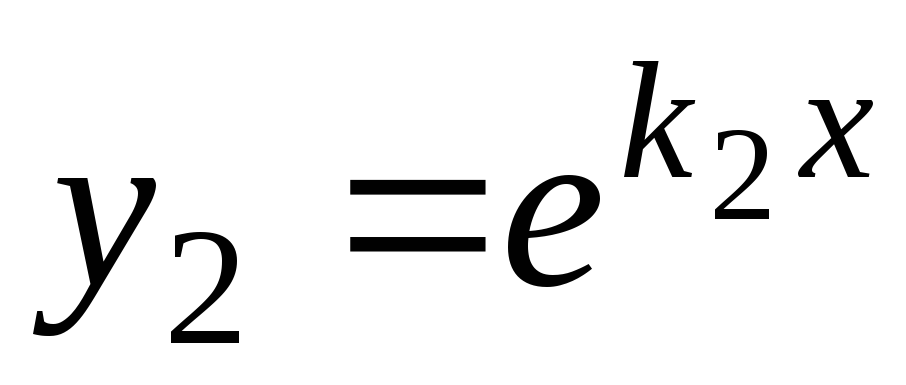будут линейно независимыми, так как и общее решение уравнения (5.1) можно записать в виде .

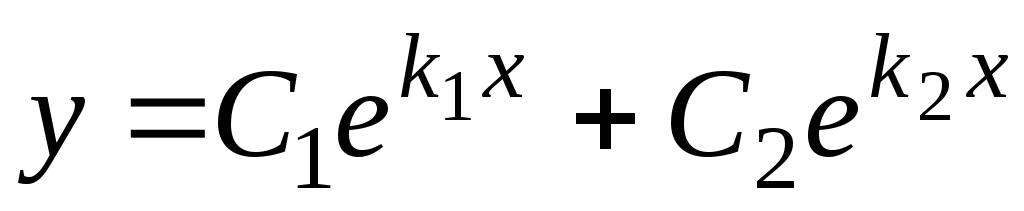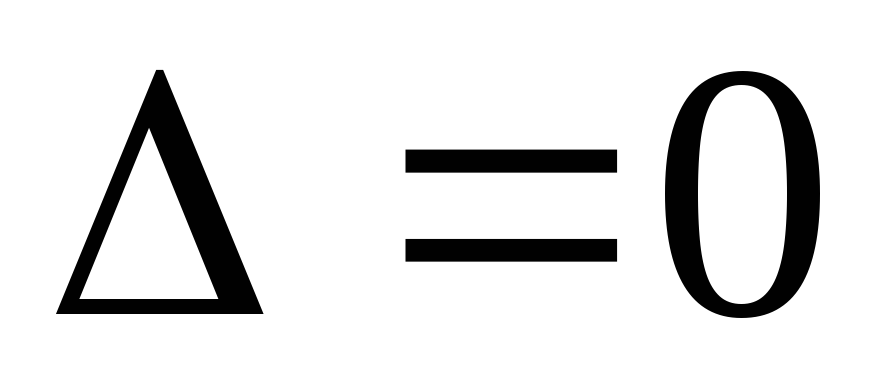2. . В этом случае 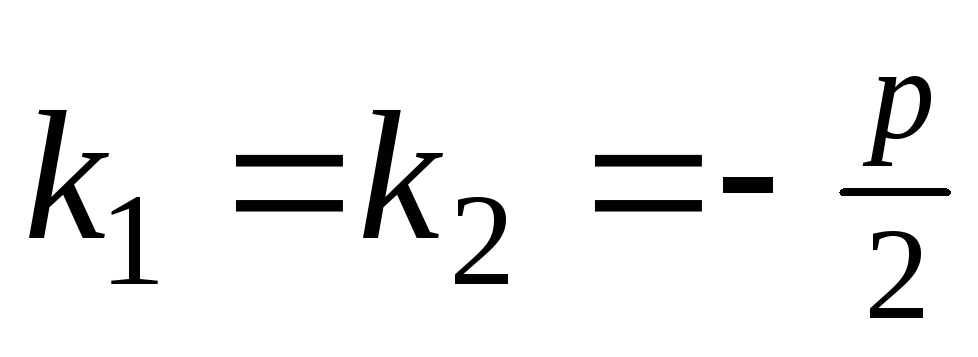и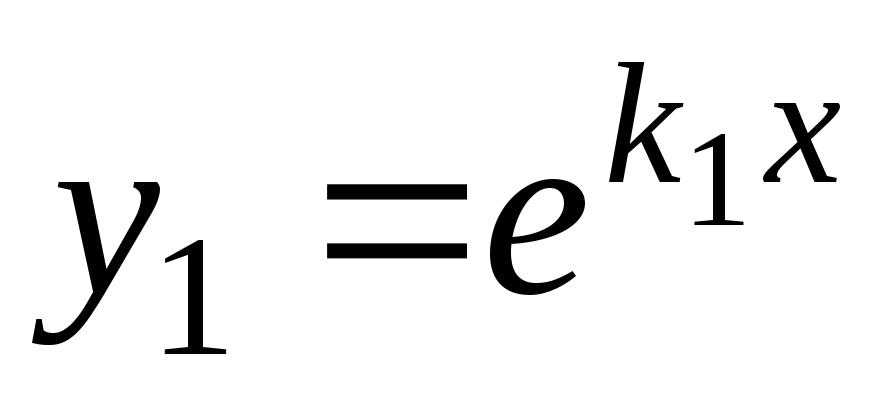. В качестве второго линейно независимого решения можно взять функцию. Проверим, что эта функция удовлетворяет уравнению (5.1).

Действительно,

,

.

Подставляя эти выражения в уравнение (5.1), получим

или

,

так как и.

Частные решения илинейно независимы, так как. Следовательно, общее решение уравнения (5.1) имеет вид:

или .

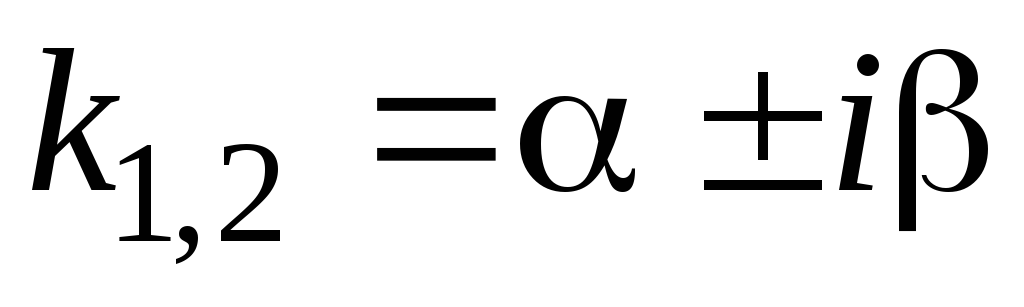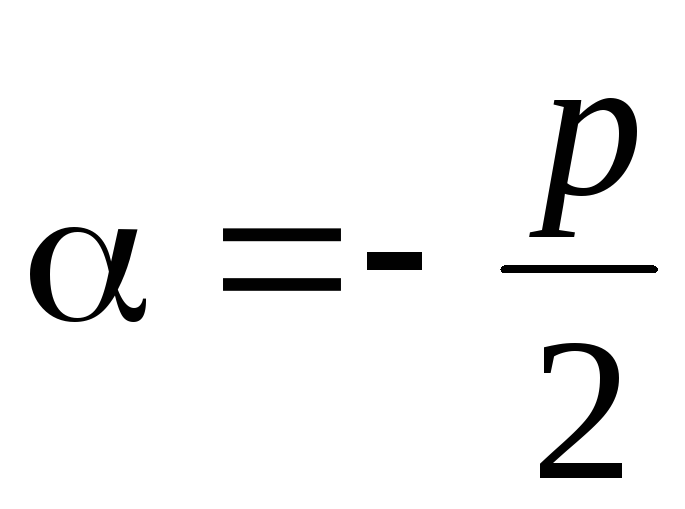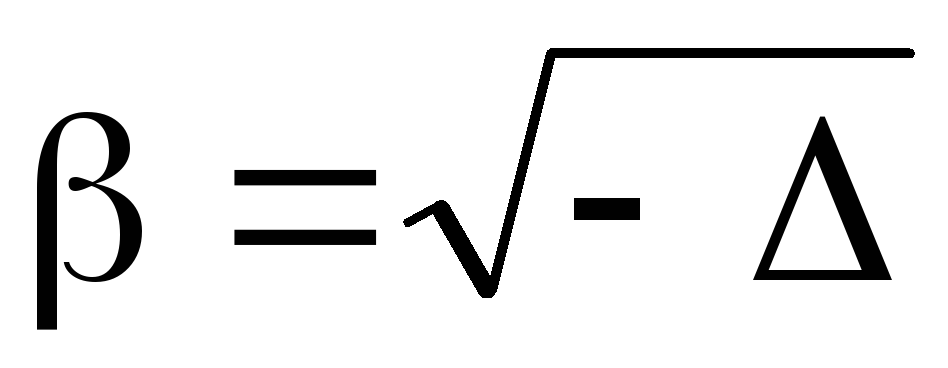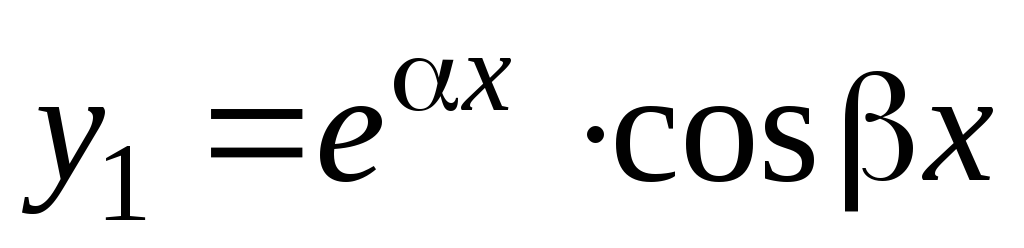3. . В данном случае корни характеристического уравнения комплексно-сопряжены: , где,. Легко проверить, что линейно независимыми решениями уравнения (5.1) будут функциии 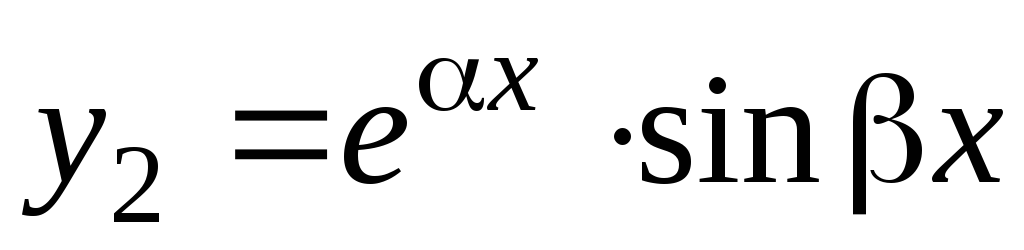. Убедимся, что уравнению (5.1) удовлетворяет, например, функция .

Действительно,

,

.

Подставив эти выражения в уравнение (5.1), получим

.

Выражения в обеих скобках в левой части этого равенства тождественно равны нулю. Действительно,

,

.

Таким образом, функция удовлетворяет уравнению (5.1). Аналогично нетрудно убедиться в том, что иесть решение уравнения (5.1). Поскольку, то общее решениебудет иметь вид:

.