1.8. Уравнение Бернулли

Определение. Дифференциальное уравнение вида

,

где ,, называетсяуравнением Бернулли.

Предполагая, что , разделим обе части уравнения Бернулли на.В результате получим:

. (8.1)

Введём новую функцию . Тогда

.

Домножим обе части уравнения (8.1) на и перейдем к функцииz(x):

,

то есть для функции z(x) получили линейное неоднородное уравнение 1-го порядка. Это уравнение решается методами, разобранными в предыдущем пункте 1.7. Подставим в его общее решение вместо z(x) выражение , получим общий интеграл уравнения Бернулли, который легко разрешается относительноy. При добавляется решение. Уравнение Бернулли можно также решать, не делая перехода к линейному уравнению путём подстановки, а применяя метод Бернулли, подробно разобранный в1.7. Рассмотрим применение этого метода для решения уравнения Бернулли на конкретном примере.

Пример. Найти общее решение уравнения:

. (8.2)

Решение. Уравнение (8.2) является уравнением Бернулли, причём .

Будем искать решение уравнения в виде . Тогда

.

В левой части последнего уравнения сгруппируем второе и третье слагаемые, которые содержат функцию u(x), и потребуем, чтобы . Откуда. Тогда для функцииu(x) получим следующее уравнение:

,

то есть

.

Последнее уравнение является уравнением с разделяющимися переменными для функции u(x). Решая его, приходим к:

,

,

.

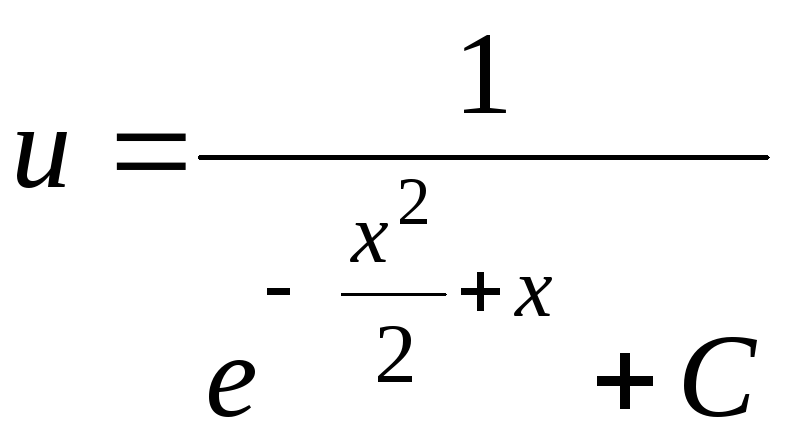Следовательно, общее решение данного уравнения (8.2) имеет вид:

.

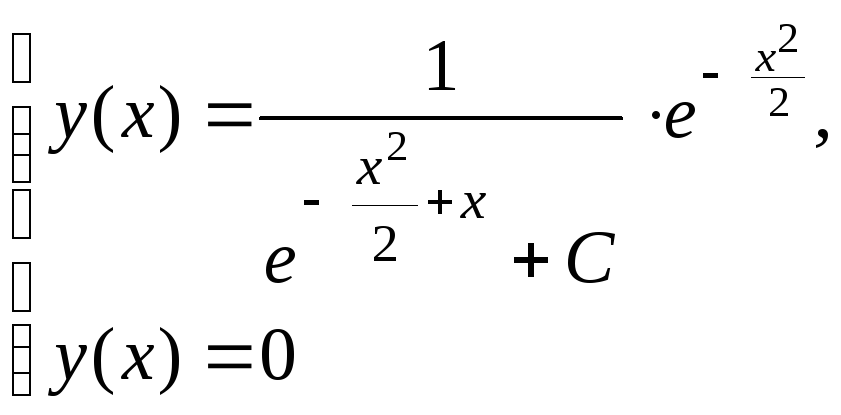1.9. Дифференциальные уравнения в полных дифференциалах

Определение. Если в уравнении

(9.1)

левая часть есть полный дифференциал некоторой функции , то оно называетсяуравнением в полных дифференциалах. Это уравнение можно переписать в виде , следовательно, его общий интеграл есть.

Например, уравнение есть уравнение в полных дифференциалах, так как его можно переписать в виде . А значит, общий интеграл задаётся равенством .

Теорема. Предположим, что функции M и N определены и непрерывны в некоторой односвязной области D и имеют в ней непрерывные частные производные соответственно по y и по x. Тогда, для того чтобы уравнение (9.1) было уравнением в полных дифференциалах, необходимо и достаточно, чтобы выполнялось тождество

. (9.2)

Доказательство. Доказательство необходимости этого условия очевидно. Поэтому докажем достаточность условия (9.2).

Покажем, что может быть найдена такая функция , чтои.

Действительно, поскольку , то

, (9.3)

где ‒ произвольная дифференцируемая функция.

Продифференцируем равенство (9.3) по y:

.

Но , следовательно,

.

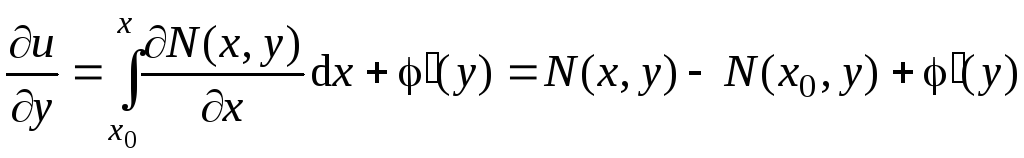Положим 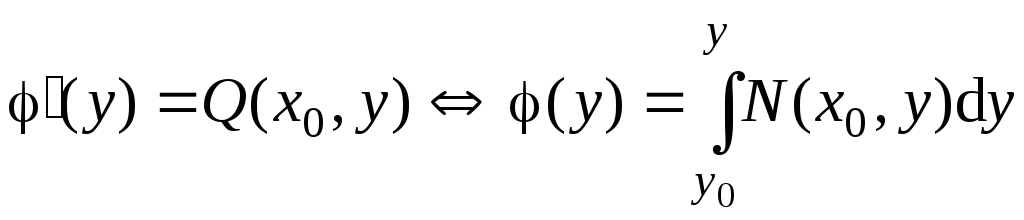и тогда.

Итак, построена функция 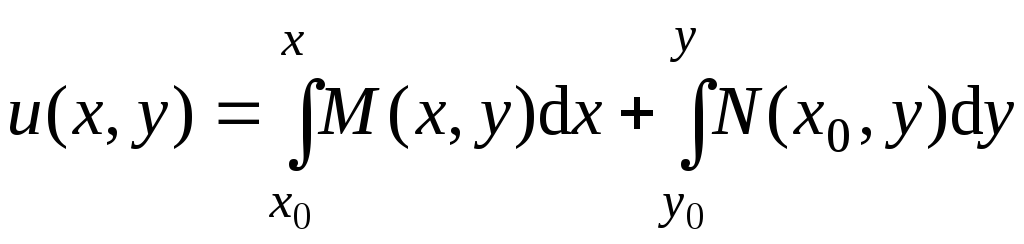, для которой, а.

Пример. Найти общий интеграл уравнения:

.

Решение. В данном случае Тогда

.

Следовательно, заданное дифференциальное уравнение 1-го порядка является уравнением в полных дифференциалах, то есть существует такая функция , частные производные которой соответственно поx и y равны и :

.

Проинтегрируем первое из двух соотношений по x:

,

.

Теперь продифференцируем поy и приравняем полученное в результате выражение частной производной :

.

Откуда и. Следовательно, общим интегралом заданного уравнения является:

.

1.10. Интегрирующий множитель

Определение. Если уравнение не является уравнением в полных дифференциалах и существует функция такая, что после домножения на неё обеих частей уравнения получающееся дифференциальное уравнение

становится уравнением в полных дифференциалах, то есть , то функцияназываетсяинтегрирующим множителем.

В случае, когда уравнение является уравнением в полных дифференциалах, полагают .

Если найден интегрирующий множитель µ, то интегрирование данного уравнения сводится к умножению обеих его частей на µ и нахождению общего интеграла полученного уравнения в полных дифференциалах.

Если µ есть непрерывно дифференцируемая функция от x и y, то

.

Из последнего тождества следует, что интегрирующий множитель µ удовлетворяет уравнению с частными производными 1-го порядка:

. (10.1)

Если заранее известно, что , где ω – заданная функция отx и y, то уравнение (10.1) сводится к обыкновенному (и притом линейному) уравнению с неизвестной функцией µ от независимой переменной ω:

, (10.2)

где

,

то есть указанная дробь является функцией только переменной ω.

Решая уравнение (10.2), находим интегрирующий множитель

, .

В частности, уравнение имеет интегрирующий множитель, зависящий только от x () или только отy (), если выполнены соответственно следующие условия:

, ,

или

, .
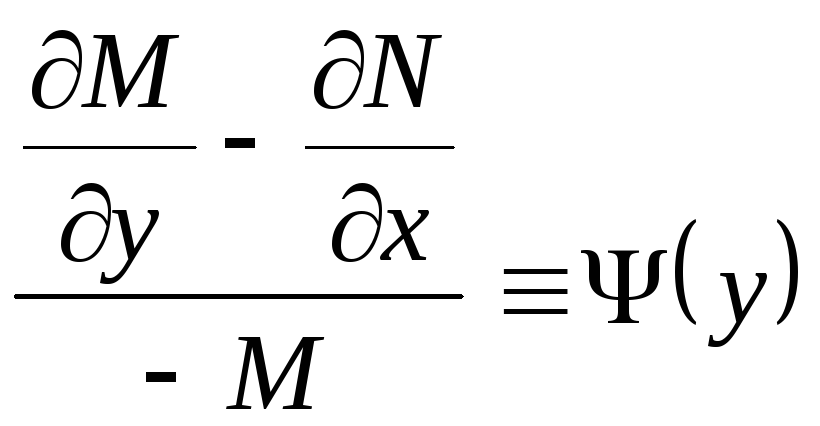