3.2. Линейное однородное дифференциальное уравнение с постоянными коэффициентами

Линейное однородное дифференциальное уравнение с постоянными коэффициентами имеет вид:

, (2.1)

где – постоянные вещественные числа. Это уравнение имеет фундаментальную систему решений , определенную при всехx и состоящую из степенных, показательных и тригонометрических функций. Соответствующее этой системе функций общее решение

определено в области ,,, …,, то есть во всем пространстве.

Построение фундаментальной системы решений ЛОДУ проводится методом Эйлера, который состоит в том, что частное решение ЛОДУ ищется в виде , где– некоторое число, подлежащее определению. Подставляя эту функцию в уравнение (2.1) и сокращая на, получим характеристическое уравнение:

. 2.2)

Его корни называются характеристическими числами уравнения (2.1). Рассмотрим возможные ситуации, возникающие при решении характеристического уравнения.

1. Все корни характеристического уравнения (2.2) различны и вещественны. Обозначим их 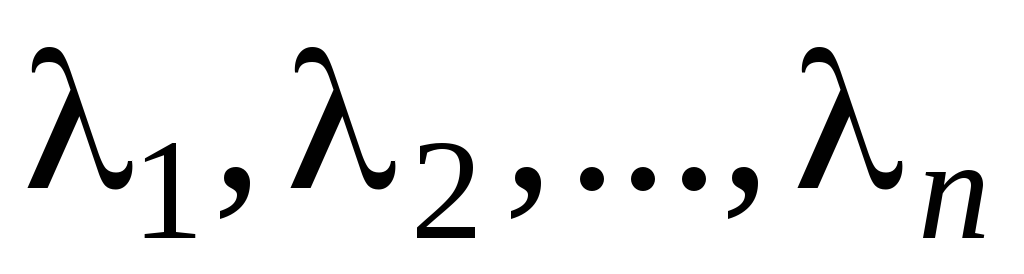. Тогда фундаментальную систему решений составляют функции: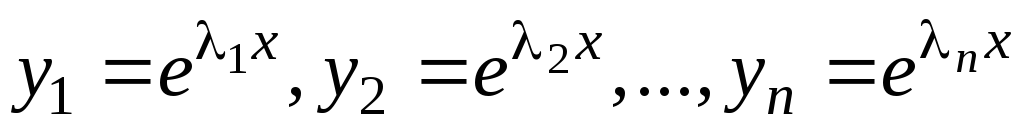, а общее решение имеет вид:

.

2. Все корни характеристического уравнения (2.2) различны, но среди них имеются комплексные. Пусть 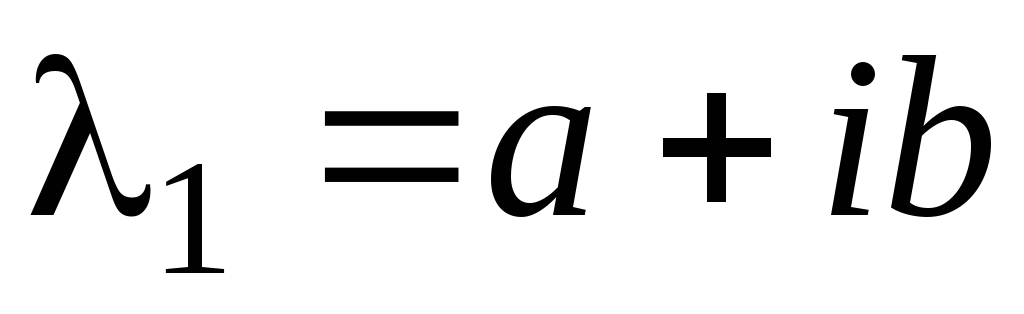– комплексный корень характеристического уравнения. Тогда тоже будет корнем этого уравнения. Этой паре корней соответствует пара линейно независимых частных решений:

.

Записав линейно независимые частные решения, соответствующие другим сопряжённым парам комплексных корней и всем вещественным корням, получим фундаментальную систему решений. Линейная комбинация этих решений с произвольными постоянными коэффициентами даст общее решение уравнения (2.1).

3. Среди корней характеристического уравнения имеются кратные. Пусть – вещественный k-кратный корень. Тогда ему соответствует k линейно независимых частных решений вида 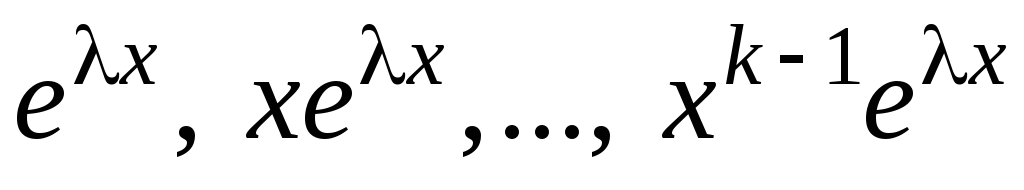, а в формуле общего решения – выражение вида.

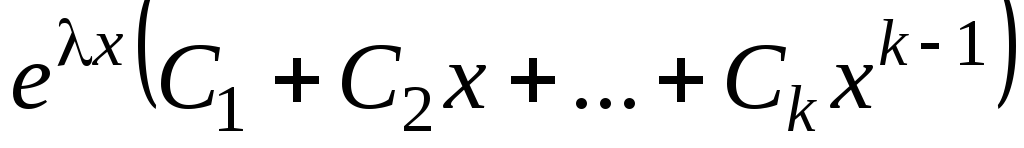4. Если – комплексный корень характеристического уравнения кратности k, то ему и сопряжённому с ним корню той же кратности соответствуют 2k линейно независимых частных решений вида:

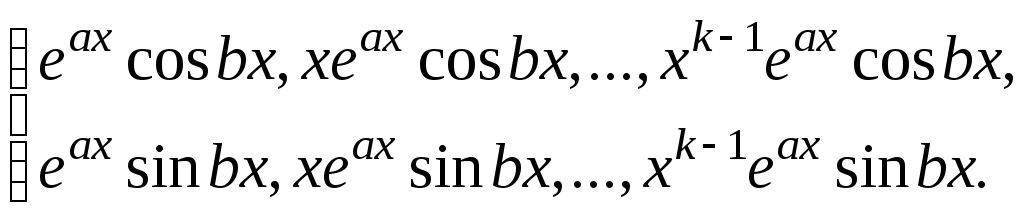
В формуле общего решения этим корням соответствует выражение вида:

.

Записав линейно независимые частные решения указанного выше вида, соответствующие всем простым и кратным вещественным корням, а также сопряжённым парам простых и кратных комплексных корней, получим фундаментальную систему решений. Линейная комбинация этих решений с произвольными постоянными коэффициентами даст общее решение уравнения (2.1).

4. Системы обыкновенных дифференциальных уравнений

4.1. Нормальные системы

Определение 1. Нормальная система обыкновенных дифференциальных уравнений имеет следующий вид:

(1.1)

где , – неизвестные функции от независимой переменнойx, подлежащие определению; ,– известные функции от, заданные и непрерывные в некоторой области. Числоn называется порядком системы (1.1). В дальнейшем ограничимся рассмотрением систем второго порядка ().

Определение 2. Пусть дана нормальная система уравнений

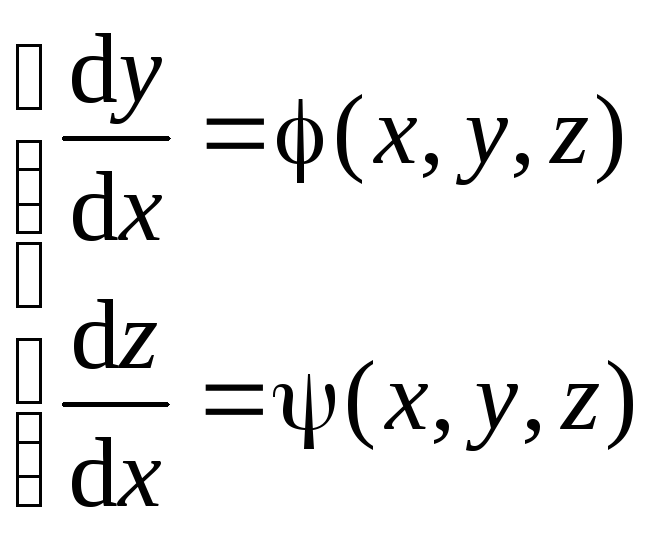(1.2)

где и– заданные непрерывные в некоторой области функции. Пара функций, определенных на интервале, имеющих непрерывные производные и удовлетворяющих наобоим уравнениям системы (1.2), называется еёрешением.

Задача нахождения решения , удовлетворяющего начальным условиям, где– заданные числа (начальные данные), называетсязадачей Коши.

Теорема существования и единственности решения задачи Коши. Пусть дана система уравнений (1.2) и пусть в некоторой области D(x, y, z) функции инепрерывны и имеют непрерывные частные производные поy, z. Пусть точка . Тогда существуют интервали определенные на нем непрерывно дифференцируемые функции, удовлетворяющие системе уравнений (1.2) и начальным условиям, причём эти функции определяются однозначно.