6. Комплексные выражения синусоидальной функции времени, ее производной и интеграла см. В табл. 1.

Таблица 1.

Временная и комплексная записи	Функция	Производная функции	Интеграл от функции
Запись во временной области	a =Am sin(t + )	Amcos(t + )	cos(t+ )
Комплексная функция времени	Amej(t +  )	Amej(t +  +  / 2)	Amej(t + -  /2)
Комплексная амплитуда	m = A m ej	jm	m
Комплексное действующее значение	= A m ej	j

Например, для тока i, падения напряжения на активном сопротивлении u_R, индуктивности u_L и емкости u_Cсоответствующие комплексные амплитуды запишем так :

i = I_m sin(t    _m = I_me^j ;

u_R = iR = RI_m sin (t    _Rm = R_m ;

u_L = LLI_m cos(t + )  _Lm = jL_m

u_C = 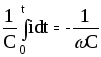I_m cos(t + )  _Cm = - j_m

Здесь стрелка означает знак соответствия.

7. Элементы электрической цепи переменного тока: пассивные и активные.

В табл. 2. приведены пассивные элементы, их изображения и обозначения, формы записи сопротивления и проводимости.

Таблица 2.

Наименование элемента	Свойства элемента	Изображение и буквенное обозначение	Сопротив-ление при синусоид. токе	Запись сопротивле-ния в комп- лексной форме	Проводи- мость при синусоид. токе	Запись про- водимости в комплекс- ной форме
Резистор	Эл. сопротив-ление	R	R	R	g = 1/R	g = 1/R
Индуктивная катушка	Индуктив- ность	L	xL=L	ZL= jL	bL=	YL=1/ZL= = - jbL
Конденсатор	Емкость	C	xC =1/C	ZC=- j	bC = C	YC=1/ZC= = jbC

8. Законы Ома и Кирхгофа для цепей переменного тока.

Закон Ома:

,

где Z - комплексное сопротивление участка цепи.

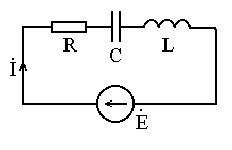
Например, для изображенной ниже цепи (рис. 15), Z = R+j(x_L-x_C) и закон Ома: (считаем источник э.д.с. идеальным ).

рис. 15

Первый закон Кирхгофадля мгновенных и комплексных токов соответственно :

_k = 0 ;_k = 0 .

Второй закон Кирхгофадля мгновенных и комплексных напряжений и э.д.с. соответственно :

_k =R_ki_k+u_Lk+u_Ck) ; 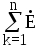_k =Z_k

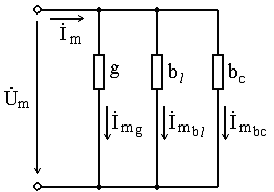
9. Последовательное и параллельное соединение сопротивлений и проводимостей.

На рисунках 16 и 17 изображены соответственно последовательная и параллельная электрические цепи :

При последовательном соединении: Z=_k

При параллельном соединении: Y=_k

рис. 16	рис. 17

Формулы для преобразования последовательной цепи в параллельную и для выполнения обратного преобразования имеют вид :

Y == = g - jb ; g = ; b = ;

Z = = R + jX ; R = ; X =

(здесь g и b - соответственно активная и реактивная проводимости; R и X - активное и реактивное сопротивления).

Замечание : необходимо помнить, что взаимообратными являются лишь комплексы Z и Y , а их составляющие R и g, x и b не являются таковыми.

10. О применимости методов расчета цепей постоянного тока к расчетам цепей синусоидального тока.

Структура формул законов Ома и Кирхгофа для цепей постоянного и синусоидального тока идентичны, поэтому методы расчета цепей постоянного тока, базирующиеся на законах Кирхгофа, могут быть использованы при расчете цепей переменного тока в случае применения комплексов.