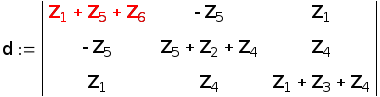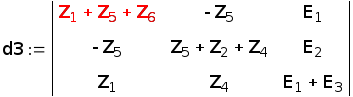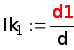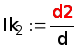6. Расчет методом трансфигурации
В соответствии с заданным вариантом из таблиц 1.1 и 1.2 выбираем схему и ее параметры.
|
Параметры элементов схемы. |
| |
|
r1= 0, Ом r2= 5, Ом r3=10, Ом r4=10, Ом r5=15, Ом r6=15, Ом |
E1=35, В E2=20, В E3=35, В | |
Преобразование из звезды в треугольник.
|
|
|
|
r36=40, Ом | |
|
| |
|
r64=40, Ом | |
|
| |
|
r43=26.667, Ом | |
|
| |
|
r564=10.909, Ом |
Полученную схему решаем методом контурных токов.
Решаем систему с помощью определителей.
|
|
d = 2.398∙104 |
|
|
d1 = 9.591∙104 |
|
|
d2 = -6.023∙10-13 |
|
|
d3 = -3.297∙104 |
Контурные токи.
|
|
Ik1= 4, A |
|
|
Ik2= 0, A |
|
|
Ik3=-1.375, A |
Реальные токи.
|
|
I5=-1, A |
|
|
I1= 4, A |
|
|
I3= 4, A |
|
|
I2= 0, A |
|
|
I6=-1, A |
|
|
I4= 3, A |
Проверка баланса.
Pn=280, Вт
Pi =280, Вт
Баланс сошелся.
Пример расчёта простых цепей переменного тока символическим методом
|
|
- задание интервала |
|
|
- введение в расчет комплексного числа |
|
|
- обозначение числа Пи |
|
|
- задание интервала изменения времени |
В соответствии с заданным вариантом из таблиц 1.1 и 1.2 выбираем схему и ее параметры.
|
Параметры элементов схемы. |
| |
|
r1 := 2 , Ом r2 := 0 , Ом r3 := 4 , Ом r4 := 3 , Ом r5 := 5 , Ом r6 := 6 , Ом |
x1 := 4 , Ом x2 := 7 , Ом x3 := 3 , Ом x4 := 0 , Ом x5 := 4 , Ом x6 := 4 , Ом | |
Параметры источников ЭДС :
E1=0, В
Е2=90 ePi/3 j, B
Е3=40, B
Определение комплексных сопротивлений:
|
|
|
|
|
|
|
|
|
Схема участка цепи:
|
Z1= 2 - 4j, Ом |
-R-C- |
|
Z2= 7j, Ом |
--L-- |
|
Z3= 4 - 3j, Ом |
-R-C- |
|
Z4= 3, Ом |
--R-- |
|
Z5= 5 - 4j, Ом |
-R-C- |
|
Z6= 6 + 4j, Ом |
-R-L- |
Рассчитаем комплексные токи на участках цепи методом контурных токов. Для чего составим уравнения по второму закону Кирхгофа для контурных токов и решим их при помощи определителей
Ik1•(Z1 + Z5 + Z6) - Ik2•Z5 + Ik3•Z1 =E1
-Ik1•Z5 + Ik2•(Z5 + Z2 + Z4) + Ik3•Z4 =E2
Ik1•Z1 + Ik2•Z4 + Ik2•(Z1 + Z3 + Z4) = Е1 + Е3
|
|
d = 1.259∙103 + 42j |
|
|
d1 = 5.784∙103 + 422.327j |
|
|
d2 = 1.188∙104 + 4.477∙103j |
|
|
d3 = – 322.691 + 1.108∙103j |
Hаходим контурные токи:
|
|
Ik1= 4.578 - 0.488j, A |
|
|
Ik2= 9.541 + 3.238j, A |
|
|
Ik3=-0.227 + 0.888j, A |
Находим реальные токи путем наложения соответствующих контурных токов:
|
I1=Ik1 + Ik3 |
I1= 4.351 + 0.399j, A |
|
I2=Ik2 |
I2= 9.541 + 3.238j, A |
|
I3=Ik3 |
I3=-0.227 + 0.888j, A |
|
I4=Ik2 + Ik3 |
I4= 9.315 + 4.125j, A |
|
I5=Ik2 - Ik1 |
I5= 4.963 + 3.726j, A |
|
I6=Ik1 |
I6= 4.578 - 0.488j, A |
По закону Ома находим падения напряжений на всех участках цепи:
|
U1=I1∙Z1 |
U1= 10.300 - 16.606j, B |
|
U2=I2∙Z2 |
U2=-22.665 + 66.790j, B |
|
U3=I3∙Z3 |
U3= 1.756 + 4.230j, B |
|
U4=I4∙Z4 |
U4= 27.944+12.376j, B |
|
U5=I5∙Z5 |
U5= 39.721 - 1.223j, B |
|
U6=I6∙Z6 |
U6= 29.421 + 15.383j, B |
Находим сопряженные комплексы токов:
|
Js1=Re(I1) - Im(I1)∙j |
Js1= 4.351 - 0.399j, A |
|
Js2=Re(I2) - Im(I2)∙j |
Js2= 9.541 - 3.238j, A |
|
Js3=Re(I3) - Im(I3)∙j |
Js3=-0.227 - 0.888j, A |
|
Js4=Re(I4) - Im(I4)∙j |
Js4= 9.315 - 4.125j, A |
|
Js5=Re(I5) - Im(I5)∙j |
Js5= 4.963 - 3.726j, A |
|
Js6=Re(I6) - Im(I6)∙j |
Js6= 4.578 +0.488j, A |
Находим комплексы мощности нагрузки:
|
Sn1=U1∙Is1 |
Sn1= 38.187 - 76.373j, BA |
|
Sn2=U2∙Is2 |
Sn2= 710.649j, BA |
|
Sn3=U3∙Is3 |
Sn3= 3.357 - 2.517j, BA |
|
Sn4=U4∙Is4 |
Sn4= 311.346, BA |
|
Sn5=U5∙Is5 |
Sn5= 192.59 - 164.072j, BA |
|
Sn6=U6∙Is6 |
Sn6= 127.179 + 84.786j, BA |
Находим комплексы мощности источников:
|
Si1=E1∙Is1 |
Si1= 0, BA |
|
Si2=E2∙Is2 |
Si2= 681.726 + 597.974j, BA |
|
Si3=E3∙Is3 |
Si3=-9.068 - 35.502j, BA |
Проверка баланса мощностей:
Sn=672.658 + 562.472j, BA
Si=672.658 + 562.472j, BA
Баланс сошелся.
Уравнения мгновенных значений напряжений:
Уравнения мгновенных значений токов:
