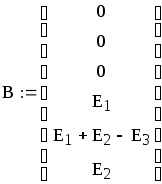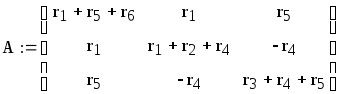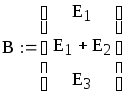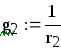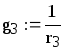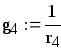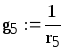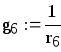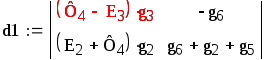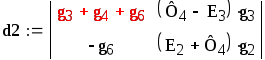8. Примеры расчета сложных цепей постоянного тока

   1. Расчет по законам Кирхгофа

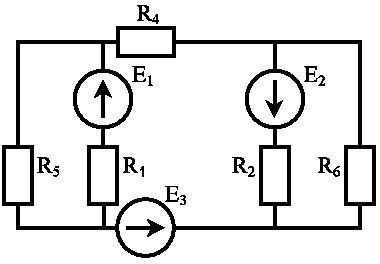
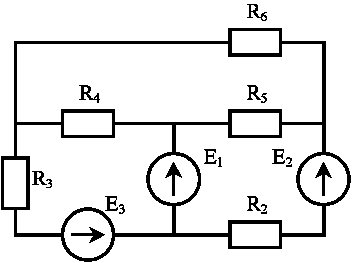
В соответствии с заданным вариантом из таблиц 1.1 и 1.2 выбираем схему и ее параметры.

Параметры элементов схемы.
r1 = 5, Ом r2 = 20, Ом r3 = 0, Ом r4 = 10, Ом r5 = 5, Ом r6 = 15, Ом	E1= 40, В E2= 15, В E3= 5, В

Уравнения по первому закону Кирхгофа.

Уравнения по второму закону Кирхгофа.

Решаем систему линейных уравнений матричным методом относитель- но неизвестных токов.

Для чего составляем две матрицы. Матрицу A, состоящую из коэфи- циентов, стоящих в правой части системы. И матрицу B, состоящую из коэфициентов, стоящих в левой части системы. После умножения транс- портированной матрицы A на B получим матрицу C.

I₁=C₀ I₁= 4.508, A

I₂=C₁ I₂= 0.864, A

I₃=C₂ I₃=-1.017, A

I₄=C₃ I₄= 1.017, A

I₅=C₄ I₅= 3.492, A

I₆=C₅ I₆=-0.153, A

Все источники э.д.с. работают как источники энергии, так как действительные направления токов в них совпадают с направлениями э.д.с.

Проверка баланса:

Pn=188.22, Вт

Pi =188.22, Вт

Баланс сошелся.

2. Расчет методом контурных токов

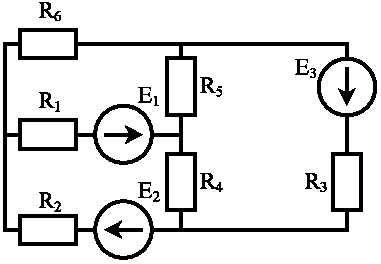
В соответствии с заданным вариантом из таблиц 1.1 и 1.2 выбираем схему и ее параметры.

Параметры элементов схемы.
r1= 5, Ом r2= 5, Ом r3=15, Ом r4=15, Ом r5=10, Ом r6=10, Ом	E1=15, В E2=20, В E3=30, В

Составим уравнения по второму закону Кирхгофа для контурных токов.

Решаем систему уравнений матричным методом (см. предыдущий пример).

Находим контурные токи.

Контурные токи найдены:

Ik₁=C₀ Ik₁=-0.722, A

Ik₂=C₁ Ik₂= 2.713, A

Ik₃=C₂ Ik₃= 1.948, A

Находим реальные токи.

Токи найдены:

I₁= 1.991, A

I₂= 2.713, A

I₃= 1.948, A

I₄= 0.765, A

I₅= 1.226, A

I₆=-0.722, A

Проверка баланса.

Pi =142.565, Вт

Pn=142.565, Вт

Баланс сошелся.

Потенциальные диаграммы.

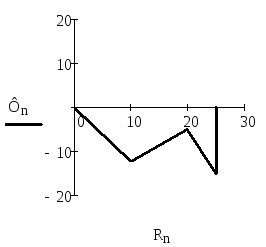
Контур 1

Ф0=0, В Ф1=-12.261, В Ф2=-5.043, В Ф3=-15.000, В Ф4=0, В

R0= 0, Ом R1=10, Ом R2=20, Ом R3=25, Ом R4=25, Ом

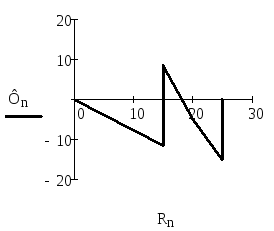
Контур 2

Ф0=0, В Ф1=-11.478, В Ф2=8.522, В Ф3=-5.043, В Ф4=-15, В Ф5=0, В

R0= 0, Ом R1=15, Ом R2=15, Ом R3=20, Ом R4=25, Ом R5=25, Ом

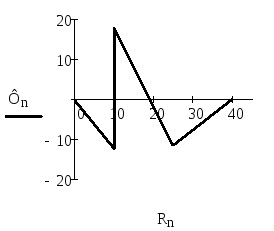
Контур 3

Ф0=0, В Ф1=-12.261, В Ф2=17.739, В Ф3=-11.478, В Ф4=0, В

R0= 0, Ом R1=10, Ом R2=20, Ом R3=25, Ом R4=40, Ом

Примечание: Построение потенциальных диаграмм можно выполнить либо в программе MathCAD, либо в ручную. При построении указать на диаграммах значению сопротивлений и потенциалов узлов.

3. Расчет методом узловых напряжений (потенциалов)

В соответствии с заданием из таблиц 1.1 и 1.2 выбираем схему и ее параметры.

Параметры элементов схемы.
r1= 0, Ом r2=10, Ом r3=15, Ом r4= 5, Ом r5=10, Ом r6=15, Ом	E1=15, В E2=25, В E3=30, В

Проводимости.

	g2=0.100, См
	g3=0.067, См		g4=0.200, См
	g5=0.100, См		g6=0.067, См

Уравнения по I закону Кирхгофа:

Выразим неизвестные токи ветвей через "условно известные" потенциалы узлов:

Подставим токи в уравнения по I закону Кирхгофа и перегруппируем:

Решаем полученную систему уравнений относительно потенциалов узлов, с помощью определителей.

	d = 0.084
	d1 = -0.733
	d2 = 0.133

Узловые потенциалы.

	Ф1=-8.684, В
	Ф3= 1.579, В

Подставляем полученные потенциалы в уравнении токов.

	I2= 0.842, A I3= 2.421, A I4=-1.737, A I5=-0.158, A I6= 0.684, A I1=-1.579, A

Проверка баланса.

Pn=117.386, Вт

Pi =117.386, Вт

Баланс сошелся.