10. Баланс мощностей.

Для любой замкнутой электрической цепи сумма мощностей Р_и, развиваемых источниками электрической энергии, равна сумме мощностей Р_п, расходуемых в приемниках

энергии :

 Р_и =  Р_п, или  (E_kI_k + U_kJ_k) =  I²_kR_k ,

где E_kI_k- алгебраическая сумма; здесь положительны те из слагаемых, для которых направления действия э.д.с. E_kи соответствующего тока I_kсовпадают, в противном случае слагаемое отрицательно;U_kJ_k- алгебраическая сумма; здесь положительны те из слагаемых, для которых напряжение на источнике тока (оно определяется расчетом цепи внешней по отношению к зажимам источника тока) и его ток J_kсовпадают по направлению, в противном случае слагаемое отрицательно;I²_kR_k- арифметическая сумма произведений; здесь должны быть учтены как внешние сопротивления, так и сопротивления самих источников энергии.

2. Краткая характеристика методов расчета электрических цепей

Наиболее универсальным методом анализа и расчёта электрических цепей является метод, основанный на применении IиII– го законов Кирхгофа.

Первый закон применяют для описания баланса токов в узлах электрической цепи, согласно которому: “Алгебраическая сумма токов, сходящихся в узле электрической цепи, должна быть равна нулю”:

Если бы условие (1.1) не выполнялось, то в узлах электрической цепи происходило бы накопление электрических зарядов, что экспериментально не подтверждается.

Второй закон применяют для описания замкнутых (условно или, безусловно) контуров, согласно которому: “Алгебраическая сумма ЭДС, действующих в замкнутом контуре, должна уравновешиваться алгебраической суммой падений напряжений на элементах замкнутого контура”:

Оба закона Кирхгофа являются следствиями закона сохранения энергии применительно к электрическим цепям.

Метод наложения (суперпозиции) применяют для анализа и расчёта только линейных электрических цепей, содержащих несколько источников энергии. Здесь токи в ветвях определяются путем алгебраического суммирования “частичных” токов, получающихся в ветвях под воздействием каждой частичной ЭДС схемы в отдельности.

Наиболее эффективен метод наложения тогда, когда в цепи содержатся источники тока (с R_ВН) и источники ЭДС (сR_ВН0), так как при рассмотрении “частичных” режимов работы схемы (только с каким – то одним источником) – идеальные источники ЭДС закорачиваются (из-заR_ВН0), а ветви с источником тока обрываются (из-заR_ВН), что вызывает максимальное упрощение схемы в конкретном “частичном” режиме.

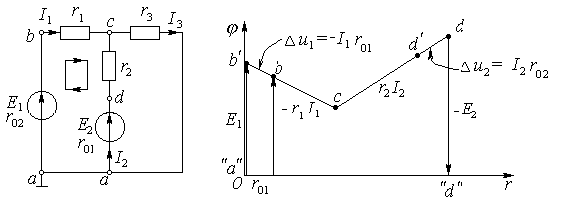
1. Потенциальная диаграмма.

Второй закон Кирхгофа наглядно иллюстрируется с помощью потенциальной диаграммы. Если по оси абсцисс прямоугольной системы координат отложить сопротивления участков в той последовательности, в которой они включены в цепь, а по оси ординат - потенциалы соответствующих точек, то получится график распределения потенциала вдоль неразветвленной цепи. Пользуясь этим графиком, можно определить напряжение между двумя любыми точками цепи. Порядок построения потенциальной диаграммы (предварительно необходимо выполнить расчет электрической цепи) состоит в следующем:

1). Выбираем опорный узел и принимаем его потенциал равным нулю;

2). Задаем положительное направление обхода контура;

3). Если направление обхода контура и направление тока совпадают на участке цепи, то потенциал при прохождении через сопротивление уменьшается (иначе - возрастает);

4). Идеальный источник э.д.с. вызывает скачкообразное изменение потенциала. Скачок потенциала положительный, если направление э.д.с. совпадает по направлению с обходом контура (иначе - отрицательный).

При построении ПД необходимо соблюдать следующие правила:

1.Если направление обхода выбранного замкнутого контура и направление тока на участке цепи совпадают, то потенциал будет уменьшаться при прохождении через сопротивление, на величину падения в нём напряжения.

2. Если направление обхода выбранного замкнутого контура и направление тока на участке цепи противоположны, то потенциал будет увеличиваться при прохождении через сопротивление, на величину падения в нём напряжения.

3.Идеальный источник ЭДС вызывает скачок потенциала на величину ЭДС источника (т.к. его R_ВН=0).

4.Скачок потенциала после источника ЭДС положительный, если направление ЭДС совпадает с направлением обхода и отрицательный, если направление ЭДС и направление обхода противоположны.

5.Источник ЭДС повышает потенциал в той точке, в которую направлена его стрелка.

Для примера построим потенциальную диаграмму для контура a-b-c-d-aв схеме представленной на рис. 13.

Примем потенциал точки “а” равным нулю (_a) и найдём последовательно потенциалы точекb,c,d:

_b = _a + E₁ – I₁r_01s ,

_c = _b - I₁r₁ = _a + E₁ – I₁r₀₁ - I₁r₁ ,

_d = _c + I₂r₂ = _a + E₁ – I₁r₀₁ - I₁r₁ + I₂r₂ ,

_a = _d – E₂ = 0.

а затем построим потенциальную диаграмму (рис. 13).

Рис. 13

Замечание.При построении ПД один из узлов схемы принимается за опорный и заземляется, т.е. его потенциал обнуляется. При этом токи в ветвях не изменяются, т.к. их величина зависит от разности потенциалов, а не от абсолютной величины потенциала одного отдельно взятого узла схемы.