Тема 13.5.Изоморфизм графов

Это отношение эквивалентности на множестве графов.

Определение: Изоморфным отображениемодного неориентированного графа на другой называется взаимооднозначное отображение вершин и дуг или рёбер одного графа – соответственно на вершины и дуги или рёбра другого графа, при котором сохраняется отношение инцидентности.

Пример 13.4:

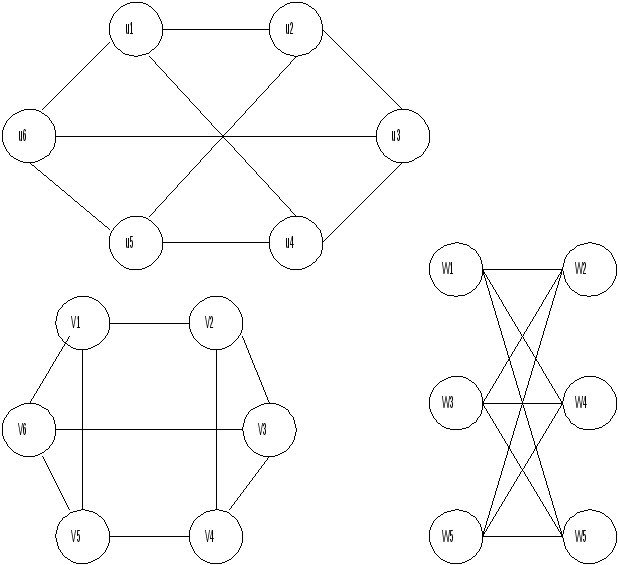
Графы – неизоморфны, а Графы– изоморфны.

Обычно изоморфные графы не различают. Число попарно неизоморфных графов с данным числом вершин и ребер конечно. Подобным же образом определяется изоморфизм ориентированных графов. Установление отношения изоморфности является важной проблемой теории графов. Для некоторых классов графов существуют эффективные алгоритмы, позволяющие установить изоморфизм.

Раздел 14. Проблемы достижимости на графах Тема 14.1.Граф достижимости

Один из первых вопросов, возникающих при изучении графов, это вопрос о существовании путей между заданными или всеми парами вершин. Ответом на этот вопрос – введённое выше отношение достижимости на вершинах графа вершинадостижима из вершины, еслиили весть путь изв. Иначе говоря, отношение достижимости является рефлексивным и транзитивным замыканием отношения. Для неориентированных графов это отношение также симметрично и, следовательно, является отношением эквивалентности на множестве вершин. В неориентированном графе классы эквивалентности по отношению достижимости называются связными компонентами. Для ориентированных графов достижимость, вообще говоря, не должна быть симметричным отношением. Симметричной является взаимная достижимость.

Определение:Вершиныиориентированного графаназываютсявзаимно достижимыми, если весть путь изви путь изв.

Ясно, что отношение взаимной достижимости является рефлексивным, симметричным и транзитивным и, следовательно, эквивалентностью на множестве вершин графа. Классы эквивалентности по отношению взаимной достижимости называются компонентами сильной связности или двусвязными компонентами графа.

Рассмотрим вначале вопрос о построении отношения достижимости. Определим для каждого графа его граф достижимости (называемый иногда также графом транзитивного замыкания), рёбра которого соответствуют путям исходного графа.

Определение:Пусть– ориентированный граф.Граф достижимостидляимеет тоже множество вершини следующее множество рёберв графевершинадостижима из вершины.

Пример 14.1:Рассмотрим граф.

Тогда можно проверить, что граф достижимости длявыглядит так (новые рёбра – петли для каждой из вершин не показаны):

Каким образом по графу можно построить граф? Один способ заключается в том, чтобы для каждой вершины графаопределить множество достижимых из неё вершин, последовательно добавляя в него вершины, достижимые из неё путями длины 0, 1, 2 и т.д.

Мы рассмотрим другой способ, основанный на использовании матрицы смежности графа и булевых операций.

Ниже для сохранения сходства с обычными операциями над матрицами мы будем использовать «арифметические» обозначения для булевых операций: через «+» будем обозначать дизъюнкцию , а через «*» конъюнкцию.

Обозначим через единичную матрицу размера, а- матрицу смежности заданного графа. Положим. Пусть,,…,. Наша процедура построенияоснована на следующем утверждении.

Лемма.Пусть Тогда

Доказательствопроведём индукцией по.

Базис. При иутверждение справедливо по определению.

Индукционный шаг. Пусть лемма справедлива для . Покажем, что она остаётся справедливой и для. По определениюимеем:

Предположим, что в графе извимеется путь длины. Рассмотрим кратчайший из таких путей. Если его длина, то по предположению индукции. Кроме того,. Поэтомуи. Если длина кратчайшего пути извравна, то пусть- его предпоследняя вершина. Тогда извимеется путь длиныи по предположению индукции. Так как, то. Поэтомуи.

Обратно, если , то хотя бы для одногослагаемоев сумме равно 1. Если это, тои по индуктивному предположению вимеется путь извдлины. Если же, тои. Это означает, что вимеетсяпутьизвдлиныиребро. Объединив их, получаемпутьизвдлины.

Из леммы непосредственно получаем

Следствие 1.Пусть – ориентированный граф с вершинами, а – его граф достижимости. Тогда .

Доказательство:Из леммы следует, что, если вимеется путь изв, то в нём имеется и простой путь извдлины. А по лемме все такие пути представлены в матрице.

Таким образом, процедура построения матрицы смежности графа достижимости длясводится к возведению матрицыв степень. Сделаем несколько замечаний, позволяющих упростить эту процедуру.

• Для возведения матрицы в произвольную степеньдостаточно выполнитьвозведений в квадрат:

где – это наименьшее число такое, что.

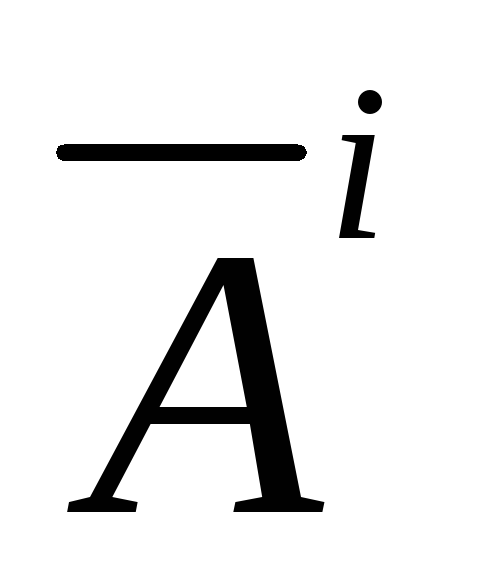• Так как на диагонали в матрице стоят единицы, то для любыхвсе единицы матрицысохраняются в матрице, в частности, и в матрице.

• Если при вычислении элемента 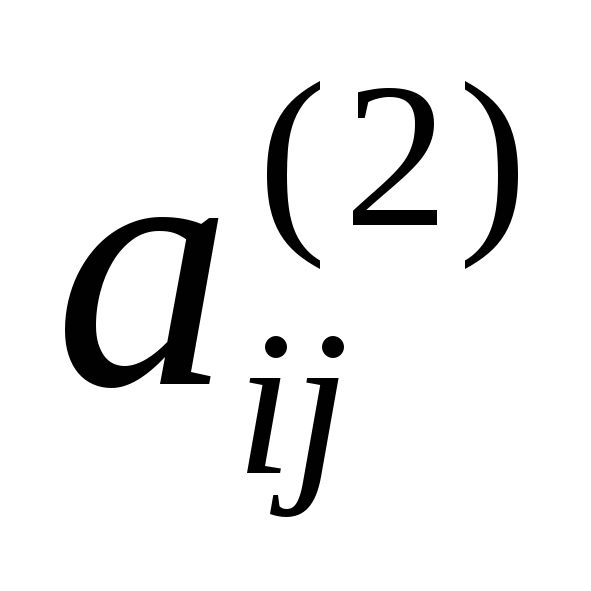матрицыпо стандартной формуле

обнаруживается такое , чтои, то и вся сумма. Поэтому остальные слагаемые можно не рассматривать.

Пример 14.2:Рассмотрим в качестве примера вычисление матрицы графа достижимостидля графапримера 14.1. В этом случае

Так как у имеется 6 вершин, то. Вычислим эту матрицу:

и . Таким образом,

Как видим, эта матрица действительно задаёт граф , представленный в примере 14.1.