
5семанглийскоеКалинина / третийкурс / величина / величинакалинина6
.rtf
любая
неубывающая, ограниченная сверху
последовательность имеет предел. Этот
предел и называют площадью фигуры
 при единице измерения длины
при единице измерения длины
 .
.
Обозначим
площадь фигуры
 символом
символом
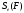 .
По определению
.
По определению
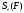 =
=
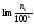 при
при
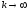 .
Т.е.
.
Т.е.
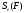 =
=
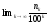
2.Обозначим
через
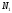 число квадратов первого ранга, задевающих
фигуру
число квадратов первого ранга, задевающих
фигуру
 (это
могут быть 1, 2, или 4 квадратных дециметра,
смотря по тому, как мы истолкуем границы
квадратов первого ранга на рисунках
9-11).
(это
могут быть 1, 2, или 4 квадратных дециметра,
смотря по тому, как мы истолкуем границы
квадратов первого ранга на рисунках
9-11).
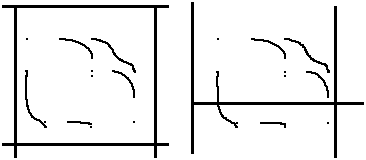
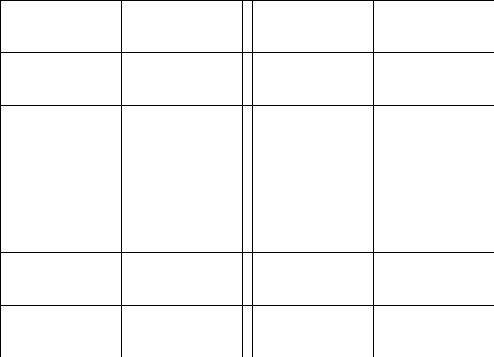
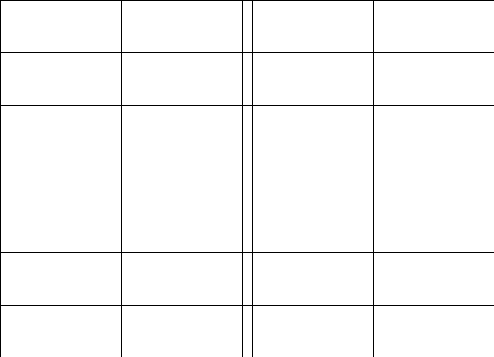
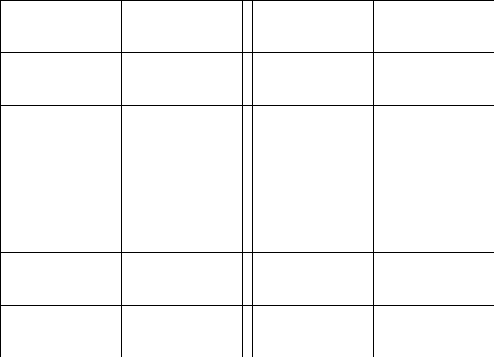
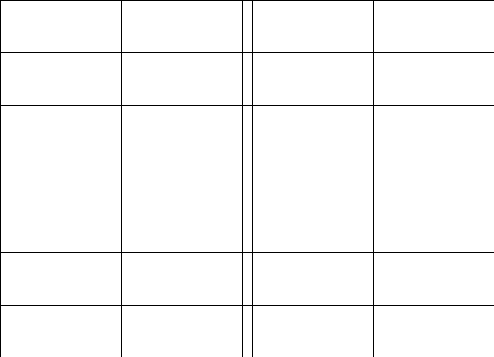
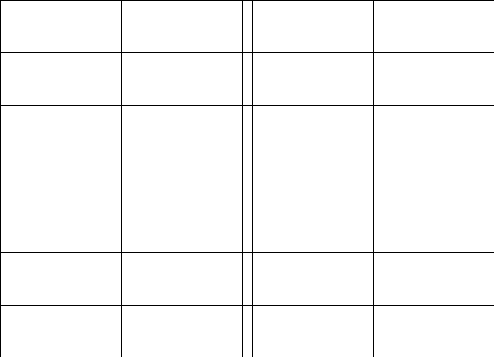
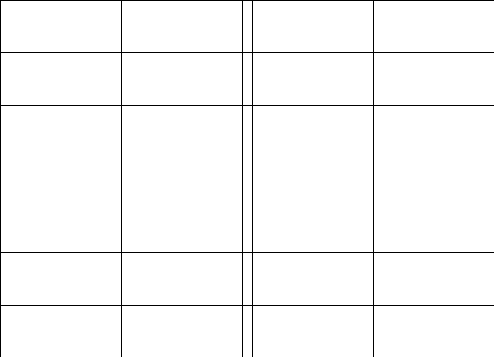
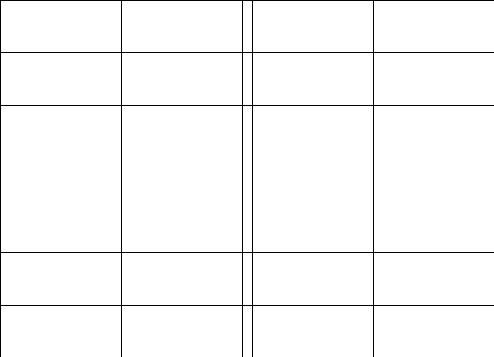
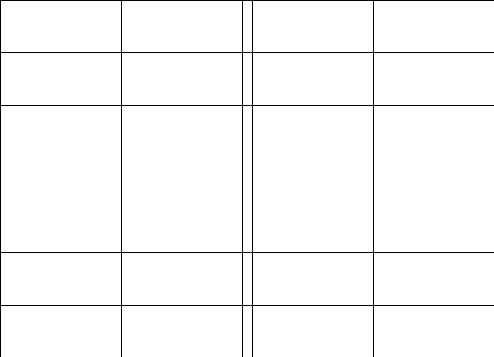
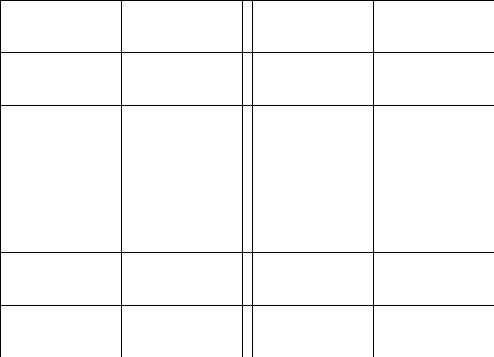
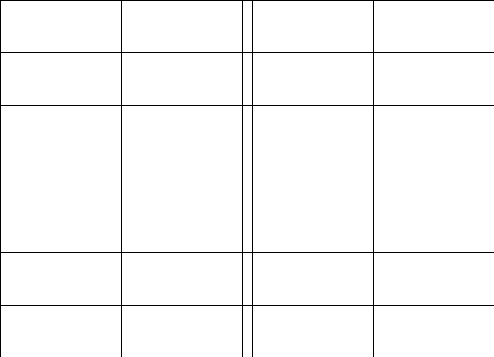
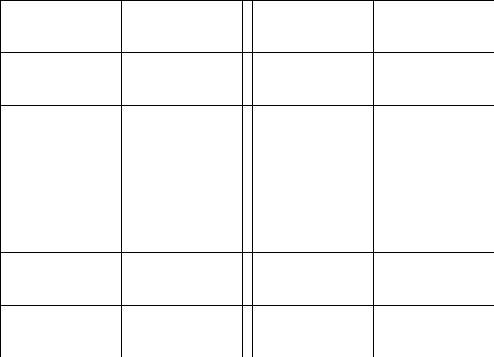
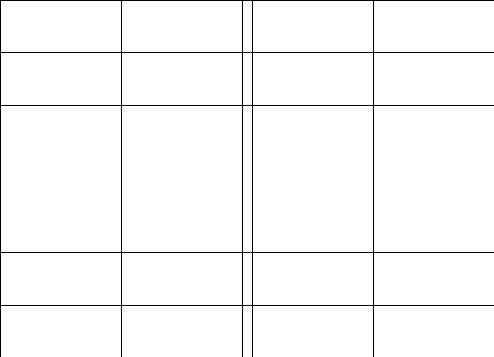
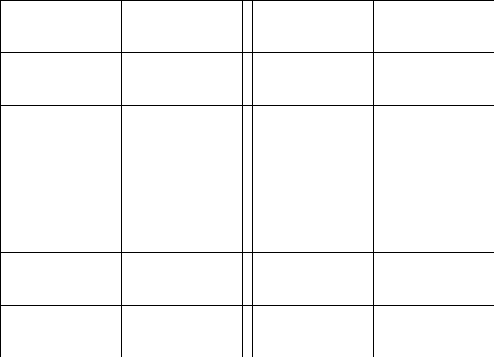
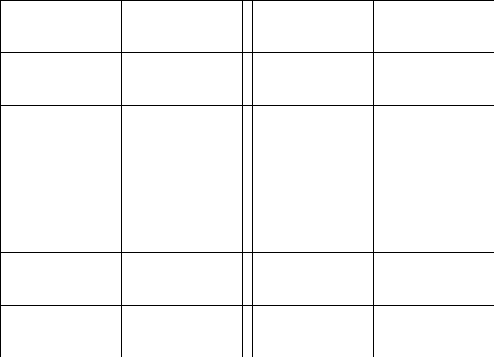
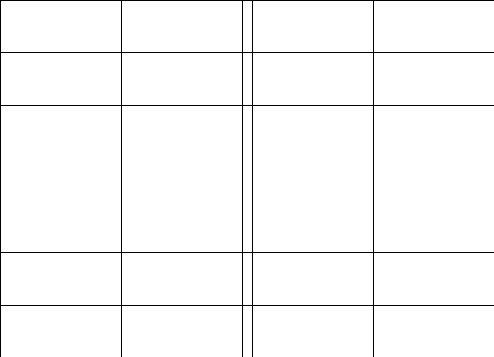
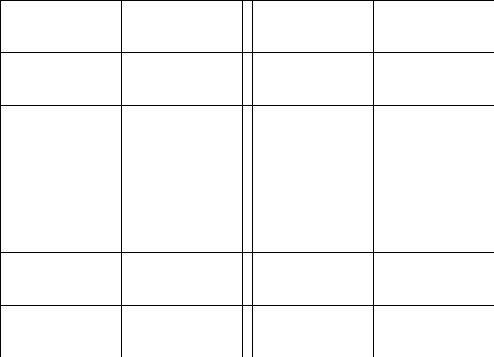
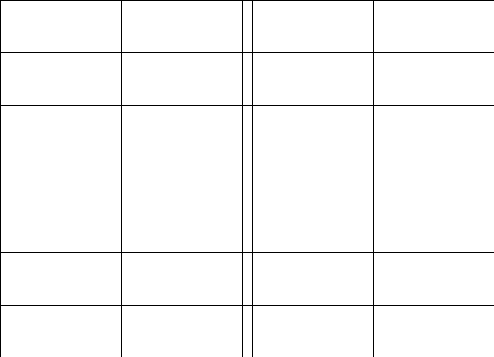
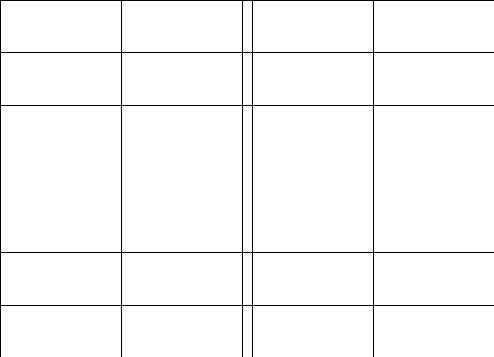
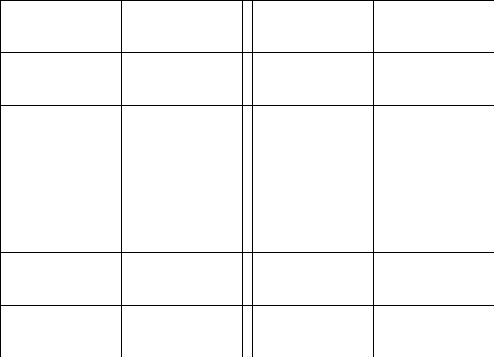
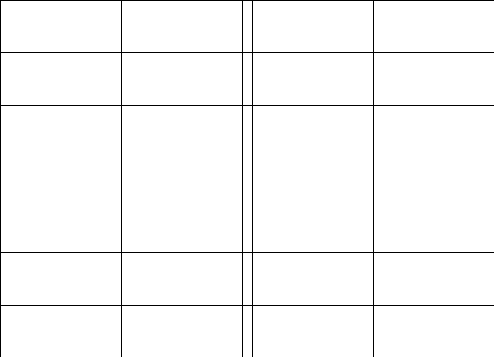
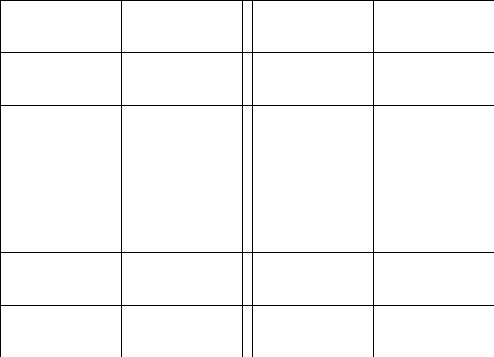
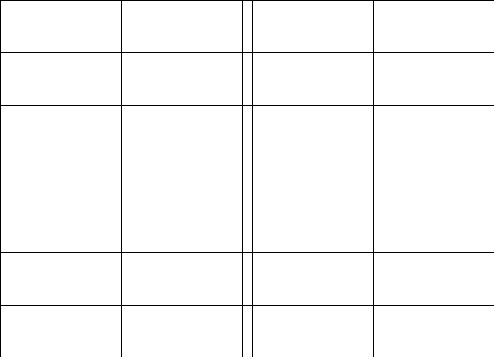
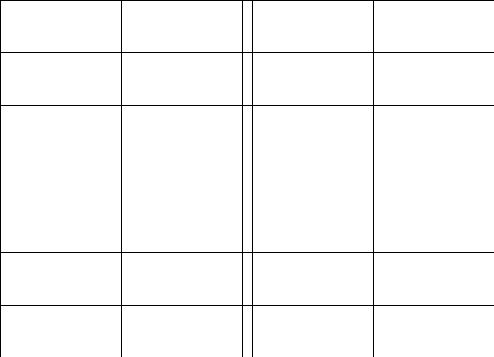
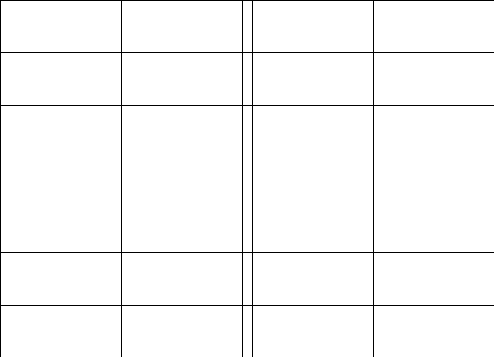
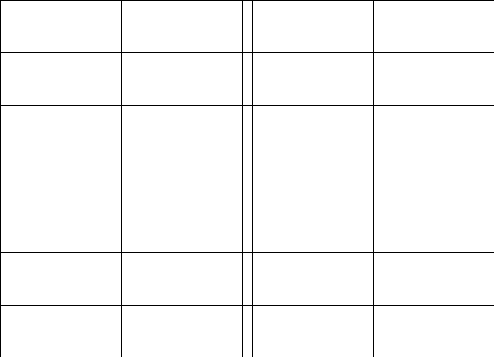
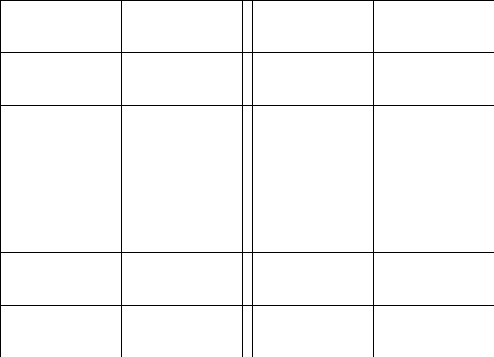
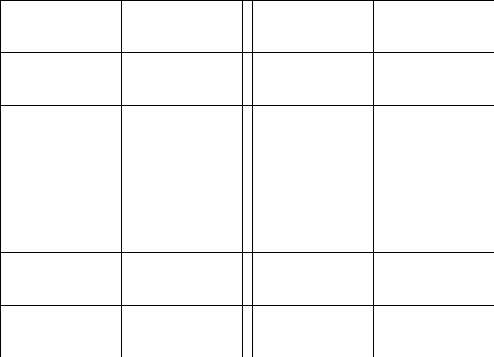
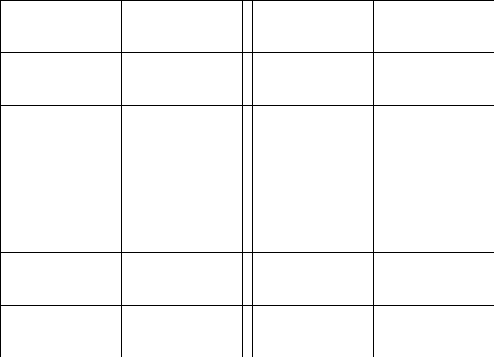
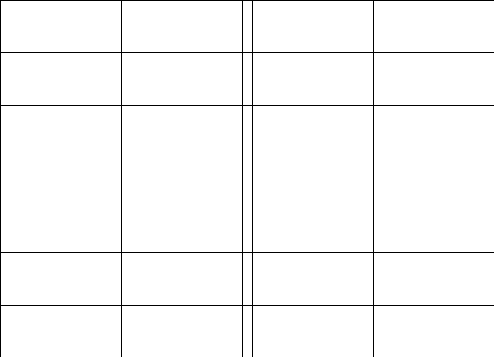
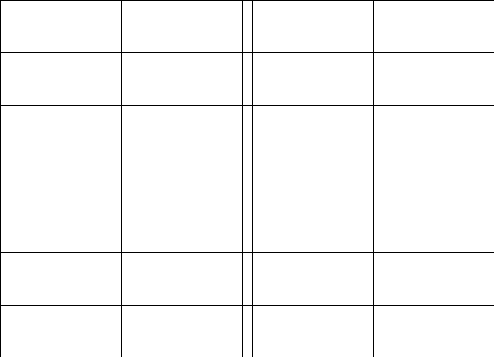
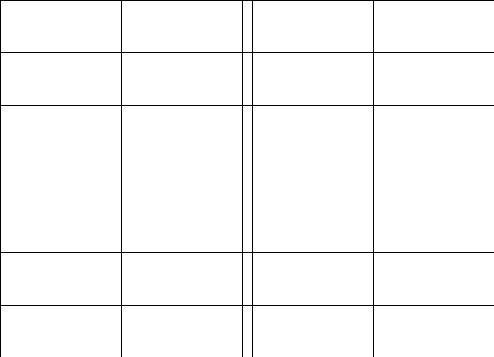
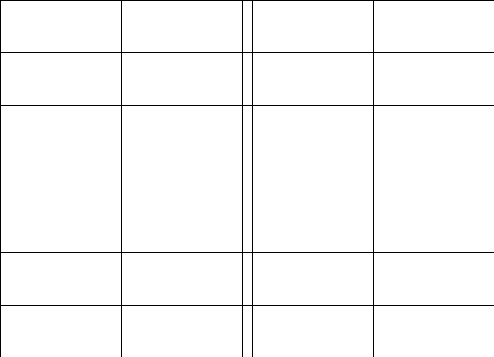
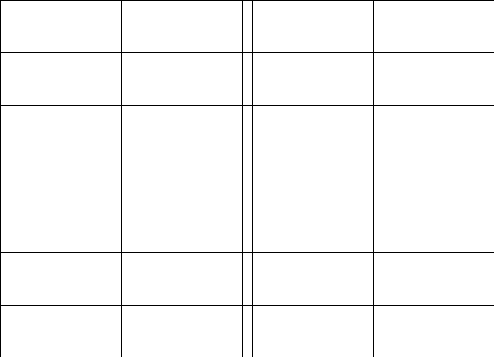
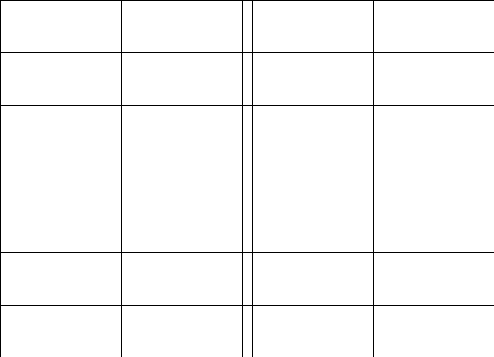
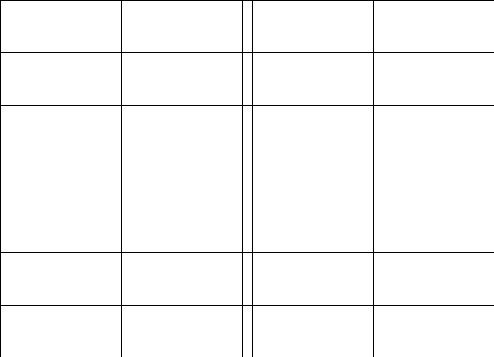
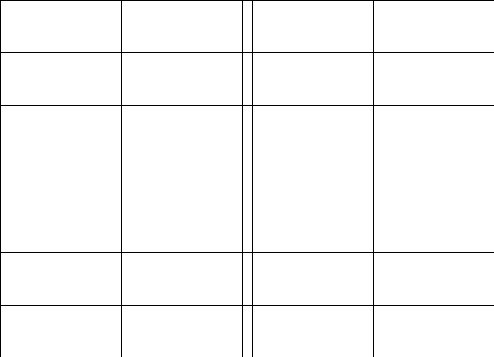
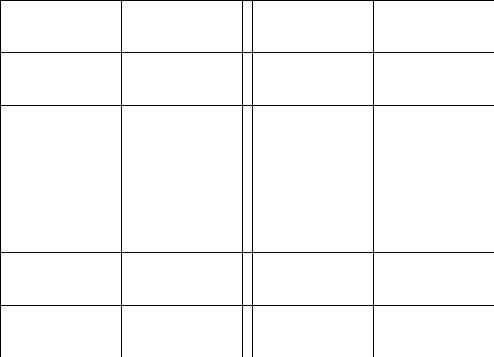
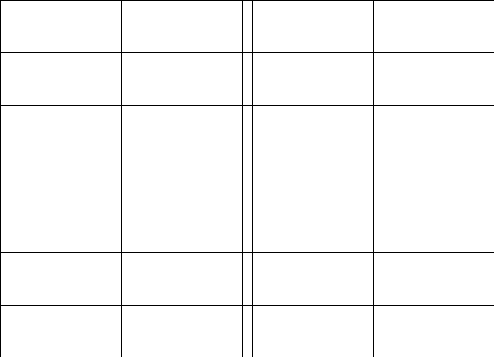
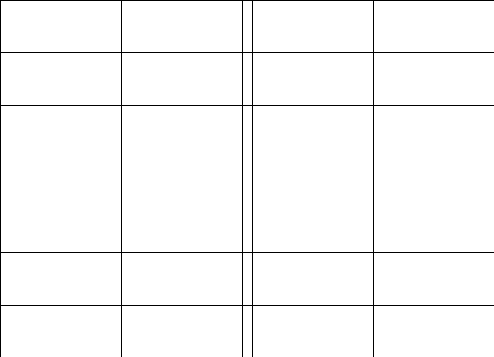
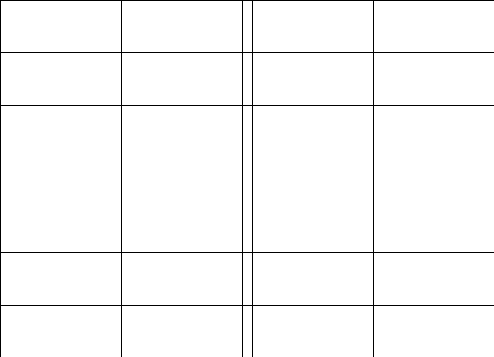
Рис. 9 Рис. 10
Обозначим
через
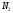 – число квадратов второго ранга,
задевающих фигуру
– число квадратов второго ранга,
задевающих фигуру
 (на рис.11 число
(на рис.11 число
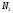 =53).
=53).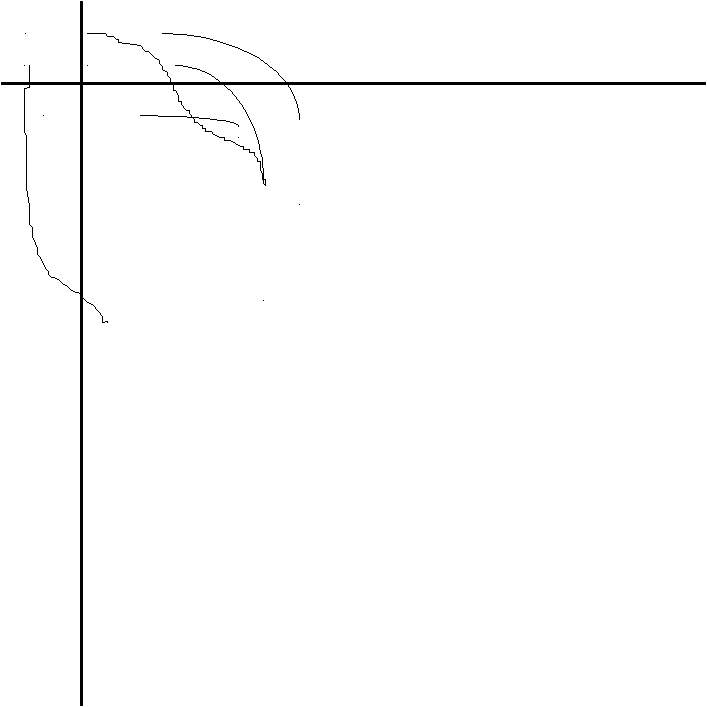
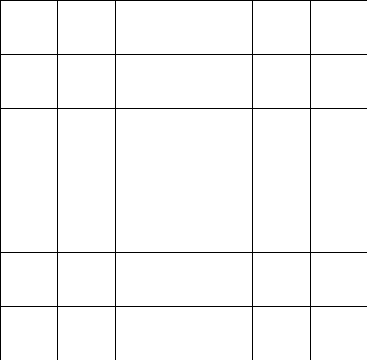



Рис. 11
И
т.д. Очевидно, что при любом натуральном
значении
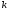 :
:
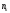

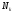 .
Рассмотрим бесконечную числовую
последовательность:
.
Рассмотрим бесконечную числовую
последовательность:
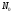 ;
;
 ;
;
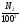 ;
...;
;
...;
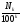 ;
...(2).
Можно
доказать, что эта последовательность
является невозрастающей и ограниченной
снизу, например, любым членом
последовательности (1), а потому имеет
предел:
;
...(2).
Можно
доказать, что эта последовательность
является невозрастающей и ограниченной
снизу, например, любым членом
последовательности (1), а потому имеет
предел:
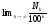 .
.
Покажем,
что для всех фигур, о которых идет речь,
этот предел совпадает с пределом
последовательности (1), т.е. также равен
площади фигуры
 .
При любом
.
При любом
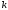 имеем:
имеем:
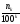

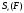

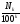 ,
а так как фигура
,
а так как фигура
 является квадрируемой фигурой, то
разность (
является квадрируемой фигурой, то
разность (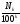 -
-
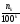 )
величина сколь угодно малая. Предел
этой разности при
)
величина сколь угодно малая. Предел
этой разности при
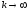 равен 0. Следовательно, пределы
последовательностей (1) и (2) совпадают:
равен 0. Следовательно, пределы
последовательностей (1) и (2) совпадают:
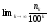 =
=
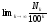 =
=
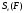
Таким
образом, площадь квадрируемой фигуры
 определяется как общий предел этих двух
последовательностей.
определяется как общий предел этих двух
последовательностей.
Замечание 1.
Пусть
фигура
 составлена из
составлена из
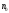 квадратов нулевого ранга. Тогда все
члены последовательности (1) равны числу
квадратов нулевого ранга. Тогда все
члены последовательности (1) равны числу
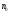 .
Действительно
.
Действительно
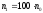 ,
а поэтому
,
а поэтому
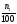 =
=
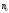 ,
аналогично
,
аналогично
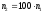 ,
т.е.
,
т.е.
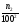 =
=
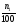 =
=
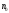 ,
и т.д. Отсюда следует, что в этом случае
предел последовательности (1) равен
числу
,
и т.д. Отсюда следует, что в этом случае
предел последовательности (1) равен
числу
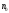 ,
т.е.
,
т.е.
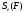 =
=
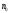 .
Теперь ясно, что площадь каждого квадрата
нулевого ранга равна 1.
.
Теперь ясно, что площадь каждого квадрата
нулевого ранга равна 1.
Если
же фигура
 составлена из
составлена из
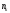 квадратов
квадратов
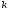 -го
ранга при некотором натуральном значении
-го
ранга при некотором натуральном значении
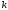 ,
то все члены последовательности (1),
начиная с (
,
то все члены последовательности (1),
начиная с (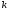 +1)-го,
равны числу
+1)-го,
равны числу
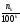 ,
а поэтому предел этой последовательности
равен
,
а поэтому предел этой последовательности
равен
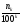 ,
т.е.
,
т.е.
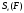 =
=
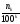 .
Отсюда следует, что площадь каждого
квадрата
.
Отсюда следует, что площадь каждого
квадрата
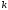 -го
ранга равна
-го
ранга равна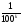 .
.
Замечание 2.
Числа
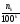 и
и
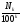 (площади многоугольников) можно
рассматривать как приближенные значения
площади фигуры
(площади многоугольников) можно
рассматривать как приближенные значения
площади фигуры
 ,
причем первое – с недостатком, а второе
– с избытком. Следует заметить, что эти
числа тем меньше отличаются от площади
,
причем первое – с недостатком, а второе
– с избытком. Следует заметить, что эти
числа тем меньше отличаются от площади
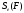 ,
чем больше
,
чем больше
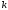 (рис.12 и рис.13)
(рис.12 и рис.13)
На
практике часто находят приближенное
значение площади фигуры как среднее
арифметическое чисел
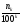 и
и
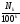 ,
причем это число тем ближе к площади
фигуры
,
причем это число тем ближе к площади
фигуры
 ,
чем больше
,
чем больше
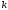 :
:
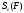
 (
(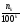 +
+
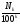 ):2
=
):2
=
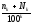 :2
:2
Числитель
этой дроби находят иногда иначе: ведь
каждый квадрат
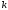 -го
ранга, лежащий внутри фигуры
-го
ранга, лежащий внутри фигуры
 ,
также и задевает фигуру
,
также и задевает фигуру
 ,
т.е.
,
т.е.
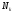 =
=
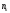 +
+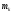 ,
где
,
где
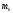 -
число квадратов
-
число квадратов
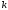 -го
ранга, задевающих фигуру
-го
ранга, задевающих фигуру
 ,
но не лежащих внутри нее. Отсюда:
,
но не лежащих внутри нее. Отсюда:
