10. Доверительный интервал для дисперсии нормально распределённой генеральной совокупности.

Предположим, что генеральная совокупность имеет нормальное распределение . Тогда случайная величина

(10.1)

имеет-распределение с числом степеней свободы . По таблице 4 -распределения можно найти , удовлетворяющее условию: (рис. 10.1).

Рис. 10.1

Рис. 10.2

По таблице -распределения всегда можно найти такие два числа и , которые удовлетворяли бы условию

. (10.2)

Таких пар чисел и существует бесконечное множество. Чтобы зафиксировать одну такую пару и , введём дополнительное условие (симметричность по вероятности): чтобы вероятности выхода величины за пределы интервала вправо и влево (заштрихованные площади на рис. 10.2) были одинаковы и равны

, т.е. . (10.3)

Из таблицы, используя условие (10.3), получаем . Для нахождения используем вероятность противоположного события

. (10.4)

Заменяя в формуле (10.2) его значением из формулы (10.1) и выполняя преобразования получаем

, (10.5)

где в скобках задан доверительный интервал для дисперсии .

Извлекая квадратный корень из обеих сторон неравенства, определяющего доверительный интервал для , получаем доверительный интервал для среднего квадратического отклонения :

. (10.6)

Таким образом, доверительный интервал для дисперсии нормального закона распределения имеет вид

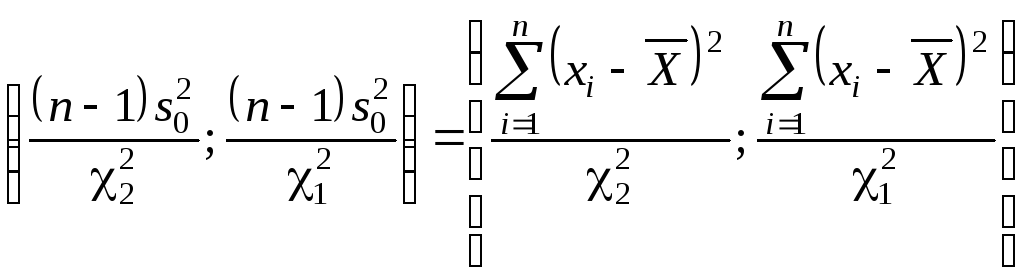. (10.7)

Пример 10.1. Произведено 12 измерений одним прибором (без систематической ошибки) некоторой физической величины, причём исправленное выборочное среднее квадратическое отклонение случайных ошибок измерений оказалось равным 0,6. Найти точность прибора с надёжностью , если результаты измерений распределены нормально.

Δ Точность прибора характеризуется средним квадратическим отклонением случайных ошибок измерений. Поэтому задача сводится к отысканию доверительного интервала, покрывающего с заданной надёжностью .

По данным и по таблице 4 найдём:

; .

Подставляя исходные данные в формулу (10.6), находим:

, т.е. .

Таким образом, с вероятностью . ▲

1 К. Пирсон (1857 – 1936) – английский математик.

2 Стьюдент – псевдоним английского статистика В.С. Госсета (1886 – 1937), открывшего это распределение в 1908 г.

14

© Гуров Владимир Владимирович, 2012