
- •Тема: Условная вероятность
- •Понятие условной вероятности.
- •Независимые события.
- •Формула полной вероятности.
- •Формула Байеса1.
- •Тема: Последовательность независимых испытаний
- •Биномиальное распределение вероятностей.
- •Наивероятнейшее число появлений события.
- •Предельные теоремы в схеме Бернулли. Распределение Пуассона.
- •Локальная предельная теорема Муавра – Лапласа.
- •Интегральная предельная теорема Муавра – Лапласа.
Тема: Условная вероятность
-
Понятие условной вероятности.
Вероятность события зависит от условий, при которых осуществляется опыт.
Пример 1.1. В семье два ребёнка: а) Какова вероятность того, что оба ребёнка – мальчики? б) Если известно, что один из детей – мальчик, то какова вероятность того, что оба ребёнка – мальчики? в) Известно, что старший ребёнок – мальчик. Какова вероятность того, что оба – мальчики?
D Обозначим: М – мальчик, Д – девочка. Событие ММ означает, что оба ребёнка – мальчики, причём старший мальчик – второй.
а) Пространство
элементарных событий
![]() и, значит,
и, значит,
![]() .
.
б) Элементарное
событие ДД
исключается, поэтому
![]() ,
и тогда
,
и тогда
![]() .
.
в) Имеем
![]() ,
т.е.
,
т.е.
![]() .
▲
.
▲
Этот пример показывает, что вероятность некоторого события существенно зависит от того, осуществились или нет некоторые условия.
Вероятность события
![]() при условии, что событие
при условии, что событие
![]() произошло, называется условной
вероятностью
события
произошло, называется условной
вероятностью
события
![]() и обозначается
и обозначается
![]() или
или
![]() .
Эта вероятность определяется равенством
.
Эта вероятность определяется равенством
![]() (1.1)
(1.1)
при условии, что
![]() .
.
Обоснуем формулу (1.1) в случае пространства событий с конечным числом исходов.
Пусть общее число
исходов равно
![]() ,
событию
,
событию
![]() благоприятствует
благоприятствует
![]() исходов, событию
исходов, событию
![]() –
–
![]() исходов, а совместному событию
исходов, а совместному событию
![]() –
–
![]() исходов. Тогда
исходов. Тогда
![]() ,
,
![]() .
Условная вероятность
.
Условная вероятность
![]() наступления события
наступления события
![]() при условии, что событие
при условии, что событие
![]() произошло, должна вычисляться не по
всем
произошло, должна вычисляться не по
всем
![]() исходам, а только по тем
исходам, а только по тем
![]() исходам, в результате которых наступило
событие
исходам, в результате которых наступило
событие
![]() ,
т.е.
,
т.е.
![]() .
.
Аналогично для
условной вероятности
![]() по формуле (1.1) имеем
по формуле (1.1) имеем
![]() ,
,
![]() .
(1.2)
.
(1.2)
Из равенств (1.1) и (1.2) получаем формулу умножения вероятностей:
![]() .
(1.3)
.
(1.3)
Пример 1.2. В коробке 3 красных и 7 синих шаров. Наугад извлекается один шар, затем второй. Найти вероятность того, что первый шар красный, а второй – синий.
D
Пусть событие
![]() означает, что первый взятый шар –
красный, а
означает, что первый взятый шар –
красный, а
![]() – что второй
шар синий. Тогда
– что второй
шар синий. Тогда
![]() .
Так как после извлечения красного в
коробке осталось 9 шаров, условная
вероятность
.
Так как после извлечения красного в
коробке осталось 9 шаров, условная
вероятность
![]() .
Тогда по формуле (1.3) искомая вероятность
.
Тогда по формуле (1.3) искомая вероятность
![]()
![]() .
▲
.
▲
Теорема
1.1
(умножения вероятностей). Для
произвольных событий
![]() справедлива формула
справедлива формула
![]()
![]() .
(1.4)
.
(1.4)
D
Докажем эту формулу для случая
![]() .
Согласно формуле (1.3), последовательно
будем иметь
.
Согласно формуле (1.3), последовательно
будем иметь
![]()
![]() .
▲
.
▲
Пример
1.3.
Кодовая
комбинация состоит из 10 импульсов трёх
форм:
![]() ,
,
![]() и
и
![]() ,
причём в каждой кодовой комбинации 3
импульса имеют форму
,
причём в каждой кодовой комбинации 3
импульса имеют форму
![]() ,
2 импульса – форму
,
2 импульса – форму
![]() ,
5 импульсов – форму
,
5 импульсов – форму
![]() .
Найти вероятность прихода первых трёх
импульсов в последовательности
.
Найти вероятность прихода первых трёх
импульсов в последовательности
![]() .
.
D Согласно формуле (1.4), искомая вероятность
![]() .
.
По условию
![]() ,
,
![]() ,
так как импульс
,
так как импульс
![]() уже пришёл и осталось 9 возможностей
для двух импульсов формы
уже пришёл и осталось 9 возможностей
для двух импульсов формы
![]() .
Далее
.
Далее
![]() ,
так как импульсы
,
так как импульсы
![]() и
и
![]() пришли и для 5 импульсов формы
пришли и для 5 импульсов формы
![]() осталось 8 возможностей. Таким образом,
осталось 8 возможностей. Таким образом,
![]() .
▲
.
▲
-
Независимые события.
События
![]() и
и
![]() называются независимыми,
если появление одного из них не меняет
вероятности появления другого, т.е.
называются независимыми,
если появление одного из них не меняет
вероятности появления другого, т.е.
![]() или
или
![]() .
(2.1)
.
(2.1)
Для двух независимых событий формула умножения вероятностей принимает вид
![]() ,
(2.2)
,
(2.2)
т.е. вероятность произведения двух независимых событий равна произведению вероятностей этих событий.
Если
![]() и
и
![]() независимые события, то независимы
также события: а)
независимые события, то независимы
также события: а)
![]() и
и![]() ;
б)
;
б)
![]() и
и
![]() ;
в)
;
в)
![]() и
и
![]() .
.
Докажем, например,
независимость событий
![]() и
и
![]() .
В самом деле, если
.
В самом деле, если
![]() и
и
![]() независимы, то
независимы, то
![]() .
Так как
.
Так как
![]()
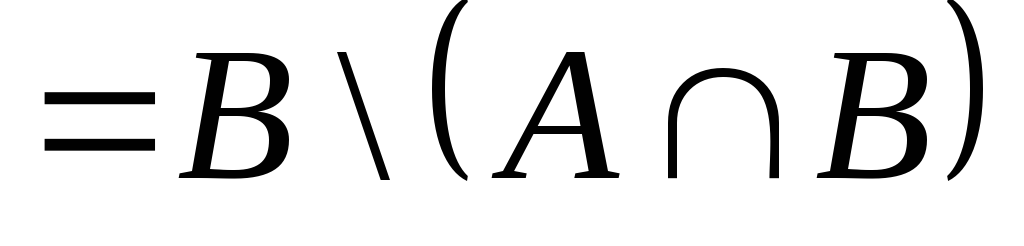 ,
то
,
то
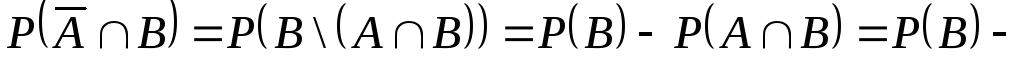
![]() ,
т.е.
,
т.е.
![]() и
и
![]() независимые события.
независимые события.
События
![]() называются попарно
независимыми,
если любая пара их независима, т.е.
называются попарно
независимыми,
если любая пара их независима, т.е.
![]() ,
,
![]() .
События
.
События
![]() называются независимыми
в совокупности,
если при любом выборе различных событий
называются независимыми
в совокупности,
если при любом выборе различных событий
![]() из данной совокупности выполняется
равенство
из данной совокупности выполняется
равенство
![]() .
(2.3)
.
(2.3)
Ясно, что из независимости событий в совокупности следует их попарная независимость. Однако попарная независимость событий не гарантирует их независимости в совокупности.
Если события
![]() независимы в совокупности, то из
определения (2.3) получаем равенство
независимы в совокупности, то из
определения (2.3) получаем равенство
![]() ,
(2.4)
,
(2.4)
обобщающее формулу (2.2).
Из формул (2.4) и
(4.6) (Тема: Вероятность события) следует
утверждение: вероятность появления
хотя бы одного события
![]() из независимых в совокупности событий
из независимых в совокупности событий
![]()
![]() .
(2.5)
.
(2.5)
Пример
2.1.
Вероятность
попадания в цель из трёх винтовок
![]() ;
;
![]() ;
;
![]() соответственно, где
соответственно, где
![]() – попадание
в мишень
– попадание
в мишень
![]() -м
стрелком,
-м
стрелком,
![]() .
Найти вероятность: а) хотя бы одного
попадания; б) только одного попадания.
.
Найти вероятность: а) хотя бы одного
попадания; б) только одного попадания.
D
а) Попадание в цель из каждой винтовки
не зависит от результата стрельбы из
других винтовок, т.е. стрельба из винтовок
– независимые в совокупности события.
Промах является событием, противоположным
попаданию. Для этих винтовок вероятности
промаха
![]() ;
;
![]() ;
;
![]() соответственно. Тогда, согласно равенству
(2.5), искомая вероятность
соответственно. Тогда, согласно равенству
(2.5), искомая вероятность
![]() .
.
б) Только одно
попадание в мишень может осуществиться
в одной из трёх ситуаций: 1) 1-й стрелок
поразил цель, 2-й и 3-й стрелки промахнулись
– событие
![]() ;
2) 2-й стрелок попал, а 1-й и 3-й промахнулись
– событие
;
2) 2-й стрелок попал, а 1-й и 3-й промахнулись
– событие
![]() ;
3) 1-й и 2-й стрелки промахнулись, а третий
попал –
событие
;
3) 1-й и 2-й стрелки промахнулись, а третий
попал –
событие
![]() .
События
.
События
![]() ,
,
![]() и
и
![]() несовместны. Тогда искомая вероятность
попадания в мишень только одним стрелком
несовместны. Тогда искомая вероятность
попадания в мишень только одним стрелком
![]()
![]()
![]() .
▲
.
▲
