-
Формула полной вероятности.
Пусть события
попарно независимы и образуют полную
группу событий, т.е.
.
Такие события иногда называют гипотезами.
Имеет место
Теорема
3.1
(о полной вероятности). Вероятность
события
,
которое может наступить лишь при
появлении одного из несовместных событий
,
образующих полную группу событий, равна
сумме произведений вероятностей каждой
из гипотез на соответствующую условную
вероятность события
,
т.е.
.
(3.1)
Равенство (3.1) называется формулой полной вероятности.
D
Так как
,
то
,
причём события
попарно несовместны в силу попарной
несовместности гипотез
,
.
Тогда по формуле (4.2) (Тема: Вероятность
события)
.
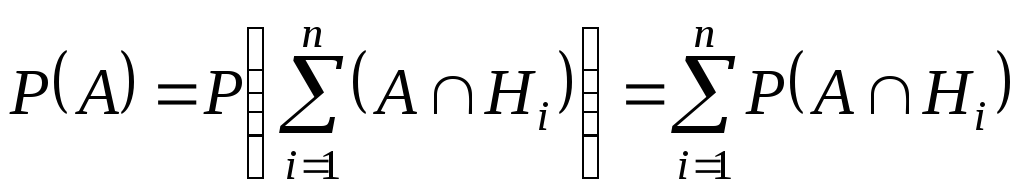Применив к каждому слагаемому в правой части формулу (1.3), получим равенство
,
совпадающее с равенством (3.1). ▲
Пример 3.1. В лаборатории имеется 6 мини-ЭВМ и 4 микрокалькулятора. Вероятность того, что во время выполнения расчёта мини-ЭВМ не выйдет из строя, равна 0,95, для микрокалькулятора эта вероятность равна 0,8. Найти вероятность того, что взятое наугад вычислительное устройство не выйдет из строя до окончания расчёта.
D
Пусть
– событие,
состоящее в том, что вычислительное
устройство не выйдет из строя. Это
событие может произойти с одной из
гипотез:
– взята
мини-ЭВМ,
– взят
микрокалькулятор. Тогда
,
и по условию задачи
,
.
По формуле полной вероятности искомая
вероятность
.
▲
-
Формула Байеса1.
С формулой полной
вероятности тесно связана формула
Байеса. Она даёт возможность определить
условные апостериорные
(после опыта) вероятности
,
,
если известны априорные
(до опыта) вероятности
гипотез
,
образующих полную группу событий. Эта
формула имеет вид
,
.
(4.1)
Для её вывода
достаточно в формуле условной вероятности
записать числитель по формуле произведения
вероятностей (1.3), а знаменатель – по
формуле полной вероятности (3.1).
Пример 4.1. В канцелярии работают 4 секретарши, которые отправляют 40, 10, 30 и 20 % исходящих бумаг. Вероятности неверной адресации бумаг секретаршами равны 0,01; 0,04; 0,06 и 0,01 соответственно. Найти вероятность того, что документ, неверно адресованный, отправлен третьей секретаршей.
D
Введём гипотезы
– документ
отправила
-я
секретарша,
.
Тогда по условию задачи
;
;
;
.
Обозначим через
событие, состоящее в том, что документ
адресован неверно. Тогда по условию
;
;
;
и искомая вероятность
.
Итак, 3-я секретарша допускает примерно 39 % всех ошибок. ▲
Тема: Последовательность независимых испытаний
-
Схема испытаний Бернулли.
Пусть производится
серия из
испытаний, в каждом из которых может
произойти или не произойти событие
.
При этом представляет интерес исход не
каждого отдельного испытания, а общее
число появления события
в результате определённого числа опытов.
Последовательные
испытания называются независимыми,
если вероятность осуществления любого
исхода в каждом
-м
испытании не зависит от реализации
исходов предыдущих испытаний. Легко
представить испытания с двумя возможными
исходами
и
,
где
означает, например, «успех», а
– «неудачу»,
причём в каждом испытании вероятность
«успеха» и вероятность
«неудачи» постоянны. Серию независимых
испытаний с одной и той же вероятностью
«успеха»
называют испытаниями
или схемой
Бернулли.
Обозначим через
вероятность появления
раз события
в серии из
независимых испытаний. Тогда справедлива
формула
Бернулли
.
(1.1)
D
Действительно, вероятность того, что
при
испытаниях событие
наступит
раз и, следовательно, не появится
раз, согласно формуле (2.4) (Тема_02) умножения
вероятностей событий, равна
.
Но событие
может наступить при любом
из
возможных испытаний. Так как число
возможных комбинаций
элементов из
равно
,
а комбинации между собой несовместны,
то по формуле (4.2) (Тема_01) искомая
вероятность
.
▲
Пример
1.1.
Производится
4 выстрела по мишени. Вероятность
попадания при каждом выстреле
.
Найти вероятность двух попаданий.
D
Стрельба по мишени есть последовательность
независимых опытов (выстрелов) с
постоянными вероятностями попадания
и непопадания
при каждом выстреле.
По формуле Бернулли
.
▲