Тема: Числовые характеристики скалярных случайных величин
К числовым характеристикам с.в. относятся: математическое ожидание, дисперсия, моменты различных порядков и т.д.
-
Математическое ожидание.
Пусть
– дискретная с.в., принимающая значения
с вероятностями
соответственно.
Математическим
ожиданием
(м.о.) или средним
значением
с.в.
называется число
(1.1)
в предположении, что этот ряд сходится абсолютно.
Если же ряд
расходится, то говорят, что с.в.
не имеет конечного м.о.
Если
– непрерывная с.в. с плотностью вероятности
,
то её м.о. определяется интегралом
(1.2)
при условии, что он сходится абсолютно.
Пусть
– дискретная с.в. с законом распределения
(2.1) (Тема: Скалярные случайные величины),
а
– функция этой с.в. Тогда закон
распределения с.в.
имеет вид табл. 7.1 (Тема: Скалярные
случайные величины). Согласно равенству
(1.1), м.о. случайной величины
определяется формулой
.
Если же
– непрерывная с.в. с плотностью вероятности
,
то, обобщая предыдущие рассуждения,
получаем формулу для м.о. случайной
величины
в виде
.
(1.3)
Пример 1.1. В денежной лотерее выпущено 200 билетов. Разыгрывается один выигрыш в размере 50 руб., два – по 25 руб., десять – по 1 руб. Найти среднюю величину выигрыша, если куплен один билет.
D
Согласно примеру 2.1 (Тема:
Скалярные случайные величины),
закон распределения с.в.
– выигрыша – имеет вид (2.2) (Тема: Скалярные
случайные величины).
По формуле (1.1) средняя величина выигрыша
(руб.)
Итак, средний выигрыш в лотерее равен 55 коп. ▲
Пример
1.2.
Плотность
распределения вероятностей с.в.
имеет вид
Найти
.
D
По формуле (1.3)
.
▲
Выясним основные свойства математического ожидания.
10.
М.о. числа появлений события
в одном испытании равно вероятности
этого события.
20.
М.о. постоянной неслучайной величины
равно
.
30.
Постоянный неслучайный множитель
можно выносить за знак математического
ожидания.
40.
Для любых случайных величин (зависимых
или независимых) м.о. суммы с.в.
и
равно сумме м.о. этих величин:
.
(1.4)
50.
Для независимых случайных величин м.о.
произведения с.в.
и
равно произведению м.о. этих с.в., т.е.
.
(1.7)
Пример 1.3. Найти м.о. суммы числа очков, которые могут выпасть при бросании двух игральных костей.
D
Пусть
и
– число выпавших очков на первой и
второй кости соответственно. Дискретные
с.в.
и
принимают значения 1, 2, 3, 4, 5 и 6 с одинаковой
вероятностью
.
Тогда по формулам (1.4) и (1.1) искомое м.о.
.
▲
-
Дисперсия.
М.о. характеризует
среднее значение с.в. Отклонением
с.в.
от своего математического ожидания
(среднего значения) называется с.в.
.
Часто величина
называется центрированной
с.в.
Дисперсией
или рассеянием
случайной величины
называется математическое ожидание
квадрата отклонения случайной величины
от её математического ожидания:
.
(2.1)
Корень квадратный
из дисперсии называется средним
квадратическим
(квадратичным)
отклонением с.в.
и обозначается
,
так что
.
Для дискретной
с.в.
,
принимающей значения
с вероятностью
,
,
дисперсия определяется равенством
,
(2.2)
где
.
Для непрерывной
с.в.
дисперсия определяется равенством
,
(2.3)
если этот интеграл
существует. Здесь
– плотность вероятности с.в.
.
Из свойств м.о. и определения дисперсии имеем
.
Итак, для дискретной
с.в.
.
(2.4)
Для непрерывной
с.в.
равенство (2.4) имеет вид
.
(2.5)
Формулы (2.4) и (2.5) более удобны для вычисления дисперсии.
Замечание.
Из определения дисперсии (2.1) с.в.
следует, что
.
Если дисперсия мала, то каждый член
суммы (2.2) тоже мал. Следовательно,
значение
,
при котором
велико, должно иметь малую вероятность.
Другими словами, при малой дисперсии
большие отклонения с.в.
от её м.о.
маловероятны. Равенство
означает, что
для тех значений
,
вероятность
которых равна нулю. Иначе говоря,
означает, что
с вероятностью, равной единице.
Пример
2.1.
Найти дисперсию с.в.
,
заданной законом распределения
вероятностей
|
|
|
|
|
|
|
|
|
|
D
Находим м.о.:
.
Так как закон распределения с.в.
имеет вид
|
|
|
|
|
|
|
|
|
|
то
,
и по формуле (2.4)
.
▲
Пример
2.2.
Найти дисперсию с.в.
,
функция распределения которой
D Находим плотность вероятности
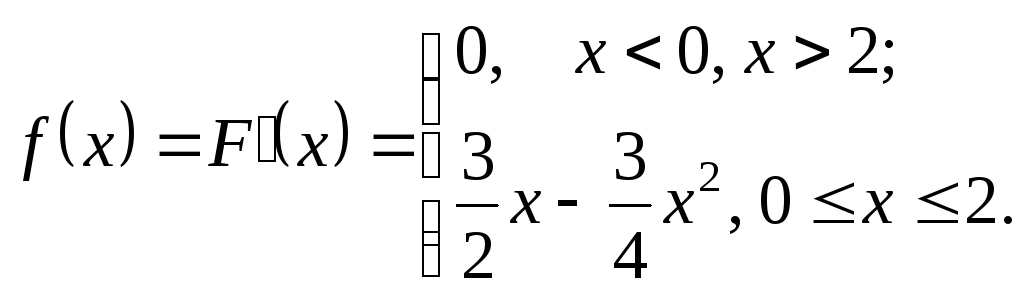
Далее,
;
.
По формуле (2.5) искомая дисперсия
.
▲
Установим свойства дисперсии.
10. Дисперсия постоянной неслучайной величины равна нулю.
Действительно,
.
20.
Постоянный неслучайный множитель
можно выносить за знак дисперсии, возводя
его в квадрат:
.
В самом деле,
.
30.
Дисперсия суммы или разности независимых
с.в.
и
равна сумме дисперсий этих величин:
.
D
Так как
и
независимые с.в., то
и, следовательно,
.
Итак,
.
Отсюда и из свойства 20
дисперсии получим
.
▲