5. Моменты случайной величины.

Математическое ожидание случайной величины есть её среднее значение, в физическом смысле оно определяет центр тяжести графика закона распределения или плотности; дисперсия характеризует разброс с.в. относительно её среднего значения; мода и медиана характеризуют положение с.в. Кроме этих величин, для более детальной характеристики с.в. вводятся моменты с.в. различных порядков, начальные и центральные.

Начальным моментом -го порядка с.в. называется м.о. величины :

, . (5.1)

При получаем , т.е. математическое ожидание с.в. есть начальный момент первого порядка.

Из определения математического ожидания с.в. следует, что начальный момент -го порядка (5.1) определяется:

для дискретной с.в. равенством

, (5.2)

а для непрерывной с.в. равенством

, (5.3)

где – плотность вероятности с.в. .

Центральным моментом -го порядка называется м.о. величины , т.е.

, . (5.4)

Отсюда следует, что , , , т.е. второй центральный момент с.в. равен дисперсии этой с.в.

Из определения математического ожидания с.в. следует, что центральный момент -го порядка (5.4) для дискретной с.в. определяется равенством

, , (5.5)

а для непрерывной с.в. – равенством

, (5.6)

где – плотность вероятности с.в. .

Получим соотношения между начальными и центральными моментами различных порядков.

Так как , то из равенства (5.6) имеем

,

т.е.

, .

Отсюда последовательно имеем

;

;

;

;

;

………………………………………………………………..

Тема: Закон больших чисел. Предельные теоремы теории вероятностей

1. Закон больших чисел.

Закон больших чисел имеет несколько форм, каждая из которых устанавливает ту или иную устойчивость средних при большом числе наблюдений.

1) Неравенство Чебышева. Если с.в. имеет конечный первый абсолютный момент , то при любом

. (1.1)

В частности, если и существует , то справедливо первое неравенство Чебышева:

. (1.2)

Если существует , то при любом справедливо второе неравенство Чебышева:

. (1.3)

Если в неравенстве Чебышева (1.3) вместо положить , то, учитывая, что , придём ко второму неравенству Чебышева в центрированной форме

. (1.4)

Если рассмотреть событие , противоположное событию , то из неравенства (1.4) получим другую его форму

. (1.5)

Неравенство (1.5) подчёркивает уместность выбора дисперсии в качестве меры рассеяния значений с.в. от м.о. В самом деле, как следует из неравенства (1.5), чем меньше дисперсия , тем при меньшем значении можно с той же оценкой вероятности утверждать, что значения с.в. будут концентрироваться ближе к .

Положив в неравенстве (1.5) , получим

,

т.е. вероятность того, что произвольная с.в. отклонится от своего м.о. меньше, чем на утроенное среднеквадратическое отклонение, не меньше . Это утверждение носит название «правила трёх сигм». В частности, для нормального распределения с.в. по закону «правило трёх сигм» даёт оценку .

Пример 1.1. При изготовлении партии одинаковых деталей размерами существует допуск . Оценить вероятность того, что взятая случайно деталь бракована, если .

D Пусть – размеры детали. По условию ; ; . Требуется оценить вероятность . По неравенству Чебышева (1.4) , т.е. искомая вероятность не превышает 0,25. ▲

Рассмотрим последовательность случайных величин . Что понимать под пределом такой последовательности? Существуют различные определения предела для последовательности с.в. . Рассмотрим некоторые из них.

Если событие имеет вероятность, равную единице, то будем писать при и говорить, что последовательность сходится к пределу с вероятностью 1.

Если математическое ожидание при , то говорят, что последовательность сходится к в среднеквадратическом смысле.

Если же для всех при

, (1.6)

то будем говорить, что последовательность сходится к по вероятности и писать

. (1.7)

2) Теорема Чебышева (закон больших чисел). Из неравенства Чебышева (1.4) и определения (1.6) сходимости по вероятности вытекает следующая

Лемма. Если для последовательности случайных величин выполнены равенства , , то сходится по вероятности к , т.е. .

Отсюда получаем следующее утверждение.

Теорема 1.1 (Чебышева). Пусть – последовательность попарно независимых случайных величин, дисперсии которых ограничены в совокупности одним и тем же числом , т.е. , , . Тогда последовательность случайных величин

сходится по вероятности к нулю при , т.е.

(1.8)

или

. (1.9)

Перепишем в виде

.

Тогда теорему Чебышева можно записать в виде

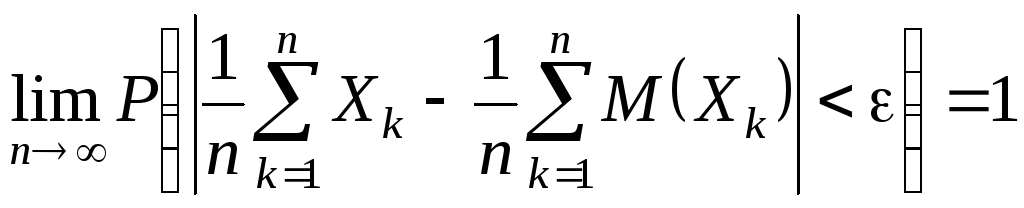. (1.10)

Величина называется средним арифметическим с.в. , .

Обобщением теоремы Чебышева является

Теорема 1.2 (Хинчина¹). Среднее арифметическое одинаково распределённых независимых случайных величин , имеющих конечное математическое ожидание , , при неограниченном возрастании стремится по вероятности к числу :

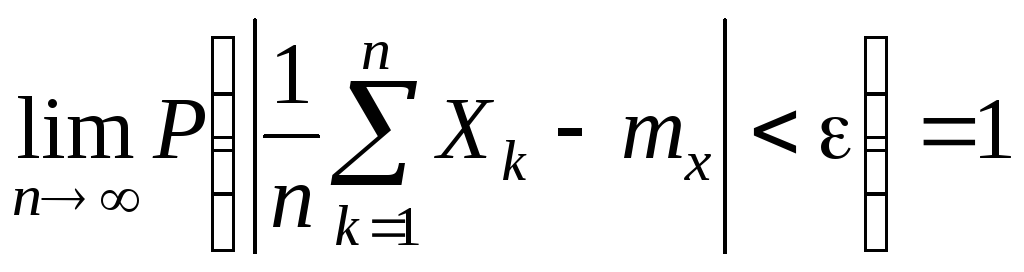, (1.11)

где – любое положительное число.

Эта теорема, приводимая без доказательства, служит обоснованием правила среднего арифметического в теории измерений: при достаточно большом количестве измерений некоторой случайной величины за приближённое её значение принимается среднее арифметическое этих измерений.

Теорема 1.3 (Бернулли). При неограниченном увеличении числа независимых испытаний в постоянных условиях относительная частота появлений события сходится по вероятности к вероятности появления события в одном испытании, т.е.

, (1.12)

где – число появлений события при испытаниях.

Теорема Бернулли подтверждает обоснованность статистического определения вероятности.