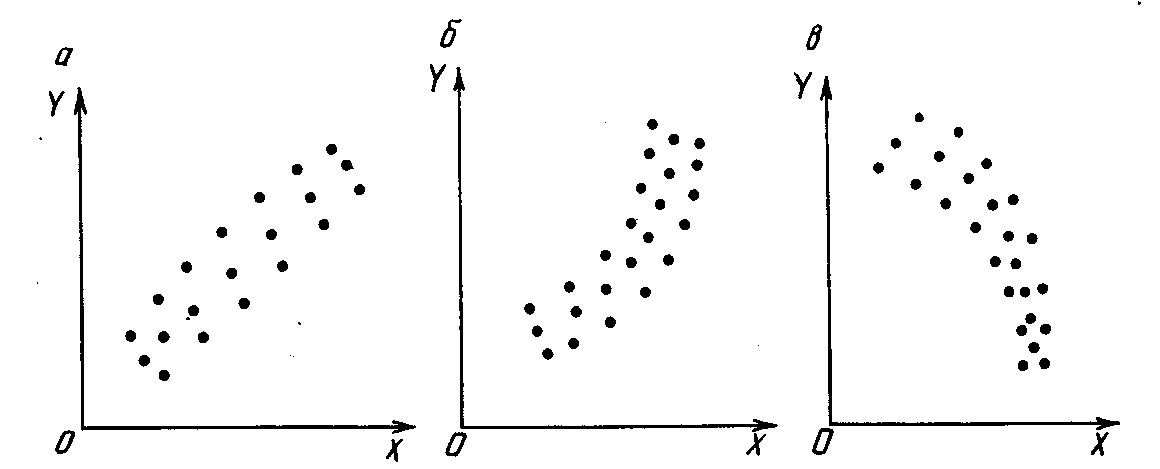Тема: Регрессионный анализ

1. Понятие многомерной выборки.

Во время статистических наблюдений для каждого объекта в ряде случаев можно измерить значения нескольких признаков. Таким образом, получается многомерная выборка. Если многомерную выборку обработать по значениям отдельного признака, то получится обычная обработка одномерной выборки.

Смысл обработки многомерных выборок состоит в том, чтобы установить связи между признаками.

Будем рассматривать двумерные выборки.

Две случайные величины могут быть связаны либо функциональной зависимостью (каждому значению одной величины соответствует определенное значение другой величины), либо зависимостью другого рода, называемой статистической, либо быть независимыми.

Статистической (стохастической) называют зависимость, при которой изменение одной величины вызывает изменение распределения другой величины.

В частности, статистическая зависимость проявляется в том, что одна из величин зависит не только от данной второй, но и от ряда случайных факторов, или когда среди условий, от которых зависят и та и другая величины, имеются общие для них обеих условия; в этом случае статистическую зависимость называют корреляционной. Зависимости такого рода можно описать, например, при помощи корреляционной таблицы.

2. Регрессия.

Регрессия (от лат. regressio – обратное движение) – зависимость среднего значения какой-либо величины от некоторой другой величины или от нескольких величин. При регрессионной связи одному и тому же значению могут соответствовать в зависимости от случая различные значения величины . Если при каждом значении наблюдается значений величины , то зависимость средних арифметических

от является регрессией в статистическом понимании этого термина. Примером такого рода зависимостей служит, в частности, зависимость средних диаметров сосен от их высот.

Изучение регрессии основано на том, что с.в. и с заданным совместным распределением вероятностей связаны вероятностной зависимостью: при каждом фиксированном значении величина является случайной величиной с определённым (зависящим от значения x) условным распределением вероятностей. Регрессия величины на определяется условным математическим ожиданием , вычисленным при условии, что :

. (2.1)

Аналогично определяется регрессия на

. (2.2)

Функции (2.1) и (2.2) называются функциями регрессии или модельными функциями регрессии соответственно на и на .

Уравнения

; (2.3)

называются уравнениями регрессии соответственно на и на . Линии, определяемые уравнениями (2.3), называются модельными линиями регрессии. Они вводятся только для непрерывных с.в.

Точность, с которой уравнение регрессии на отражает изменение в среднем при изменении , измеряется условной дисперсией величины , вычисленной для каждого значения :

. (2.4)

Линии регрессии обладают следующим свойством: среди всех действительных функций минимум математического ожидания достигается для функции , т.е. регрессия на дает наилучшее, в указанном смысле, представление величины по величине . Это свойство используется для прогноза по : если непосредственно наблюдается лишь компонента вектора , то в качестве прогнозируемого значения используют величину .

Если при всех значениях , то можно с достоверностью утверждать, что и связаны строгой функциональной зависимостью. Если ни при каком значении и не зависит от , то говорят, что регрессия на отсутствует. Аналогичным образом определяется регрессия на .

Задача регрессионного анализа состоит в том, чтобы по результатам наблюдений:

1) установить форму зависимости. Как правило, эта форма становится известной по опытным данным (рис. 2.1), где точками отмечены значения выборок (измерений);

2) определить функции регрессии. Процесс нахождения функции регрессии называется выравниванием отдельных значений зависимой переменной;

3) построить статистические оценки неизвестных параметров, входящих в уравнение регрессии;

4) проверить статистические гипотезы о регрессии;

5) проверить адекватность модели результатам наблюдений.

Рис. 2.1