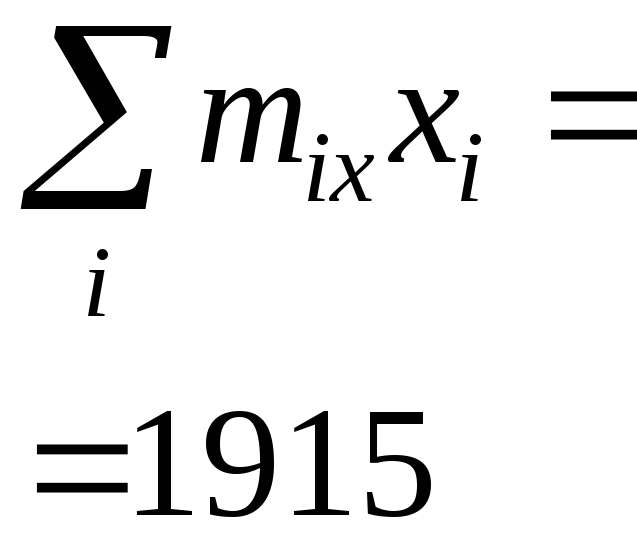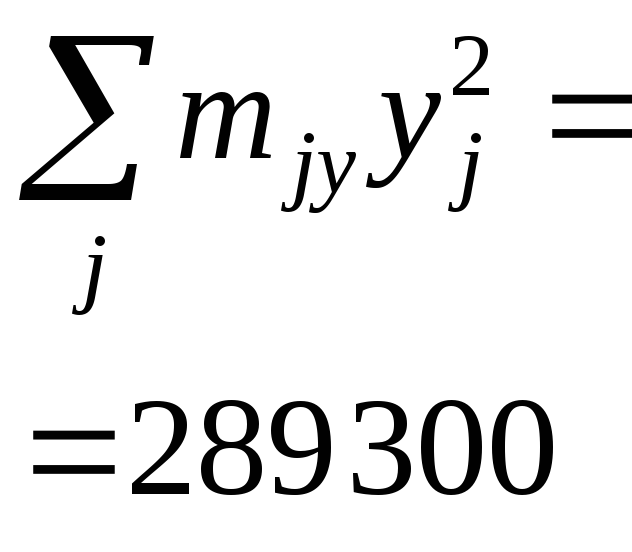3. Линейная регрессия.

Будем искать функцию регрессии в самом простом – линейном виде

, (3.1)

называемую регрессионной прямой или прямой регрессии.

Для определения этой функции, т.е. коэффициентов , используется метод наименьших квадратов (МНК).

Пусть – наблюдаемые (точные) значения, а – приближённое значение , вычисленное из уравнения регрессии. Тогда величина есть отклонение приближённого значения от точного (рис. 3.1).

Рис. 3.1

По методу наименьших квадратов неизвестные параметры и прямой регрессии определяют исходя из требования, состоящего в том, чтобы сумма квадратов отклонений была минимальной, т.е. из условия минимизации функции:

. (3.2)

Для нахождения минимума функции (3.2) запишем частные производные:

; .

Приравняв частные производные и нулю (необходимые условия минимума функции (3.2)), получим систему линейных уравнений для определения коэффициентов и :

(3.3)

Решив её, например, по формулам Крамера, найдём:

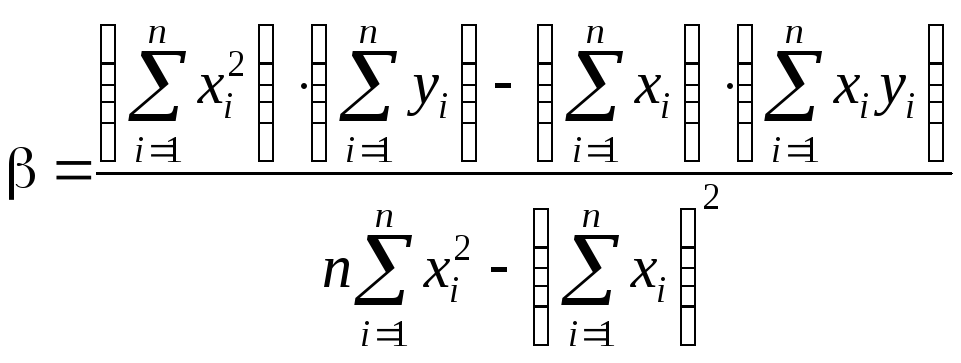; . (3.4)

Значения и , определённые по формулам (3.4), действительно доставляют минимум функции .

Прямая , для которой сумма квадратов достигает наименьшего значения, называется прямой выборочной регрессии.

Если требуется по экспериментальным данным получить линейное уравнение регрессии на , то в уравнении регрессии надо поменять местами переменные и . При этом получим уравнение , где и вычисляются по формулам:

; .(3.5)

Замечание. Регрессионные прямые и различны. Первая прямая получается в результате решения задачи о минимизации суммы квадратов отклонений по вертикали, а вторая – при решении задачи о минимизации суммы квадратов отклонений по горизонтали.

Пример 3.1. По данным таблицы наблюдений

	2	4	6
	5	3	7

составить уравнение регрессии на и на .

Δ Составим таблицу:

2	5	4	25	10
4	3	16	9	12
6	7	36	49	42

По формулам (3.4) при получаем:

; .

Следовательно, уравнение регрессии на есть

.

Аналогично по формулам (3.5) находим:

; .

Отсюда уравнение регрессии на есть

.

Нетрудно видеть, что регрессионные прямые и действительно различны. ▲

4. Построение регрессионной прямой по сгруппированным данным.

Если число измерений велико, то с целью упрощения расчётов экспериментальные данные нужно группировать, т.е. объединять в таблицу, называемую корреляционной:

Здесь – наблюдаемые значения, ; ; – частота появления пары ; – частота появления ; – частота появления ; – число всех наблюдений. Отсюда с учётом частот появлений переменных и

; ;

; ; .

Подставив эти суммы в формулы (3.4), получим:

;

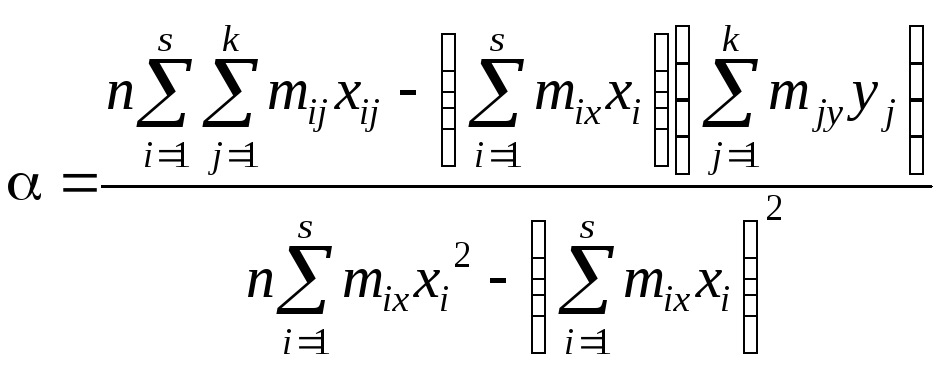. (4.1)

Пример 4.1. Найти уравнение прямой регрессии на по данным корреляционной таблицы:

	30	40	50	60	70
5	2	–	–	–	–	2
10	6	5	–	–	–	11
15	–	3	7	4	–	14
20	–	–	40	9	4	53
25	–	–	2	6	7	15
30	–	–	–	–	5	5
	8	8	49	19	16

Δ Для удобства вычислений построим вспомогательную таблицу.

	30	40	50	60	70
5	2	–	–	–	–	2	10	50
10	6	5	–	–	–	11	110	1100
15	–	3	7	4	–	14	210	3150
20	–	–	40	9	4	53	1060	21200
25	–	–	2	6	7	15	375	9375
30	–	–	–	–	5	5	150	4500
	8	8	49	19	16
	240	320	2450	1140	1120		–	–
	7200	12800	122500	68400	78400		–	–

Для нахождения двойной суммы нужно просуммировать произведения пар чисел на частоту их совместного появления:

.

По формулам (4.1) находим:

;

.

Таким образом, искомое уравнение регрессии есть

. ▲