5. Вероятность попадания нормально распределённой случайной величины в заданный интервал.

Выведем формулу для вероятности попадания с.в., распределённой по нормальному закону , в данный интервал . Поскольку плотность распределения вероятностей нормально распределённой с.в. есть

,

а вероятность попадания с.в. в интервал равна , то искомая вероятность

.

Введя замены , , , получим

,

где – функция Лапласа (6.2) (Тема: Последовательность независимых испытаний).

В частности, если интервал симметричен относительно м.о. , т.е. , , то последняя формула в силу нечётности функции приводится к виду

.

Пример 5.1. Положив в последней формуле и пользуясь таблицей значений функции , получаем

. ▲

Таким образом, с вероятностью 99,7 % значение нормально распределённой с.в. отклоняется от м.о. не больше, чем на . Другими словами, в среднем в трёх опытах из 1000 отклонение с.в. от м.о. будет более . Поэтому областью практически возможных значений нормально распределённых с.в. считается обычно интервал . В этом и состоит «правило трёх сигм».

6. Доверительный интервал для математического ожидания нормально распределённой генеральной совокупности при известной дисперсии.

Пусть независимые с.в. распределены по нормальному закону , причём дисперсия известна. Найдём доверительный интервал для математического ожидания .

Известно, что наилучшей оценкой м.о. является выборочное среднее , имеющее, согласно следствию из теоремы 5.2 (Тема: Первичная обработка выборок), нормальное распределение . Рассмотрим случайную величину

. (6.1)

Так как, , и , то с.в. (6.1) имеет нормальное распределение . Тогда для любого по интегральной теореме Муавра – Лапласа вероятность

,

где – функция Лапласа. Отсюда с учётом равенства (6.1) получим . Пусть эта вероятность равна , . Решив уравнение , найдём значение , при котором выполняется равенство

. (6.2)

Это равенство определяет вероятность того, что с доверительной вероятностью среднее значение отклоняется от м.о. генеральной совокупности на величину . Таким образом, с доверительной вероятностью можно утверждать, что интервал

(6.3)

является доверительным для оценки м.о.

В табл. 6.1 приводятся доверительные интервалы для м.о. нормально распределённых с.в. с известной дисперсией ( – объём выборки).

Таблица 6.1

Доверительный интервал	Надёжность	Вероятность ошибки
	0,9 (90 %)	0,1 (10 %)
	0,95 (95 %)	0,05 (5 %)
	0,99 (99 %)	0,01 (1 %)

Пример 6.1. Найти доверительный интервал для оценки м.о. с надёжностью 0,95, если , , .

Δ Из табл. 6.1 и формулы (6.3) получаем интервал

. ▲

При отыскании доверительных интервалов большую роль в статистике играют распределения хи-квадрат и -распределение Стьюдента².

7. Распределение хи-квадрат.

Пусть – независимые нормально распределённые по закону случайные величины и . Закон распределения с.в. называется хи-квадрат распределением с степенями свободы или -распределением Пирсона. Случайная величина с -распределением принимает только неотрицательные значения.

Можно убедиться, что с.в. имеет плотность вероятности

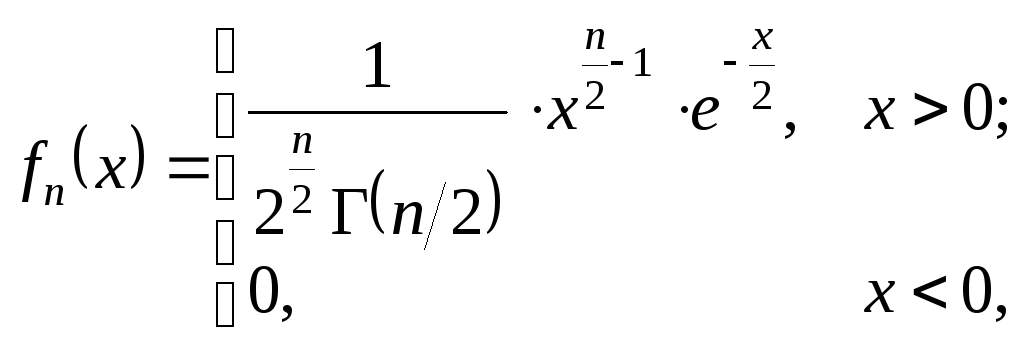(7.1)

где – гамма функция.

Найдём м.о. и дисперсию распределения . Для этого вычислим начальные моменты порядка . Имеем

.

Отсюда при получим соответственно:

;

так как , .

.

Тогда дисперсия .

Итак, для хи-квадрат распределения

; . (6.2)

Определим понятие -квантили случайной величины . Квантилью, отвечающей вероятности , или -квантилью (100-я процентиль) называется значение с.в. , при котором

, (7.3)

где – функция распределения с.в. . Ясно, что -квантиль есть медиана . Квантили и называются симметричными. Если распределение симметрично относительно нуля, то . Применение квантилей основывается, согласно формуле (3.7) (Тема: Скалярные случайные величины), на равенстве

. (7.4)

Для -распределения с степенями свободы -квантиль обозначается , где – объём выборки. Например, квантиль означает выполнение равенства , а квантиль – равенства . Квантили распределения приведены в таблице 4 в зависимости от числа степеней свободы и заданной доверительной вероятности .

Рис. 7.1

Замечание. Плотность распределения хи-квадрат как функция параметра обладает при малых длинным «правым хвостом», а при больших становится почти симметричной (рис. 7.1). Эти кривые называются кривыми Пирсона.