- •Тема: Скалярные случайные величины
- •Понятие случайной величины.
- •Закон распределения вероятностей случайной величины.
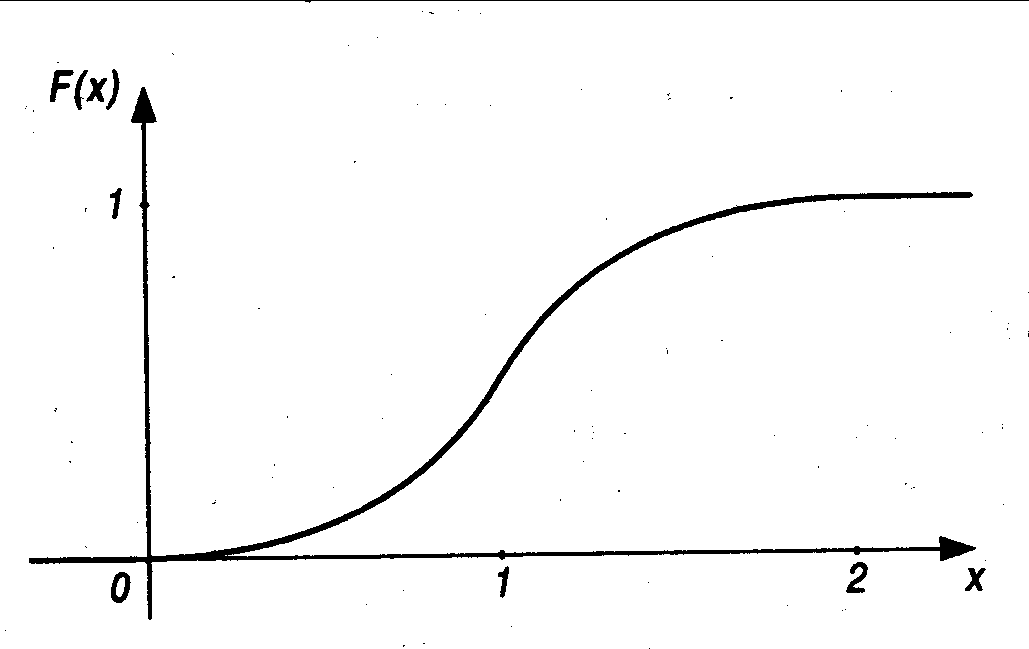
- •Функция распределения случайной величины.
- •Построение функции распределения дискретной случайной величины.
- •Плотность вероятности случайной величины.
- •Законы распределения некоторых случайных величин.
- •Функции от дискретных случайных величин.
- •Функции от непрерывных случайных величин.
-
Плотность вероятности случайной величины.
Плотностью
вероятности
с.в.
![]() или дифференциальной
функцией распределения
называется предел
или дифференциальной
функцией распределения
называется предел
![]() ,
(5.1)
,
(5.1)
если он существует.
Пусть
![]() – функция распределения с.в.
– функция распределения с.в.
![]() .
Если существует
.
Если существует
![]() ,
то равенство (5.1) равносильно соотношению
,
то равенство (5.1) равносильно соотношению
![]() .
(5.2)
.
(5.2)
Итак, плотность вероятности равна производной от функции распределения.
Выясним свойства плотности вероятности.
10.
Функция
![]() ,
,
![]() .
.
20. Справедливо равенство
![]() .
(5.3)
.
(5.3)
30.
Если
![]() – плотность вероятности с.в.
– плотность вероятности с.в.
![]() ,
то
,
то
![]() .
(5.4)
.
(5.4)
40. Имеет место соотношение
![]() ,
(5.5)
,
(5.5)
называемое условием нормировки.
Пример
5.1.
Плотность
вероятности с.в.
![]() есть
есть
![]() ,
,
![]() ,
,
![]() .
Найти: а) коэффициент
.
Найти: а) коэффициент
![]() ;
б) функцию распределения
;
б) функцию распределения
![]() ;
в) вероятность попадания с.в. в интервал
;
в) вероятность попадания с.в. в интервал
![]() .
.
D а) Из условия нормировки (5.5) имеем
![]() .
.
Следовательно,
![]() .
.
б) По формуле (5.4)
![]() .
.
в) Согласно равенству (3.7),
![]() .
▲
.
▲
Пример
5.2.
Найти
функцию распределения
![]() с.в.
с.в.
![]() ,
плотность
вероятности которой определена функцией
,
плотность
вероятности которой определена функцией
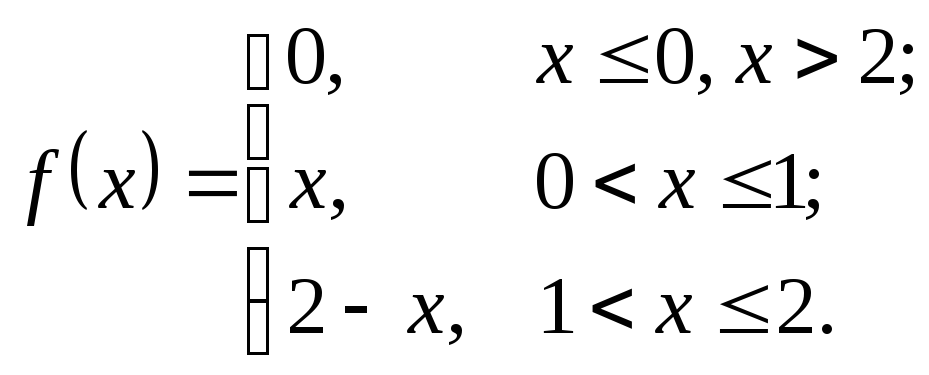
D
Чтобы найти функцию распределения
![]() ,
воспользуемся формулой (5.4).
,
воспользуемся формулой (5.4).
При
![]() получаем
получаем
![]() .
.
При
![]() находим
находим
![]() .
.
Когда
![]() ,
то
,
то
![]()
![]() .
.
При
![]() получаем
получаем
![]() .
.
Таким образом, искомая функция распределения имеет вид
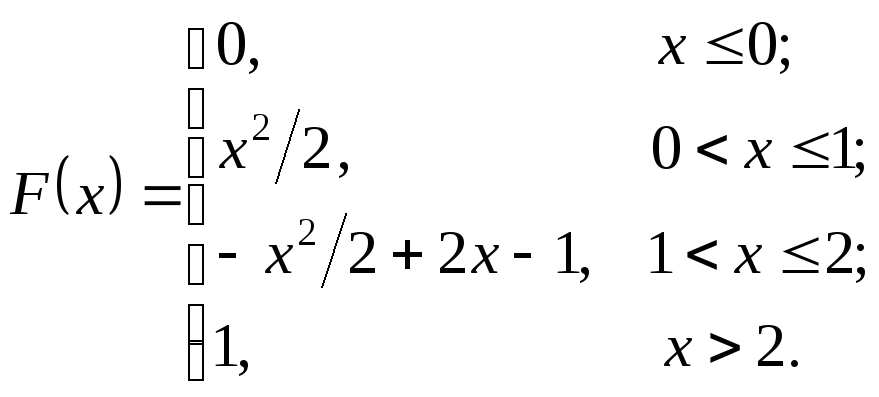
|
Рис. 5.2 |
Рис. 5.3 |
Графики функций
![]() и
и
![]() изображены на рис. 5.2 и 5.3 соответственно.
▲
изображены на рис. 5.2 и 5.3 соответственно.
▲
-
Законы распределения некоторых случайных величин.
Приведём несколько наиболее употребительных законов распределения с.в.
1) Биномиальный
закон. В
схеме испытаний Бернулли функция
распределения
![]() имеет вид ступенчатой функции с разрывами
в точках
имеет вид ступенчатой функции с разрывами
в точках
![]() ,
причём величина скачка в точке
,
причём величина скачка в точке
![]() равна
равна
![]() (см. пример 2.2).
(см. пример 2.2).
2) Распределение
Пуассона.
С.в.
![]() называется распределённой по
закону Пуассона,
если она принимает дискретные значения
из ряда чисел
называется распределённой по
закону Пуассона,
если она принимает дискретные значения
из ряда чисел
![]() с вероятностями
с вероятностями
![]() ,
,
где
![]() – параметр распределения.
– параметр распределения.
Покажем, что
![]() .
Действительно,
.
Действительно,
![]() .
.
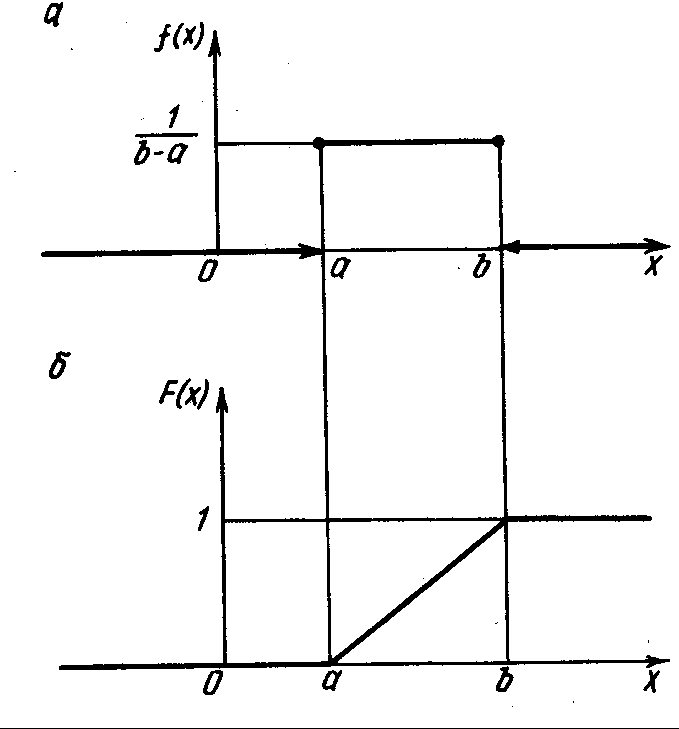
3) Равномерное
распределение.
С.в.
![]() называется равномерно
распределённой
на отрезке
называется равномерно
распределённой
на отрезке
![]() ,
если её плотность вероятности
,
если её плотность вероятности
 (6.1)
(6.1)
Функция распределения
равномерно распределённой с.в. получена
в примере 4.2. Графики функций
![]() и
и
![]() изображены на рис. 6.1, а
и б
соответственно.
изображены на рис. 6.1, а
и б
соответственно.
|
Рис. 6.1 |
Рис.6.2 |
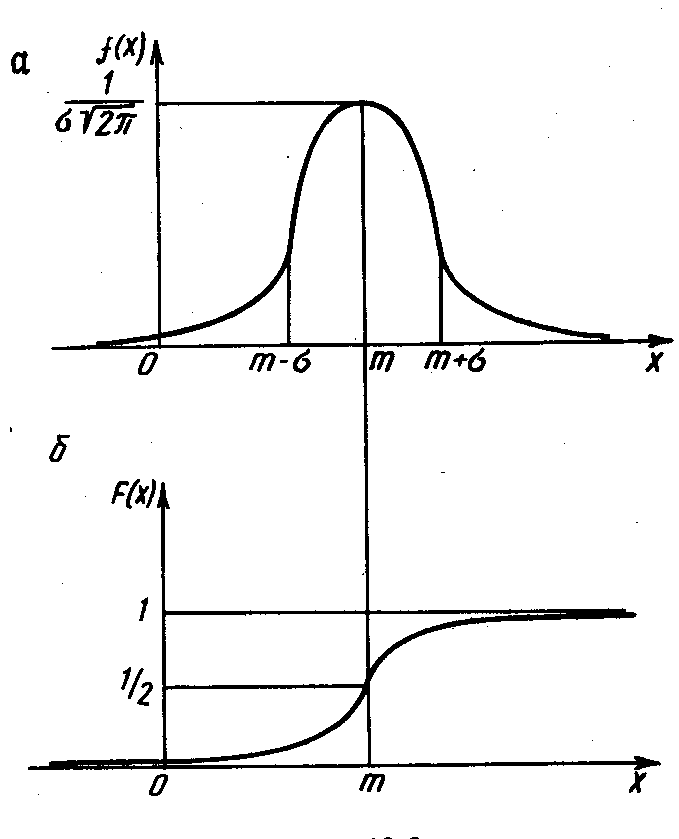
4) Нормальное
распределение
(распределение Гаусса). С.в.
![]() называется распределённой по
нормальному закону
или имеет гауссовское
распределение,
если её плотность вероятности имеет
вид
называется распределённой по
нормальному закону
или имеет гауссовское
распределение,
если её плотность вероятности имеет
вид
 ,
,
![]() .
(6.2)
.
(6.2)
Согласно формуле (5.4), её функция распределения
 .
(6.3)
.
(6.3)
Как видно из формул
(6.2) и (6.3), нормальное распределение
зависит от параметров
![]() и
и
![]() и полностью определяется ими. Графики
функций
и полностью определяется ими. Графики
функций
![]() и
и
![]() изображены на рис. 6.2, а
и б
соответственно. Максимум ординаты
кривой
изображены на рис. 6.2, а
и б
соответственно. Максимум ординаты
кривой
![]() равен
равен
![]() .
Отсюда следует, что чем больше
.
Отсюда следует, что чем больше
![]() ,
тем шире кривая и тем ниже её максимум.
График плотности
,
тем шире кривая и тем ниже её максимум.
График плотности
![]() симметричен относительно прямой
симметричен относительно прямой
![]() .
В сокращённом виде нормальное распределение
записывается так:
.
В сокращённом виде нормальное распределение
записывается так:
![]() или
или
![]() .
При
.
При
![]() ,
,
![]() получаем так называемое стандартное
(нормированное)
нормальное
распределение
получаем так называемое стандартное
(нормированное)
нормальное
распределение
![]()
![]() .
(6.4)
.
(6.4)
Для функции (6.4)
имеет место соотношение
![]() .
Для значений
.
Для значений
![]() при
при
![]()
![]() составлены таблицы, которые можно найти
в рекомендуемой литературе.
составлены таблицы, которые можно найти
в рекомендуемой литературе.
5) Экспоненциальное
распределение.
С.в.
![]() называется распределённой по
экспоненциальному закону,
если плотность распределения вероятностей
называется распределённой по
экспоненциальному закону,
если плотность распределения вероятностей
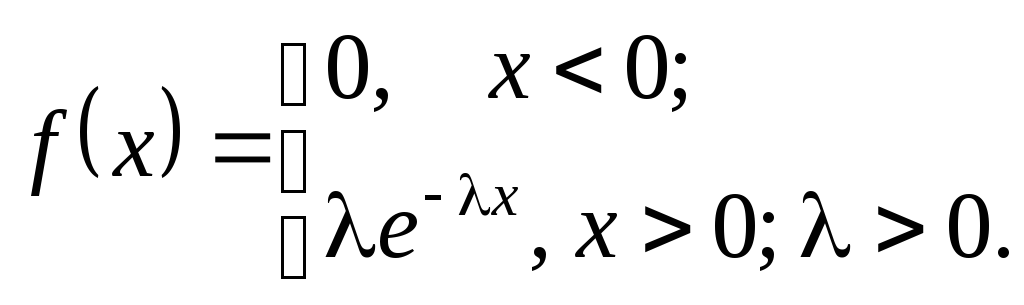 (6.4)
(6.4)
Отсюда функция распределения
 (6.5)
(6.5)
Пример
6.1.
Найти
функцию распределения
![]() случайной
величины
случайной
величины
![]() ,
распределённой
по нормальному закону, через функцию
Лапласа.
,
распределённой
по нормальному закону, через функцию
Лапласа.
D В соответствии с формулой (6.3)
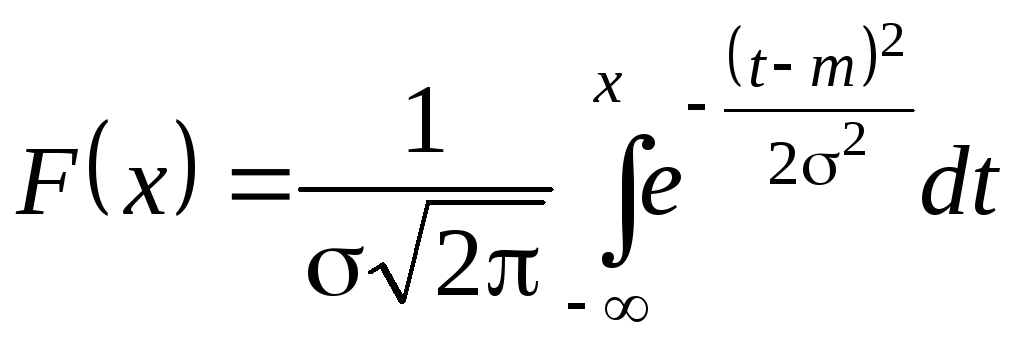 .
.
Переходим к новой
переменной
![]() ,
тогда
,
тогда
![]() ,
,
![]() .
Поэтому
.
Поэтому

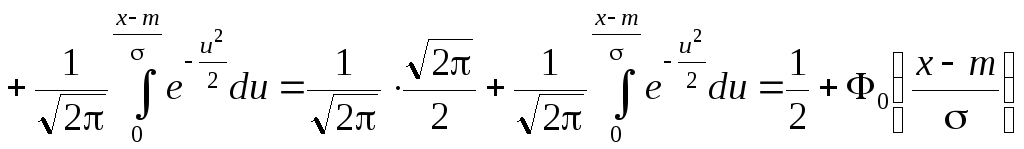 ,
,
![]() ,
(6.6)
,
(6.6)
где
![]() – функция Лапласа, определяемая формулой
(6.2) (Тема: Последовательность независимых
испытаний).
– функция Лапласа, определяемая формулой
(6.2) (Тема: Последовательность независимых
испытаний).
Здесь принято во внимание, что
![]() .
.
Это равенство следует из цепочки равенств:
![]() (интеграл Пуассона)
(интеграл Пуассона)
![]()
![]()
![]()
![]()
![]() ,
,
так как
![]() – чётная функция.
– чётная функция.
Согласно равенствам
(3.7) и (6.6), вероятность попадания значений
нормально распределённой случайной
величины
![]() в интервал
в интервал
![]() определяется формулой
определяется формулой
![]() .
▲ (6.7)
.
▲ (6.7)