3. Функция распределения случайной величины.

Пусть – вероятностное пространство и – с.в. Тогда , , является событием и, следовательно, для каждого определена вероятность

. (3.1)

Функция (3.1), определённая для всех , называется функцией распределения с.в. или интегральной функцией распределения с.в. .

Выясним её свойства.

1⁰. Значения принадлежат отрезку , т.е. , . Это следует из того, что есть вероятность события .

2⁰. – неубывающая функция, т.е. .

3⁰. Если с.в. принимает возможное значение с вероятностью , то её функция распределения имеет в точке разрыв первого рода со скачком . В точке функция непрерывна слева, т.е. .

Замечание. Свойство 3⁰ функции является следствием её определения (3.1) как вероятности . Если же определить соотношением , то можно доказать, что непрерывна справа в каждой точке .

4⁰. Справедливы равенства , .

5⁰. Вероятность того, что с.в. принимает значения из промежутка ,

. (3.5)

6⁰. Имеет место равенство

. (3.6)

7⁰. Справедливы формулы: а) ;

б) ; в) .

Случайная величина называется непрерывной, если её функция распределения непрерывна.

8⁰. Если – непрерывная с.в., то вероятность того, что она принимает любое конкретное значение , равна нулю, т.е. .

9⁰. Если – непрерывная с.в., то

. (3.7)

Соотношение (3.7) следует из свойств 5⁰ и 7⁰ и непрерывности функции .

10⁰. Если возможные значения с.в. принадлежат отрезку , то

(3.8)

Длина отрезка называется размахом с.в. .

Формула (3.8) следует из определения функции .

Итак, всякое вероятностное пространство с.в. определяет по формуле (3.1) однозначную действительную неотрицательную функцию , , обладающую свойствами 1⁰ – 10⁰. Основными из них, полностью характеризующими , являются приведённые ниже свойства:

1⁰. , .

2⁰. .

3⁰. , т.е. непрерывна в точке слева.

4⁰. , .

Можно показать, что всякая функция, обладающая свойствами 1⁰ – 4⁰, задаёт распределение вероятностей на подмножествах , . Для этого достаточно каждому такому интервалу поставить в соответствие вероятность .

Пример 3.1. Установить, какая из функций

а) б)

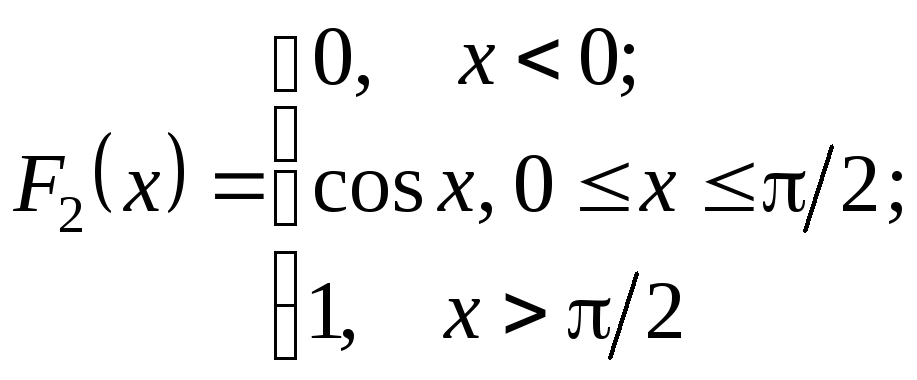
является функцией распределения некоторой непрерывной с.в. В случае утвердительного ответа найти вероятность того, что соответствующая с.в. принимает значения между –1 и 2.

Рис. 3.2

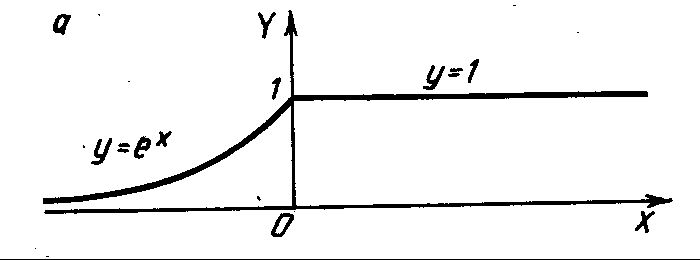
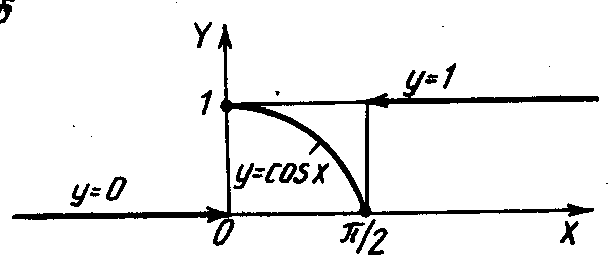
D Графики функций и изображены на рис. 3.2, а и б соответственно. Из них видно, что только функция является функцией распределения некоторой с.в. Для неё по формуле (3.7) вероятность . ▲

4. Построение функции распределения дискретной случайной величины.

Распределение дискретной с.в. задаётся таблицей (2.1). Используя свойства функции , получаем, что при

.

В точке , согласно свойству 3⁰, имеет скачок и, значит, для

.

Таким образом, функция распределения дискретной с.в. кусочно-постоянна, имеет скачки в точках разрыва и непрерывна слева в точках разрыва . График функции изображён на рис. 4.1.

Рис. 4.1

Пример 4.1. С.в. принимает значения , , с вероятностями . Найти функцию распределения и вероятность события .

D Пусть , . Событие означает, что с.в. принимает значения с вероятностями соответственно. Тогда функция распределения

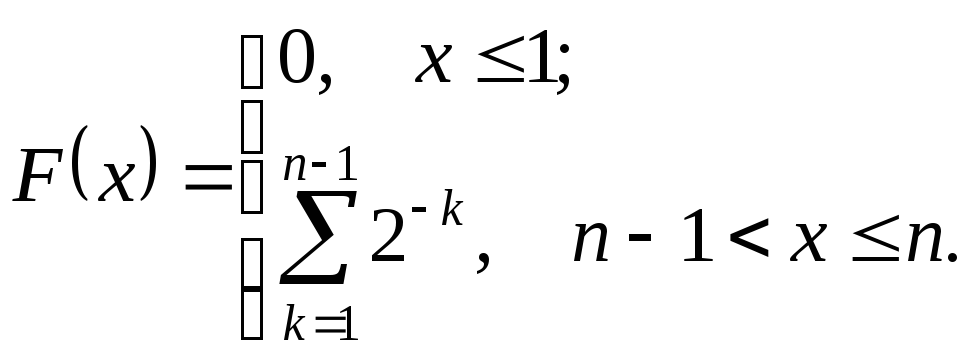
Событию отвечают значения 3, 4, 5, 6 с вероятностями , , , соответственно. Тогда

. ▲

Пример 4.2. На отрезке случайным образом появляется точка. Найти функцию распределения с.в. – координаты появившейся точки.

Рис. 4.2

D Событие означает, что появившаяся точка находится на интервале . При событие невозможно. Тогда . При вероятность появления точки на есть , так как – длина отрезка , а – длина всего отрезка (рис. 4.2). При событие достоверно, т.е. . Таким образом, искомая функция распределения имеет вид

▲