Транспортная задача (тз)

Пусть задано n пунктов (складов), в которых накоплено сырье какого-то вида. Количество сырья в i-м складе обозначим а_i . Существует m-пунктов (потребителей), в которые надо завести это сырье. Количество сырья, которое надо завести к j-у потребителю обозначим b_j .

Сначала будем считать, что количество имеющегося на складах сырья и количество требуемого для потребителей сырья совпадают, то есть выполняется условие баланса имеют вид:

Введем матрицу стоимости С, элемент которой c_ij представляет собой стоимость перевозки единицы сырья из i-го склада к j -у потребителю.

Введем также матрицу плана перевозок Х, элемент которой есть искомое плановое количество ресурса, которое следует перевезти изi-го склада к j -у потребителю.

На элементы матрицы плана Х накладываются следующие ограничения:

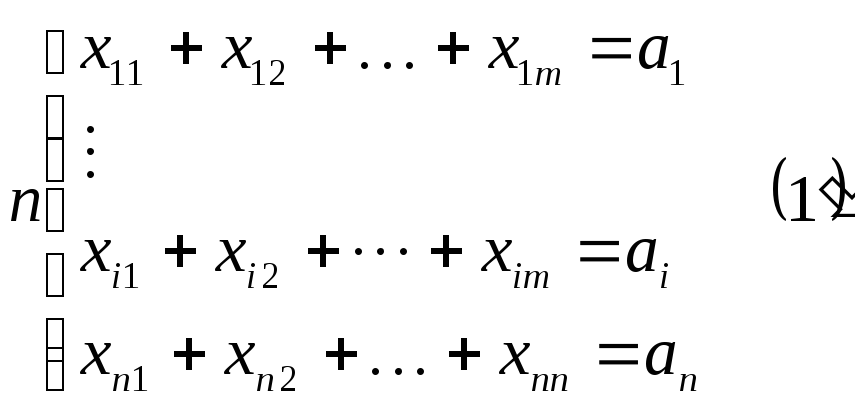
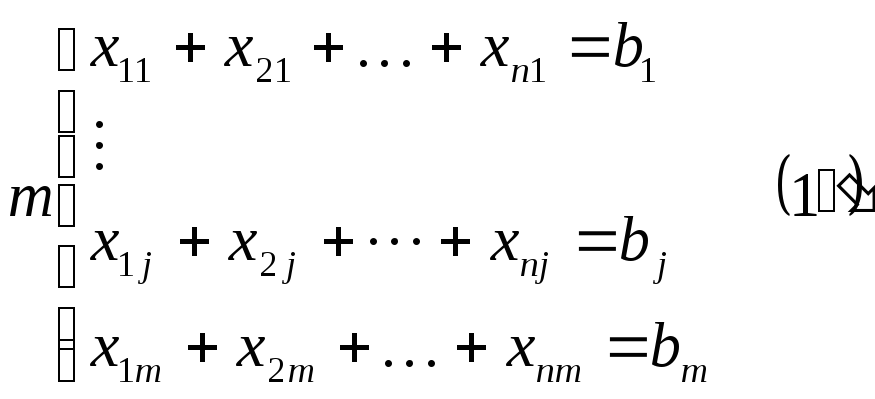
Целевая функция транспортной задачи имеет вид:

(2)

Имеются также естественные ограничения

Xij 0 (3)

Задача формулируется следующим образом: необходимо найти такую матрицу , для которой выполняются условия (1^/, 1^//, 3) и целевая функция принимает минимальное значение:

(4)

Эта задача является частным случаем ОЗЛП. Главная особенность в том, что коэффициенты системы уравнений (1^/, 1^//) принимают только два значения – 1 и 0. По этой причине СМ применительно к ТЗ может быть упрощен. В данном случае он принимает вид либо распределительного метода, либо метода потенциалов.

Другой особенностью ТЗ является то, что, как мы увидим, исходное базисное решение ищется значительно проще, чем в ОЗЛП.

Третья особенность, состоящая в том, что план ищется в виде матрицы, а не в виде вектора, несущественна.

Для работы по СМ необходимо знать ранг матрицы ограничений.

Поэтому начнем решение задачи с определения ранга системы ограничений (1^/, 1^//)

Теорема о ранге матрицы ограничений ТЗ.

Ранг системы ограничений (1^/, 1^//) r равен n + m -1.

Доказательство основано на том, что из n уравнений (1^/) легко выражаются n переменных вида x_j₁, то есть те, у которых второй индекс равен 1. Так же из второй системы (1^//) выразим все переменные вида x₁_j, у которых первый индекс равен 1. Всего получим n+m формул, выражающих одни переменные через другие. Но две из них выражают одну и ту же переменную, а именно х₁₁. Всего получим n + m -1 различных формул. Это доказывает, что ранг матрицы Удовлетворяет неравенству r n + m -1.

С другой стороны всего в системах (1^/, 1^//) имеется n+m уравнений, причем между ними имеется одна линейная зависимость. Действительно, если сложить отдельно все уравнения (1^/) и все уравнения (1^//) то в силу уравнения баланса получим одно и то же число, то есть

Это значит, что r n + m -1.

Вывод: ранг системы равен n + m -1.

Циклы в матрицах и их свойства

Цикл в матрице – это замкнутая ломаная, каждое звено которой лежит либо в одной строке, либо в одном столбце. Эти звенья начинаются и заканчиваются в ячейках матрицы, которые называются вершинами звена.

В каждой вершине могут встречаются только два звена, причем они должны образовывать между собой прямой угол. Это значит, что двигаясь вдоль цикла и придя в некоторую вершину по строке, мы должны уходить по столбцу, а придя в вершину по столбцу, должны уходить по строке.