
- •Транспортная задача (тз)
- •Xij 0 (3)
- •Циклы в матрицах и их свойства
- •Теорема о существовании цикла
- •Доказательство теоремы о существовании цикла
- •Распределительный метод решения тз
- •Теорема о сдвиге по циклу.
- •Определение.
- •Переходим к изложению распределительного метода Алгоритм работы по распределительному методу
- •Решение транспортной задачи методом потенциалов
- •Теорема
- •Решение несбалансированных задач тзлп
Переходим к изложению распределительного метода Алгоритм работы по распределительному методу
Находится некоторое базисное решение методом северо-западного угла или наименьшей стоимости, которое заносится в матрицу плана перевозок.
При этом все клетки матрицы считаются необсчитанными («незачеркнутыми»)
Для любой еще необсчитанной (незачеркнутой) свободной клетки строится ее цикл пересчета. Если таких клеток нет, то следует перейти к п. 5.
Осуществляется алгебраическое суммирование по построенному циклу пересчета выбранной в пункте 2 свободной клетки.
Если результат, полученный в п. 2 является неотрицательным числом, то зачеркнуть эту клетку, т.е. считать ее обсчитанной, и перейти к п. 1, иначе перейти к следующему пункту.
Найти в цикле пересчета такую отрицательную вершину, значение плана перевозок которой М минимально среди отрицательных вершин. Назовем ее «минимальной». Осуществить сдвиг по циклу пересчета на эту величину. При этом мы перейдем к новому базисному решению, в котором:
а) Свободной стала та базисная клетка, которая была выбрана как минимальная и ее новое значение равно 0.
б) Новой базисной переменной стала старая свободная, которая приобрела минимальное значение М.
в) Все базисные переменные положительных вершин увеличились, а все отрицательные уменьшились на величину М. При этом ни одна из них не стала меньше 0, т.е. полученное решение осталось допустимым. Уберем зачеркивание всюду, где оно было поставлено и перейдем к п. 1.
Целевая функция уменьшилась на величину стоимости, записанной в матрице стоимостей С в ячейке, соответствующей минимальной базисной переменной.
Переход к пункту 1.
Успешный конец алгоритма, т.к. последнее решение оптимально.
Решение транспортной задачи методом потенциалов
Самым трудоемким этапом распределительного метода является тот, на котором мы ищем ту свободную переменную, для которой алгебраическое суммирование по циклу пересчета дает в результате отрицательное число (см. пункты 2 и 3 алгоритма).
Метод потенциалов заменяет эти пункты более экономной процедурой.
Напомним, для чего производится алгебраическое суммирование по циклу пересчета
В симплекс-методе
производится переход от одного базисного
решения к другому с улучшением значения
целевой функции. Для этого среди свободных
переменных ищется такая, для которой
коэффициент ![]() в
разложении целевой функции по свободным
переменным
в
разложении целевой функции по свободным
переменным
![]()
отрицателен. Это позволяет за счет увеличения этой свободной переменной от нуля до некоторого положительного значения уменьшить целевую функцию и, следовательно, улучшить план перевозок.
Процедура
алгебраического суммирования по циклу
пересчета свободной переменной как раз
производит расчет коэффициента ![]() для
соответствующей переменной.
для
соответствующей переменной.
Метод потенциалов
отличается от распределительного метода
способом расчета коэффициента ![]() ,
который менее трудоемок. Изложим этот
способ.
,
который менее трудоемок. Изложим этот
способ.
Пусть имеем
некоторое базисное решение. Свяжем с
к-й
строкой матрицы перевозок величину
![]() (к
= 1,…n)
, а с s-м
столбцом свяжем величину
(к
= 1,…n)
, а с s-м
столбцом свяжем величину
![]() (s
= 1,…m).
Назовем эти величины потенциалами. Их
общее число равно n+m.
(s
= 1,…m).
Назовем эти величины потенциалами. Их
общее число равно n+m.
Для каждой пары
потенциалов (![]() ,
,![]() )
составим уравнение
)
составим уравнение
![]() .
(*)
.
(*)
Здесь
![]() -
соответствующий элемент матрицы
стоимости, соответствующий некоторой
базисной ячейки. Очевидно, что число
таких уравнений равно
n+m-1.
Будем рассматривать эти уравнения как
систему из n+m
-1уравнений относительно n+m
неизвестных потенциалов.
-
соответствующий элемент матрицы
стоимости, соответствующий некоторой
базисной ячейки. Очевидно, что число
таких уравнений равно
n+m-1.
Будем рассматривать эти уравнения как
систему из n+m
-1уравнений относительно n+m
неизвестных потенциалов.
Оказывается, что ранг системы равен n+m-1. Это значит, что значение одного из потенциалов мы можем выбрать произвольно, а остальные определить из уравнений (*).
Пример.
Продемонстрируем цепной способ решения систем вида (*)
Рассмотрим подобную систему.
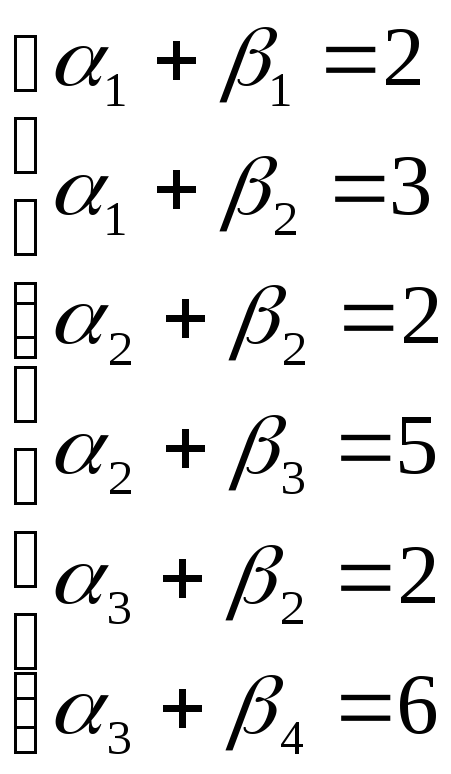
Здесь n=3, m=4.
Потенциал
![]() входит сразу в два уравнения. Произвольно
зададим именно его значение.
входит сразу в два уравнения. Произвольно
зададим именно его значение.
Пусть
![]() Тогда из первых двух уравнений получим
Тогда из первых двух уравнений получим
![]()
![]()
Тогда из третьего
уравнения
![]()
Далее из четвертого
уравнения , а из пятого
![]()
Наконец, из
последнего уравнения имеем
![]()
Найдя потенциалы,
мы можем определить все коэффициенты
![]() .
Справедлива следующая
.
Справедлива следующая
