

|
Потенциал |
|
|
электрического |
|
|
поля |
|
|
Примеры |
|
|
применения |
|
|
теоремы Гаусса |
|
|
|
|
|
Потенциал поля |
|
|
точечного заряда |
|
|
Работа силы |
|
|
Кулона |
|
|
Потенциальная |
|
|
энергия |
|
2. Потенциал поля точечного заряда |
Понятие |
|
потенциала |
||
|
||
|
Единица |
|
|
измерения |
|
|
потенциала |
|
|
Потенциал |
|
|
системы зарядов |
|
|
Связь |
|
|
напряжённости и |
|
|
потенциала |
|
|
Эквипотенциальны |
|
|
поверхности |
|
|
Циркуляции |
|
|
вектора |
|
|
|
12/32
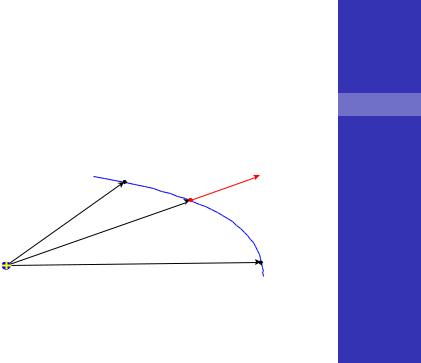
Работа силы Кулона
Найд¼м работу сил поля, созданного точечным зарядом, по перемещению пробного заряда ′ из точки 1 в
точку 2. Считаем и ′ одноим¼нными.
|
|
~ |
|
|
1 |
F |
|
~r1 |
q′ |
||
|
|||
|
|
||
|
|
~r |
|
|
|
2 |
|
|
|
~r2 |
Потенциал
электрического
поля
Примеры
применения теоремы Гаусса
Потенциал поля точечного заряда
Работа силы Кулона
Потенциальная
энергия
Понятие
потенциала
Единица
измерения
потенциала
Потенциал системы зарядов
Связь напряжённости и потенциала
Эквипотенциальны
поверхности
Циркуляции вектора
13/32
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
d|~r| |
|
F |
|
|
|||
|
|
|
|
|
|
|
|
q′ |
|
|
|
|
|
||||
|
|
|
|
|
|
|
~r1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d~r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
~r2 |
|
|
||
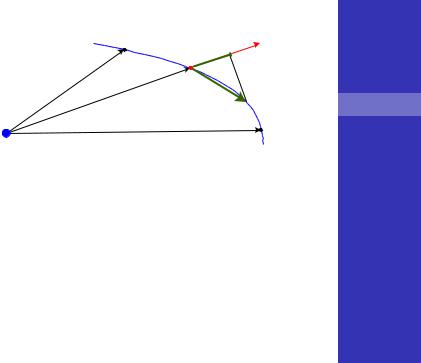
Работа на элементарном пути : |
|
|
|
|
|
|
|
|
|||||||||
|
|
1 |
|
′ |
|
1 |
|
′ |
| | = |
|
1 |
|
′ |
|
|||
= = |
4 0 |
|
3 |
= |
4 0 |
|
3 |
|
4 0 |
2 |
|
||||||
Работа силы Кулона зависит только от начальной и конечной точки и не зависит от формы траектории:
12 = ∫ |
2 |
|
2 |
2 |
= 4 0′ 1 |
− 4 0′ 2 |
||
= 4 ′0 |
∫ |
|||||||
|
|
|
|
|
|
|
|
|
11
Потенциал
электрического
поля
Примеры
применения теоремы Гаусса
Потенциал поля точечного заряда
Работа силы Кулона
Потенциальная
энергия
Понятие
потенциала
Единица
измерения
потенциала
Потенциал системы зарядов
Связь напряжённости и потенциала
Эквипотенциальны
поверхности
Циркуляции вектора
14/32

|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
d|~r| |
|
F |
|
|
|||
|
|
|
|
|
|
|
|
q′ |
|
|
|
|
|
||||
|
|
|
|
|
|
|
~r1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d~r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
~r2 |
|
|
||
Работа на элементарном пути : |
|
|
|
|
|
|
|
|
|||||||||
|
|
1 |
|
′ |
|
1 |
|
′ |
| | = |
|
1 |
|
′ |
|
|||
= = |
4 0 |
|
3 |
= |
4 0 |
|
3 |
|
4 0 |
2 |
|
||||||
Работа силы Кулона зависит только от начальной и конечной точки и не зависит от формы траектории:
12 = ∫ |
2 |
|
2 |
2 |
= 4 0′ 1 |
− 4 0′ 2 |
||
= 4 ′0 |
∫ |
|||||||
|
|
|
|
|
|
|
|
|
11
Потенциал
электрического
поля
Примеры
применения теоремы Гаусса
Потенциал поля точечного заряда
Работа силы Кулона
Потенциальная
энергия
Понятие
потенциала
Единица
измерения
потенциала
Потенциал системы зарядов
Связь напряжённости и потенциала
Эквипотенциальны
поверхности
Циркуляции вектора
14/32

|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
d|~r| |
|
F |
|
|
|||
|
|
|
|
|
|
|
|
q′ |
|
|
|
|
|
||||
|
|
|
|
|
|
|
~r1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d~r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
~r2 |
|
|
||
Работа на элементарном пути : |
|
|
|
|
|
|
|
|
|||||||||
|
|
1 |
|
′ |
|
1 |
|
′ |
| | = |
|
1 |
|
′ |
|
|||
= = |
4 0 |
|
3 |
= |
4 0 |
|
3 |
|
4 0 |
2 |
|
||||||
Работа силы Кулона зависит только от начальной и конечной точки и не зависит от формы траектории:
12 = ∫ |
2 |
|
2 |
2 |
= 4 0′ 1 |
− 4 0′ 2 |
||
= 4 ′0 |
∫ |
|||||||
|
|
|
|
|
|
|
|
|
11
Потенциал
электрического
поля
Примеры
применения теоремы Гаусса
Потенциал поля точечного заряда
Работа силы Кулона
Потенциальная
энергия
Понятие
потенциала
Единица
измерения
потенциала
Потенциал системы зарядов
Связь напряжённости и потенциала
Эквипотенциальны
поверхности
Циркуляции вектора
14/32
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
d|~r| |
|
F |
|
|
|||
|
|
|
|
|
|
|
|
q′ |
|
|
|
|
|
||||
|
|
|
|
|
|
|
~r1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d~r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
~r2 |
|
|
||
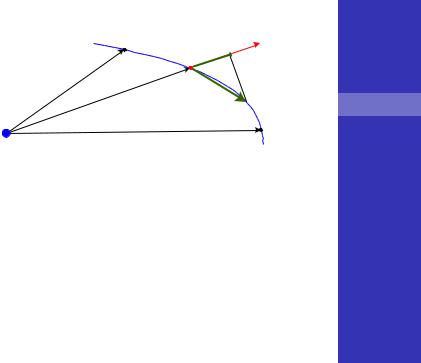
Работа на элементарном пути : |
|
|
|
|
|
|
|
|
|||||||||
|
|
1 |
|
′ |
|
1 |
|
′ |
| | = |
|
1 |
|
′ |
|
|||
= = |
4 0 |
|
3 |
= |
4 0 |
|
3 |
|
4 0 |
2 |
|
||||||
Работа силы Кулона зависит только от начальной и конечной точки и не зависит от формы траектории:
12 = ∫ |
2 |
|
2 |
2 |
= 4 0′ 1 |
− 4 0′ 2 |
||
= 4 ′0 |
∫ |
|||||||
|
|
|
|
|
|
|
|
|
11
Потенциал
электрического
поля
Примеры
применения теоремы Гаусса
Потенциал поля точечного заряда
Работа силы Кулона
Потенциальная
энергия
Понятие
потенциала
Единица
измерения
потенциала
Потенциал системы зарядов
Связь напряжённости и потенциала
Эквипотенциальны
поверхности
Циркуляции вектора
14/32

|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
d|~r| |
|
F |
|
|
|||
|
|
|
|
|
|
|
|
q′ |
|
|
|
|
|
||||
|
|
|
|
|
|
|
~r1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d~r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
~r2 |
|
|
||
Работа на элементарном пути : |
|
|
|
|
|
|
|
|
|||||||||
|
|
1 |
|
′ |
|
1 |
|
′ |
| | = |
|
1 |
|
′ |
|
|||
= = |
4 0 |
|
3 |
= |
4 0 |
|
3 |
|
4 0 |
2 |
|
||||||
Работа силы Кулона зависит только от начальной и конечной точки и не зависит от формы траектории:
12 = ∫ |
2 |
|
2 |
2 |
= 4 0′ 1 |
− 4 0′ 2 |
||
= 4 ′0 |
∫ |
|||||||
|
|
|
|
|
|
|
|
|
11
Потенциал
электрического
поля
Примеры
применения теоремы Гаусса
Потенциал поля точечного заряда
Работа силы Кулона
Потенциальная
энергия
Понятие
потенциала
Единица
измерения
потенциала
Потенциал системы зарядов
Связь напряжённости и потенциала
Эквипотенциальны
поверхности
Циркуляции вектора
14/32

|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
d|~r| |
|
F |
|
|
|||
|
|
|
|
|
|
|
|
q′ |
|
|
|
|
|
||||
|
|
|
|
|
|
|
~r1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d~r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
~r2 |
|
|
||
Работа на элементарном пути : |
|
|
|
|
|
|
|
|
|||||||||
|
|
1 |
|
′ |
|
1 |
|
′ |
| | = |
|
1 |
|
′ |
|
|||
= = |
4 0 |
|
3 |
= |
4 0 |
|
3 |
|
4 0 |
2 |
|
||||||
Работа силы Кулона зависит только от начальной и конечной точки и не зависит от формы траектории:
12 = ∫ |
2 |
|
2 |
2 |
= 4 0′ 1 |
− 4 0′ 2 |
||
= 4 ′0 |
∫ |
|||||||
|
|
|
|
|
|
|
|
|
11
Потенциал
электрического
поля
Примеры
применения теоремы Гаусса
Потенциал поля точечного заряда
Работа силы Кулона
Потенциальная
энергия
Понятие
потенциала
Единица
измерения
потенциала
Потенциал системы зарядов
Связь напряжённости и потенциала
Эквипотенциальны
поверхности
Циркуляции вектора
14/32
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
d|~r| |
|
F |
|
|
|||
|
|
|
|
|
|
|
|
q′ |
|
|
|
|
|
||||
|
|
|
|
|
|
|
~r1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d~r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
~r2 |
|
|
||
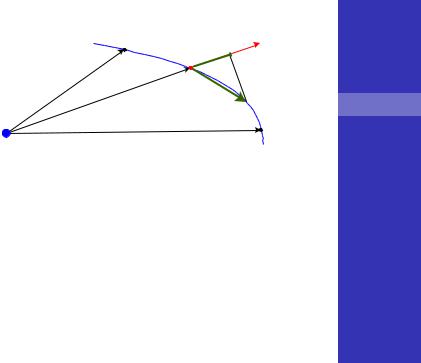
Работа на элементарном пути : |
|
|
|
|
|
|
|
|
|||||||||
|
|
1 |
|
′ |
|
1 |
|
′ |
| | = |
|
1 |
|
′ |
|
|||
= = |
4 0 |
|
3 |
= |
4 0 |
|
3 |
|
4 0 |
2 |
|
||||||
Работа силы Кулона зависит только от начальной и конечной точки и не зависит от формы траектории:
12 = ∫ |
2 |
|
2 |
2 |
= 4 0′ 1 |
− 4 0′ 2 |
||
= 4 ′0 |
∫ |
|||||||
|
|
|
|
|
|
|
|
|
11
Потенциал
электрического
поля
Примеры
применения теоремы Гаусса
Потенциал поля точечного заряда
Работа силы Кулона
Потенциальная
энергия
Понятие
потенциала
Единица
измерения
потенциала
Потенциал системы зарядов
Связь напряжённости и потенциала
Эквипотенциальны
поверхности
Циркуляции вектора
14/32
Потенциальная энергия
Электрическое поле центральное. Как и всякое центральное поле, оно консервативное, т. е. совершаемая им работа не зависит от формы траектории.
Работу сил консервативного поля можно представить как изменение потенциальной энергии:
12 = |
′ |
− |
′ |
= 1 − 2 |
4 0 1 |
4 0 2 |
|||
Потенциальная энергия заряда ′ |
в поле заряда : |
|||
= ′ + const 4 0
Положим const = 0. Тогда потенциальная энергия при удалении на бесконечность обращается в нуль.
Потенциал
электрического
поля
Примеры
применения теоремы Гаусса
Потенциал поля точечного заряда
Работа силы Кулона
Потенциальная
энергия
Понятие
потенциала
Единица
измерения
потенциала
Потенциал системы зарядов
Связь напряжённости и потенциала
Эквипотенциальны
поверхности
Циркуляции вектора
15/32
Потенциальная энергия
Электрическое поле центральное. Как и всякое центральное поле, оно консервативное, т. е. совершаемая им работа не зависит от формы траектории.
Работу сил консервативного поля можно представить как изменение потенциальной энергии:
12 = |
′ |
− |
′ |
= 1 − 2 |
4 0 1 |
4 0 2 |
|||
Потенциальная энергия заряда ′ |
в поле заряда : |
|||
= ′ + const 4 0
Положим const = 0. Тогда потенциальная энергия при удалении на бесконечность обращается в нуль.
Потенциал
электрического
поля
Примеры
применения теоремы Гаусса
Потенциал поля точечного заряда
Работа силы Кулона
Потенциальная
энергия
Понятие
потенциала
Единица
измерения
потенциала
Потенциал системы зарядов
Связь напряжённости и потенциала
Эквипотенциальны
поверхности
Циркуляции вектора
15/32

Потенциальная энергия
Электрическое поле центральное. Как и всякое центральное поле, оно консервативное, т. е. совершаемая им работа не зависит от формы траектории.
Работу сил консервативного поля можно представить как изменение потенциальной энергии:
12 = |
′ |
− |
′ |
= 1 − 2 |
4 0 1 |
4 0 2 |
|||
Потенциальная энергия заряда ′ |
в поле заряда : |
|||
= ′ + const 4 0
Положим const = 0. Тогда потенциальная энергия при удалении на бесконечность обращается в нуль.
Потенциал
электрического
поля
Примеры
применения теоремы Гаусса
Потенциал поля точечного заряда
Работа силы Кулона
Потенциальная
энергия
Понятие
потенциала
Единица
измерения
потенциала
Потенциал системы зарядов
Связь напряжённости и потенциала
Эквипотенциальны
поверхности
Циркуляции вектора
15/32

Потенциальная энергия
Электрическое поле центральное. Как и всякое центральное поле, оно консервативное, т. е. совершаемая им работа не зависит от формы траектории.
Работу сил консервативного поля можно представить как изменение потенциальной энергии:
12 = |
′ |
− |
′ |
= 1 − 2 |
4 0 1 |
4 0 2 |
|||
Потенциальная энергия заряда ′ |
в поле заряда : |
|||
= ′ + const 4 0
Положим const = 0. Тогда потенциальная энергия при удалении на бесконечность обращается в нуль.
Потенциал
электрического
поля
Примеры
применения теоремы Гаусса
Потенциал поля точечного заряда
Работа силы Кулона
Потенциальная
энергия
Понятие
потенциала
Единица
измерения
потенциала
Потенциал системы зарядов
Связь напряжённости и потенциала
Эквипотенциальны
поверхности
Циркуляции вектора
15/32

Понятие потенциала
Разные пробные заряды ′, ′′ имеют разную
потенциальную энергию. Отношение потенциальной энергии пробного заряда к величине заряда постоянно и называется потенциалом электрического поля:
= ′
Потенциал
поля в точке численно равен потенциальной энергии, которой обладает в этой точке единичный положительный заряд.
Потенциал поля точечного заряда:
= 1 4 0
Потенциал
электрического
поля
Примеры
применения теоремы Гаусса
Потенциал поля точечного заряда
Работа силы Кулона
Потенциальная
энергия
Понятие
потенциала
Единица
измерения
потенциала
Потенциал системы зарядов
Связь напряжённости и потенциала
Эквипотенциальны
поверхности
Циркуляции вектора
16/32

Понятие потенциала
Разные пробные заряды ′, ′′ имеют разную
потенциальную энергию. Отношение потенциальной энергии пробного заряда к величине заряда постоянно и называется потенциалом электрического поля:
= ′
Потенциал
поля в точке численно равен потенциальной энергии, которой обладает в этой точке единичный положительный заряд.
Потенциал поля точечного заряда:
= 1 4 0
Потенциал
электрического
поля
Примеры
применения теоремы Гаусса
Потенциал поля точечного заряда
Работа силы Кулона
Потенциальная
энергия
Понятие
потенциала
Единица
измерения
потенциала
Потенциал системы зарядов
Связь напряжённости и потенциала
Эквипотенциальны
поверхности
Циркуляции вектора
16/32

Понятие потенциала
Разные пробные заряды ′, ′′ имеют разную
потенциальную энергию. Отношение потенциальной энергии пробного заряда к величине заряда постоянно и называется потенциалом электрического поля:
= ′
Потенциал
поля в точке численно равен потенциальной энергии, которой обладает в этой точке единичный положительный заряд.
Потенциал поля точечного заряда:
= 1 4 0
Потенциал
электрического
поля
Примеры
применения теоремы Гаусса
Потенциал поля точечного заряда
Работа силы Кулона
Потенциальная
энергия
Понятие
потенциала
Единица
измерения
потенциала
Потенциал системы зарядов
Связь напряжённости и потенциала
Эквипотенциальны
поверхности
Циркуляции вектора
16/32

Заряд, находящийся в точке поля с потенциалом , обладает потенциальной энергией
=
Работа по перемещению заряда равна:
12 = ( 1 − 2) = − ,
ãäå = 2 − 1.
Если заряд переместили на бесконечность, то 2 = 0 (мы договорились так считать), тогда
∞ =
Потенциал
численно равен работе, которую совершают силы поля над единичным положительным зарядом при удалении его из данной точки на бесконечность.
Потенциал
электрического
поля
Примеры
применения теоремы Гаусса
Потенциал поля точечного заряда
Работа силы Кулона
Потенциальная
энергия
Понятие
потенциала
Единица
измерения
потенциала
Потенциал системы зарядов
Связь напряжённости и потенциала
Эквипотенциальны
поверхности
Циркуляции вектора
17/32

Заряд, находящийся в точке поля с потенциалом , обладает потенциальной энергией
=
Работа по перемещению заряда равна:
12 = ( 1 − 2) = − ,
ãäå = 2 − 1.
Если заряд переместили на бесконечность, то 2 = 0 (мы договорились так считать), тогда
∞ =
Потенциал
численно равен работе, которую совершают силы поля над единичным положительным зарядом при удалении его из данной точки на бесконечность.
Потенциал
электрического
поля
Примеры
применения теоремы Гаусса
Потенциал поля точечного заряда
Работа силы Кулона
Потенциальная
энергия
Понятие
потенциала
Единица
измерения
потенциала
Потенциал системы зарядов
Связь напряжённости и потенциала
Эквипотенциальны
поверхности
Циркуляции вектора
17/32

Заряд, находящийся в точке поля с потенциалом , обладает потенциальной энергией
=
Работа по перемещению заряда равна:
12 = ( 1 − 2) = − ,
ãäå = 2 − 1.
Если заряд переместили на бесконечность, то 2 = 0 (мы договорились так считать), тогда
∞ =
Потенциал
численно равен работе, которую совершают силы поля над единичным положительным зарядом при удалении его из данной точки на бесконечность.
Потенциал
электрического
поля
Примеры
применения теоремы Гаусса
Потенциал поля точечного заряда
Работа силы Кулона
Потенциальная
энергия
Понятие
потенциала
Единица
измерения
потенциала
Потенциал системы зарядов
Связь напряжённости и потенциала
Эквипотенциальны
поверхности
Циркуляции вектора
17/32

Заряд, находящийся в точке поля с потенциалом , обладает потенциальной энергией
=
Работа по перемещению заряда равна:
12 = ( 1 − 2) = − ,
ãäå = 2 − 1.
Если заряд переместили на бесконечность, то 2 = 0 (мы договорились так считать), тогда
∞ =
Потенциал
численно равен работе, которую совершают силы поля над единичным положительным зарядом при удалении его из данной точки на бесконечность.
Потенциал
электрического
поля
Примеры
применения теоремы Гаусса
Потенциал поля точечного заряда
Работа силы Кулона
Потенциальная
энергия
Понятие
потенциала
Единица
измерения
потенциала
Потенциал системы зарядов
Связь напряжённости и потенциала
Эквипотенциальны
поверхности
Циркуляции вектора
17/32

Единица измерения потенциала
Из формулы = можно получить единицу измерения потенциала:
[ ] =  = ÄæÊë
1В, вольт,
есть потенциал в такой точке поля, для перемещения из которой на бесконечность положительного заряда в 1Êë
нужно совершить работу в 1Äæ.
Потенциал
электрического
поля
Примеры
применения теоремы Гаусса
Потенциал поля точечного заряда
Работа силы Кулона
Потенциальная
энергия
Понятие
потенциала
Единица
измерения
потенциала
Потенциал системы зарядов
Связь напряжённости и потенциала
Эквипотенциальны
поверхности
Циркуляции вектора
18/32
