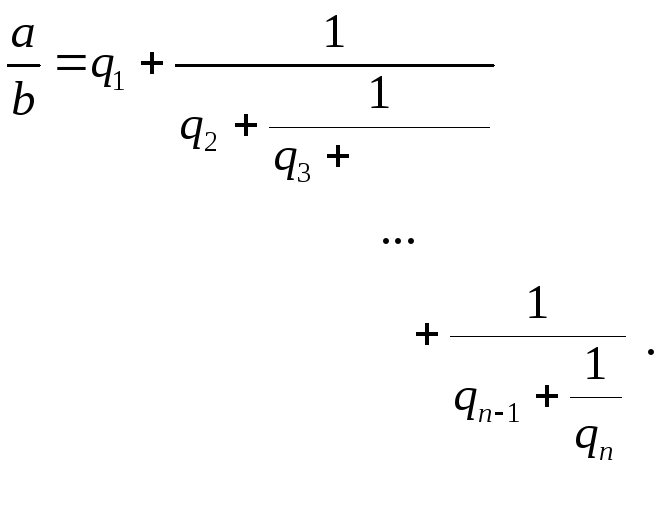Примеры для самостоятельного решения.

1. Найти остаток от деления на 11.

2. Найти последние две цифры числа .

3. Найти последние три цифры числа .

Конечные цепные дроби

1. Выделение целой части.

Пусть – целое,– натуральное число. Тогда существует единственное представление:

,, (1)

где – неполное частное– остаток отделенияна.

Формула (1) равносильна соотношению:

,. (2)

Из (2) видно, что . Значит,.

2. Разложение в конечную цепную дробь.

Пусть рациональное число, причем. Применяя ки алгоритм Евклида для определения их наибольшего общего делителя, получаем конечную систему равенств.

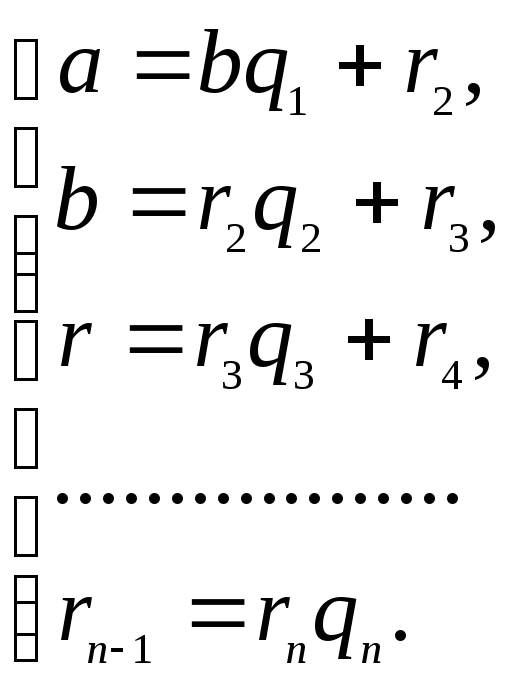
(1)

Системе равенств (1) соответствует равносильная система:

(2)

из которой последовательной заменой каждой из дробей , и т. д. ее соответствующим выражением из следующей строки получается представление дроби в виде

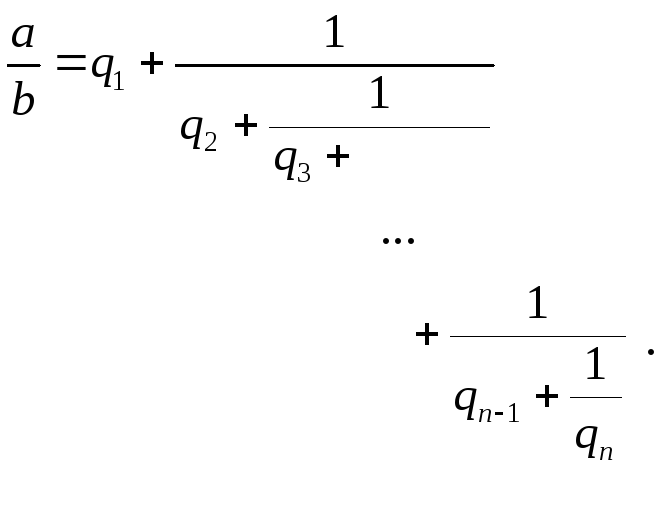
Такое выражение называется правильной конечной цепной дробью или правильной непрерывной дробью. При этом предполагается, что – целое, а– натуральные числа. Имеются различные формы записи цепных дробей:

1. 

2. 

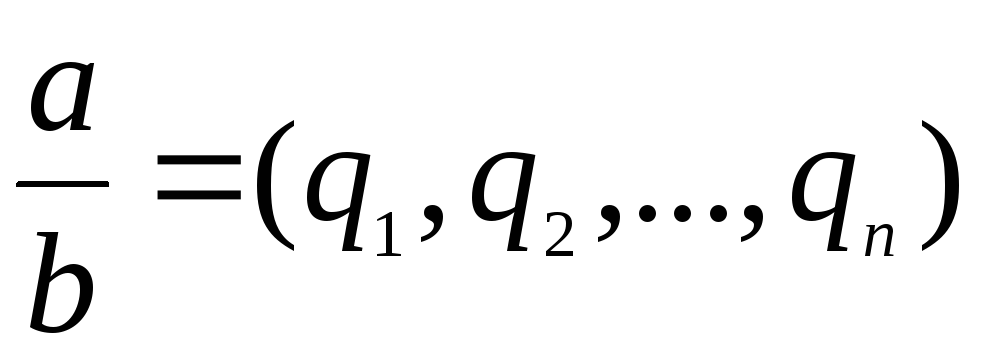3. и др.

Согласно последнему обозначению имеем

Числа – называются элементами цепной дроби.

Разложение рационального числа имеет, очевидно, конечное число элементов, так как алгоритм Евклида последовательного деленияa на b является конечным.

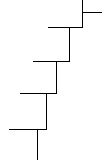
Пример.

Разложить данную обыкновенную дробь в непрерывную.

Решение.

0

Получаем

.

3. Подходящие дроби и некоторые их свойства.

Рассмотрим дроби вида

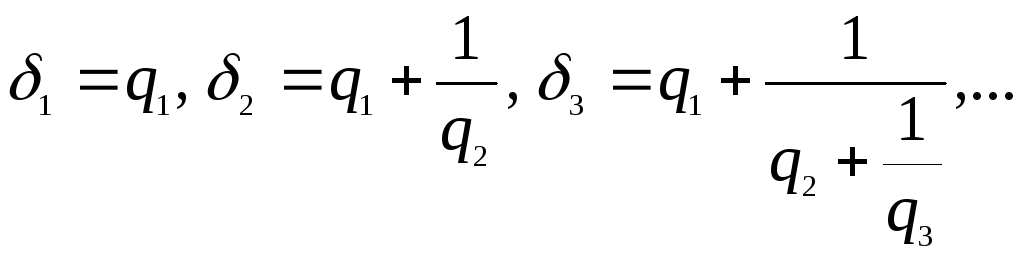
или

которые называются подходящими дробями данной непрерывной дроби или соответствующего ей числа . Заметим, что==.

Считается, что подходящая дробь имеет порядок. Заметим, чтопереходит в, если в первой заменитьвыражением.

Имеем,

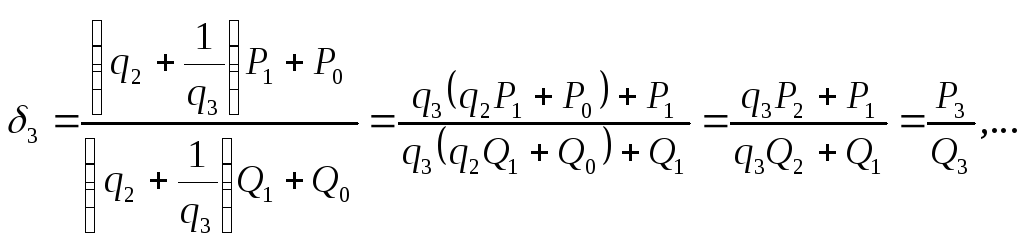
При этом принимается, что и т. д. Закономерность, которую мы замечаем в построении формулы для(ее числителяи знаменателя) сохраняется при переходе ки сохраняется также при переходе отк, поэтому на основании принципа математической индукции для любого, где, имеем

(1)

причем

и

Применяется следующая схема, в которую последовательно записываются значения , отдопо формулам (1).

Отметим некоторые свойства подходящих дробей.

1. Пусть 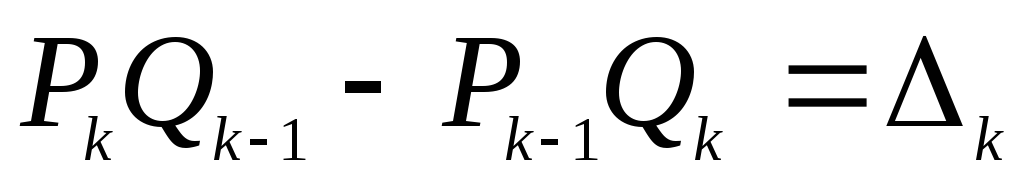. Так как по формулам (1)

то

.

Откуда видно, что все имеют одинаковые абсолютные значения, а их знаки чередуются. Но

поэтому для любого

(2)

Формула (2) показывает, что .

Так как если было бы , то получили бы противоречие, потому что из этого следовало бы, что, что невозможно. Значит все подходящие дробиявляются несократимыми.

2. При помощи формулы (2) легко установить разность двух соседних подходящих дробей. Действительно, так как

, то

(3)

Отсюда расстояние между двумя соседними подходящими дробями:

(4)

3. Между подходящими дробями и самой дробью 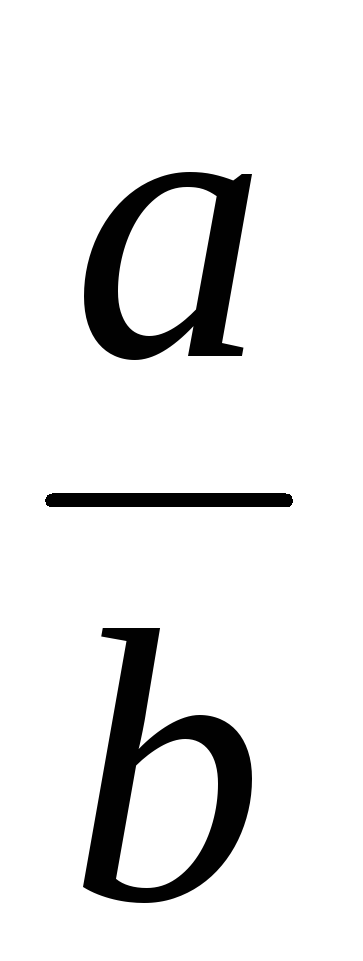справедливы соотношения:

Из этих соотношений видно, что дробь всегда заключена между двумя соседними подходящими дробями, интервал между которыми уменьшается по мере возрастания порядка. Этим и объясняется название «подходящие» дроби.

4. Решение сравнений первой степени с помощью цепных дробей.

Рассмотрим сравнение

(1)

где (случайсводится к данному).

Разложим в непрерывную дробь и обозначим ее подходящие дроби через, где

Тогда, согласно свойству несократимости подходящих дробей, получим Поэтому вместо соотношения

Имеем ,

Отсюда

,

или (так как – целое число)

Умножая обе части этого сравнения на , получим

Сравнивая это сравнение с исходным (1), приходим к выводу, что оно имеет решение

(2)

где – числитель предпоследней дроби в разл

26