§ 8. Повторение испытаний. Формула бернулли.

Пусть произведено испытаний. Если вероятность собы -тияв каждом испытании не зависит от результатов других испытаний, то такие испытания называютсянезависимыми от– носительно события

Для серии таких испытаний может быть поставлена следу -ющая задача: определить вероятность того, что в результате проведения независимых испытаний, в которых событиепоявляется с постоянной вероятностью, событиепроизойдёт ровнораз, т.е. найти

При условии можно было бы воспользоваться теоремами сложения и умножения вероятностей с исполь- зованием правил сложения и уножения вероятностей событий. Но, по мере увеличения числа испытаний, эти правила приводят к громоздким формулам и, с учётом перебора возможных вариантов, к не менее громоздким вычислениям.

Более простой способ вычисления таких вероятностей осно- ван на применении формулы Бернулли.

Пусть в одинаковых условиях производится независимых испытаний, в каждом из которых событиепоявляется с по- стоянной вероятностью, а противоположное собы -тиес вероятностью.

Пусть - появления событияв- м испытании ().

Рассмотрим такое событие: в испытаниях первыераз событиепоявилось, а потом перестало появляться, т.е. со- бытие. Так как входящие в собы -тиесобытия независимы, то

Но комбинаций, типа комбинации , существует( т.е. столько есть способов расставить «чёрточек надмножи - телями»), причём все такие комбинации несовместны. Поэтому

. (1)

Полученная формула называется формулой Бернулли.

Пример 1. В среднем пятая часть поступающих в продажу автомобилей некомплектна. Найти вероятность того, что среди 10 – ти прибывших автомобилей имеют некомплектность: а) три автомобиля; б) хотя бы три.

Событие - автомобиль имеет некомплектность. Тогда, по условию,

а) По формуле (1),

б) Событие - «хотя бы три автомобиля некомплектны», те. от 3 – х до 10 – ти. Его вероятность проще искать через вероятность противоположного событие- «менее 3 – х ав- томобилей некомплектны».

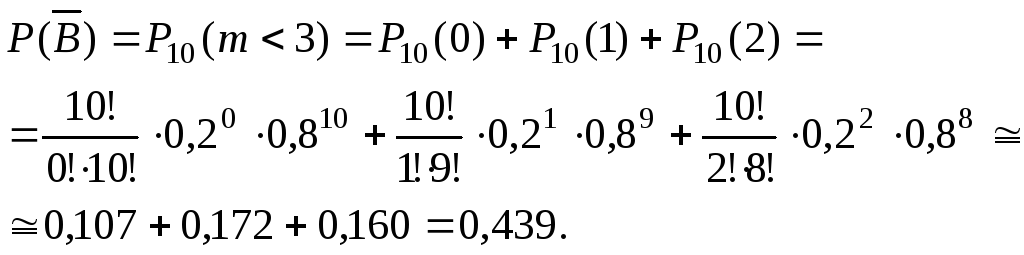Тогда

Так как события, состоящие в различном числе появлений события в серии изнезависимых испытаний образуют полную группу несовместных событий, то сумма их вероят -ностей равна единице, т.е.

Эта сумма представляет собой разложение - й степени бинома (бином Ньютона) и связанное с ней распределение вероятностей числа появлений событияв серии изопытов называетсябиномиальным распределением.

Учмтывая это, для вычисления вероятностей возможного числа появлений события в серии изнезависимых ис- пытаний можно ввести так называемуюпроизводящую функ- цию :

Эта функция обладает тем свойством, что коэффициент, стоя- щий перед в этой сумме равен вероятности.

Пример 2. Предполагается, что в среднем 20% открываю –щихся малых предприятий разоряются в течение года. Найти вероятность того, что после года работы из 6 – ми вновь от - крывшихся предприятий не разорится: а) ровно 5; б) хотя бы четыре.

Вероятность того, что предприятие разорится , со - ответственно, вероятность того, что оно не разорится, равнаДля решения воспользуемся производящей функцией.

Непосредственным сложением можем проверить, что сумма всех коэффициентов в этом разложении равна 1. Тогда, в случае а): , т.е. коэффициент, стоящий перед. В случае б):, т.е. сумма коэффициен- тов, стояший перед.

Аналогичную производящую функцию можно ввести и для случая, когда в серии из испытания вероятности появления события в каждом испытании различны. Пусть вероятность по- явления события в испытании равнаи, соот- ветственно, вероятность того, что событие не произошло -. Тогда о вероятностях определённого числа появлений событияв данной серии опытов можно судить по значению коэф -фициентов перед определёнными степенямив разложении по степенямследующей производящей функции:

.

Пример 3. Пусть пять баскетболистов бросили по одному разу мяч в корзину. Найти вероятность того, что будет три точных попадания, если для 1 – го и 3 – го вероятности попа -дания равны 0,7, для 2 –го - 0,6, для 4 – го - 0,8 и для 5 – го - 0,9.

В этих условиях, ,

Тогда производящая функция имеет вид:

Сумма коэффициентов в разложении равна единице.

Тогда вероятность того, что будет три попадания мяча в кор- зину равна коэффициенту перед , т.е.

Если бы мы искали эту вероятность, применяя теоремы сло- жения и умножения вероятностей, то вычисления были бы на- много более громоздкими.

Определение. Наивероятнейшим числом появлений со- бытияв серии изнезависимых испытаний называется число, для которогоявляется наибольшим.

Например, в примере 2, ; в примере 2 ,.

Используя формулу Бернулли, можно вывести формулу для нахождения наивероятнейшего числа появлений события:

(2)

Замечание. Длина промежутка, определяемого этими нера- венствами равна единице:, поэтому, если границы промежутка дробные, тоопределяется однозначно, если же целые - получаем два значения для.

Пример 4. Вероятность попадания в мишень при каждом выстреле равна 0,7. Найти наивероятнейшее число попаданий в мишень при 8 – ми выстрелах и определить вероятность такого числа попаданий.

В этом примере Тогда

Теперь найдём вероятность: