§ 4 Основные законы распределения

СЛУЧАЙНЫХ ВЕЛИЧИН

Сначала рассмотрим некоторые законы распределения дис- кретных случайных величин.

0. 4.1 Биномиальное распределение .

Пусть случайная величина - это число появлений неко -торого событияв серии изнезависимых испытаний, в каждом из которых вероятность появления события, а вероятность не появления событияРяд распределения такой величины имеет вид:

	0	1

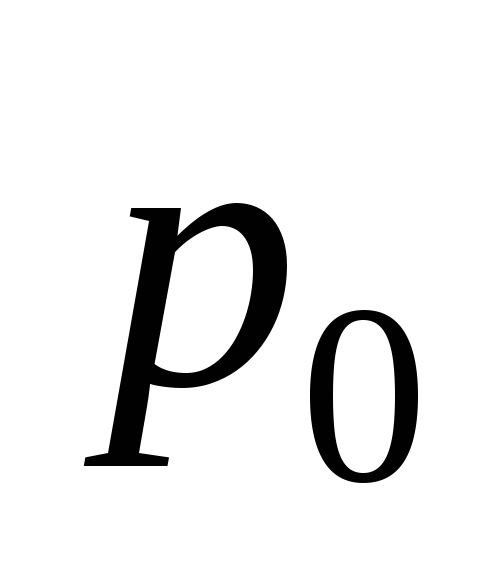
где . Такой ряд распределения называетсябиномиальным. Математическое ожидание случайной величины в этом случае имеет вид:

(1)

Для вычисления этого выражения, продифференцировав по следующее выражение:получим

Если мы умножим это равенство на , получим

(2)

Но а правые части равенств (1) и (2) совпадают, тогда

Продифференцировав то же самое выражение дважды, получим

Умножив полученное равенство на , получим:

Тогда

Таким образом,

Отсюда Тода

Итак, для биномиального распределения:

Пример. Произведено 20 независимых выстрелов по мише- ни. Вероятность попадания при каждом выстреле . Найти математическое ожидание, дисперсию и среднее квад -ратическое ожидание числа попаданий.

Случайная величина - число попаданий, распределена по биномиальному закону.Тогда

0. 4.2 Распределение Пуассона.

Определение. Дискретная случайная величина имеет

закон распределения Пуассона, если она задаётся рядом рас- пределения

	0	1

в котором вероятности определяются по формуле Пуассона

(3)

где (- среднее число появлений события в серии испытаний, в каждом из которых вероятность появления события постоянная величина).

Приведём без доказательства следующую теорему.

ТЕОРЕМА. Математическое ожидание и дисперсия случай -ной величины, распределённой по закону Пуассона, совпадают и равны параметру этого закона, т.е.

При достаточно больших (вообще при) и малых значенияхпри условии, что произведение- постоянная величина (), закон распределения Пуассона является хорошим приближением биномиального за –кона, т.е. распределение Пуассона - это асимптотическое рас -пространение биномиального закона. Иногда этот закон назы -ваютзаконом редких явлений. По закону Пуассона распреде- лены, например, число сбоев автоматической линии, число от- казов системы в «нормальном режиме», число сбоев в работе АТС и т.п.

0. 4.3 Геометрическое распределение.

Определение. Дискретная случайная величина име- етгеометрическое распределение, если , где для некоторого события,

и её ряд распределения имеет вид:

	1	2

В этом случае вероятности представляют собой бесконечно убывающую геометрическую прогрессию и её сумма

.

ТЕОРЕМА. В случае случайной величины, имеющей геомет- рическое распределение с параметром , математическое ожидание и дисперсия вычисляются по формулам:

Пример. Производятся выстрелы по мишени до первого попа- дания. Вероятность попадания при каждом выстреле .

Составить ряд распределения случайной величины - «чис- ло попаданий». Найти её математическое ожидание и среднее квадратическое отклонение.

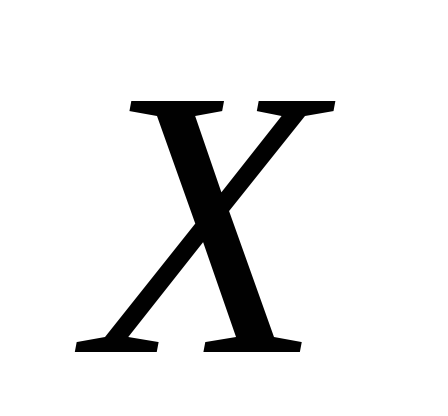
	1	2	3

По теореме,

среднее квадратическое отклонение

0. Гипергеометрическое распределение.

Пусть в партии из изделий имеетсястандартных. Случайным образом отбираютизделий. Пусть случайная величина- число стандартных изделий среди отобранных. Очевидно, озможные значения этой случайной величины:

Вероятности возможных значений вычисляются по формуле:

Для этой случайной величине математическое ожидание вы- числяется по формуле а дисперсия:

Пример. В урне находится 5 белых и 3 чёрных шара. Слу- чайным образом отобраны 3 шара. Составить ряд распределе- ния случайной величины - числа белых шаров среди ото –бранных. Найти её математическое ожидание и дисперсию.

Возможные значения этой случайной величины: 0, 1, 2, 3. найдём их вероятности:

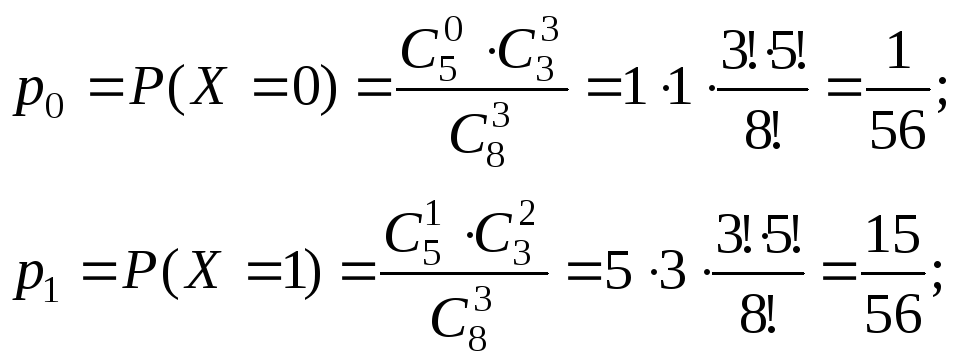
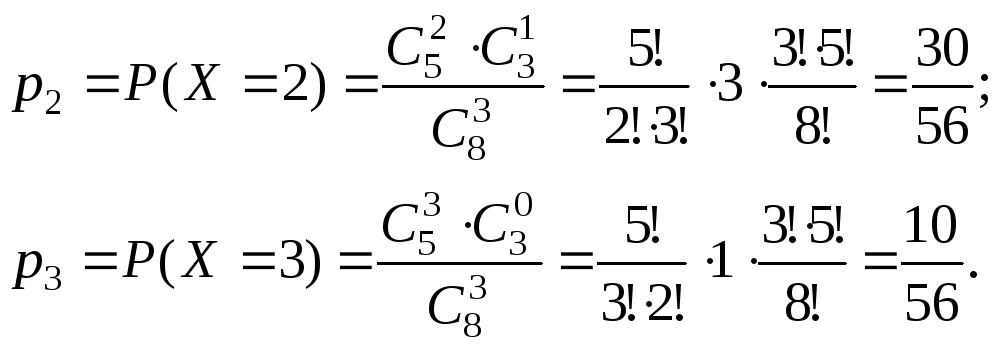
Получаем ряд распределения:

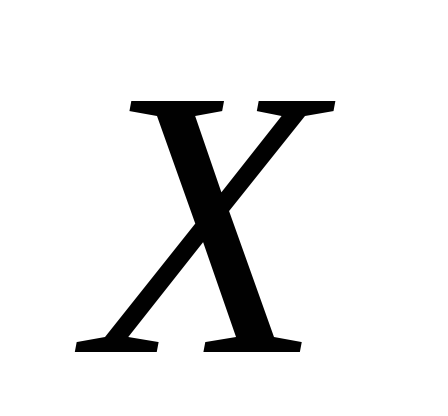
	0	1	2	3

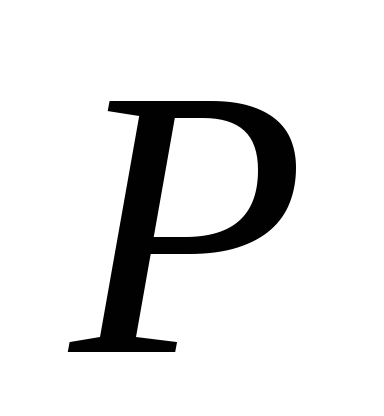
Математическое ожидание можно вычислить непосредственно, пользуясь известными формулами, а можно воспользоваться формулами из теоремы. В нашем примере

. Тогда

Теперь рассмотрим основные законы распределения непре- рывных случайных величин.

0. 4.5 Равномерное распределение.

Определение. Непрерывная случайная величина имеет рав -номерное распределение на отрезке , если она имеет постоянное значение на этом отрезке и равна нулю вне этого отрезка, т.е. график её плотности имеет вид:

С

Так как площадь под графиком плотности распределения должна быть равна единице, то Тогда

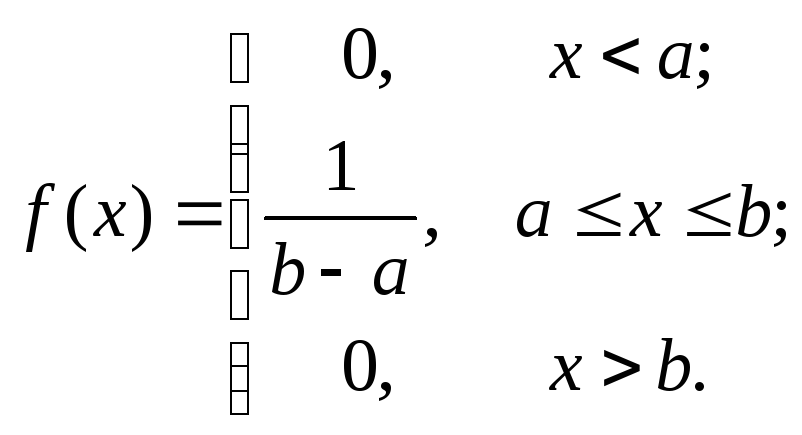
Её функция распределения имеет вид:

и её график

1

0. 4.6 Показательное распределение.

В практических приложениях теории вероятностей (напри-

мер, в сфере массового обслуживания, исследовании опера -ций, теории надёжности, в физике, биологии и т.п.) часто при- ходится иметь дело со случайными величинами, имеющими так называемое экспоненциальное, или показательное распре- деление.

Определение. Непрерывная случайная ыеличина рас- пределена попоказательному закону , если её плотность распределения вероятностей имеет вид:

График этой функции:

0

Её функция распределения:

имеет график

1

О

Математическое ожидание:

Пример. Пусть случайная величина - время работы не- которого механизма, имеет показательное распределение. Оп- ределить вероятность того, что механизм будет работать не менее 1000 часов, если среднее время его работы составляет 800 часов.

По условию задачи, математическое ожидание работы меха- низма , а. Тогда

Следовательно,

Искомая вероятность:

Замечание. Показательное распределение относится к од -нопараметрическим законам распределения (зависит только от ).

0. 4.7 Нормальное распределение.

Определение. Нормальным называют распределение вероят- ностей непрерывной случайной величины, которое имеет плот- ность распределения вероятностей, определяемую формулой:

(1)

Видим, что нормальное распределение определяется двумя параметрами : и. Чтобы задать нормальное распре -деление, достаточно задать эти два параметра.

Нормальный закон распределения очень широко распро- странён в задачах практики. Он проявляется в тех случаях, когда случайная величина является результатом действи- ем большого числа различных факторов. Каждый фактор в отдельности влияет на случайную величину незначительно и нельзя сказать, какой из них влияет в большей степени, чем остальные. Примерами случайных величин, имеющих нормаль- ное распределение, можно считать: отклонение размеров дета- лей, изготовленных станком, от стандартных; ошибки при из -мерении; отклонения при стрельбе по мишени и т.п.

Основной закономерностью, выделяющей нормальный закон из остальных законов, является та, что он является предель -ным законом, к которому приближаются другие законы, т.е. при достаточно большом значении сумма независимых слу- чайных величин, подчинённых каким угодно законам распределения, будет иметь распределение, сколь угодно близкое к нормальному.

Функция распределения нормально распределённой случай –ной величины имеет вид

(2)

По определению математического ожидания непрерывной случайной величины,

Введём новую переменную

Принимая во внимание, что новые пределы интегрирования равны старым, получим

Первой слагаемое равно нулю, как интеграл по симметрич -ному промежутку от нечётной функции. Второе из слагаемых равно (интеграл Пуассона).

Таким образом, математическое ожидание нормально рас- пределённой случайной величины

По определению дисперсии непрерывной случайной величи- ны, учитывая, что , получим

Снова введём новую переменную

Получим Применив формулу интегрирования по частям и предыдущие вычисления, получа- емТогдаСледовательно, вторым параметром нормального распределенияявляется сре- днее квадратическое отклонение.

Замечение. Нормированным называют нормальное распре –деление с параметрами Плотность нормиро -ванного распределения задаётся функцией:

(3)

значения которой можно либо найти непосредмьвенно, либо воспользоватся соответствующими таблицами, которые можно найти во всех справочниках. Функция нормированного распре –деления имеет вид . Тогда функция общего нормального распределения, заданная т формулой (2), выражается формулой. Вероятность попа- дания нормированной нормально распределённой случайной величиныв интервалопределяется с помощью функции Лапласа, значения которой также приведены в таблицах. В самом деле,

Учитывая, что (по свойству плотности распре- деления,), в силу симметрии функцииотносительно точ- ки:

Тогда

График плотности нормального распределения называют нормальной кривой или кривой Гаусса.

Исследуем функцию:

Она определена на всей числовой прямой и положительна для всех . При неограниченном возрастанииданная функция стремится к нулю, т.е.Производная этой функции.

Производная равна 0 в точке и меняет в этой точке знак с «+» на «-», т.е.- точка максимума и в этой точке. Найдя вторую производную функции, можем выяснить, что график функции имеет перегибы в точ- ках. Схематически график выглядит следующим образом:

0

Для нормально распределенной случайной величины ве- роятность попадания в заданный интервал вычисля –ется следующим образом:

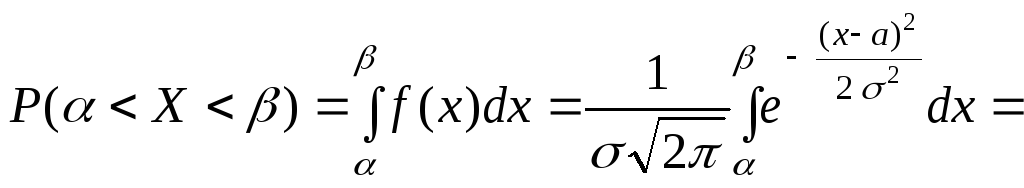
Сделаем замену .

где .

Таким образом,

(4)

Пример. Масса вагона - случайная величина, распределён -ная по нормальному закону с математическим ожиданием 65 т. и средним квадратическим отклонением т. Найти веро- ятность того, что очередной вагон имеет массу не более 70 т. и не менее 60 т

Тогда

Иногда требуется вычислить вероятность того, что случай -ная величина по модулю отклоняется от среднего значения меньше чем некоторое значение , т.е.. Для вычисления этой вероятности можем воспользоваться предыдущей формулой. В самом деле:

учитывая нечётность функции . Следовательно,

(5)

Пример. Вероятность того, что нормально распределённая случайная с математическим ожиданием откло- нится от среднего значения меньше чем наравна 0.09. Чему равна вероятность попадания этой случайной величины в интервал (30, 35) ?

По условию, ТогдаПо таблице значений функции Лапласа, по – лучаем:Тогда требуемая вероятность , по формуле (4),

Правило трёх сигм.

В формуле (5) положим , получим

Если и, следовательно,, получаем:

т.е. вероятность того, что отклонение по абсолютной величине случайной величины от среднего значения меньше утроенного среднего квадратического отклонения равна 0,9973, т.е. очень близка к единице.

Правило трёх сигм состоит в том, что для нормально рас- пределённой случайной величины абсолютная величина её -отклонения от среднего не превосходит утроенного сред -него квадратического отклонения. На практике это правило применяется слудующим образом: Если распределение слу -чайной величины неизвестно, но для её параметров выпол -няется правило трёх сигм, то есть основание предположить, что она распределена по нормальному закону.