§ 5 Аксиоматическое построение теории

ВЕРОЯТНОСТЕЙ.

Теория вероятностей, как и любая другая математическая наука, строится на основе некоторой системы аксиом. Исходя из статистического определения вероятности, аксиоматику не -обходимо вводить таким образом, чтобы она достаточно хоро- шо согласовывалась с опытом, т.е. вероятность события долж- на обладать свойствами частоты. Поэтому основные аксиомы:

Аксиома 1. Вероятность события - это неотрицательное число, заключённое между 0 и 1, т.е.

Аксиома 2. Вероятность достоверного события равна 1, т.е.

Аксиома 3. Вероятность невозможного события равна 0,

Замечание. Если вероятность некоторого события равна нулю, то это ещё не означает, что данное событие невоз -можно. Например, при выстреле по некоторой мишени, вероят- ность попадания в определённую точку равна нулю, но это ещё не означает, что данное событие невозможно. Просто ми- шень содержит бесконечно много точек. Точно также, если ве- роятность события равна 1, это ещё не означает, что оно дос- товерно. (Если в рассмотренном примере: А - «попадание в некоторую точку мишени», то , а, но- не достоверное событие.)

Аксиома 4 (аксиома сложения вероятностей). Вероят -ность суммы двух несовместных событий равна сумме их ве- роятностей:

Определение Вероятность появления события , вычис -ленная при условии появления другого события, скажем, называетсяусловной вероятностью и обозначается .

Аксиома 5 (аксиома умножения вероятностей). Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, т.е.

Следствие. На основании этой аксиомы, условную вероят -ность события можно искать по формуле .

Эти аксиомы уже позволяют решать некоторые простейшие задачи.

Пример 1. Из урны, содержащей 10 занумерованных шаров, необходимо извлечь шар с номером, кратным 3 или 4. События: - «номер шара делится на 3» = «3, 6, 9» и

- «номер шара делится на 4» = «4, 8».

Эти события несовместны. По

аксиоме 4, .

Пример 2. Из урны, содержащей 6 белых и 4 чёрных шара, поочерёдно (без возвращения) извлекают два шара. Найти ве- роятность того, что оба извлечённых шара белые. А - первый шар белый, В - второй шар белый. Тогда

.

§ 6 Теоремы сложения и умножения вероятно -

СТЕЙ.

С помощью метода математической индукции, аксиому сло- жения вероятностей можно обобщить на случай произвольного конечного числа несовместных событий :

Теорема. (теорема о сложении вероятностей несовместных событий) Вероятность появления хотя бы одного из не- совместных событий равна сумме их вероятностей:

Приведём важные следствия этой теоремы:

Следствие 1. Если события образуют пол -ную группу несовместных событий, то сумма их вероятностей равна единице, т.е.

В самом деле, в этом случае и

Следствие 2. Сумма вероятностей противоположных событий равна единице, т.е.

В самом деле, противоположные события несовместны и их сумма

Для случая бесконечного числа событий:

Аксиома 6. Вероятность суммы бесконечно большого числа несовместных событий равна сумме вероятностей этих собы –тий

Аксиому умножения вероятностей также, с помощью метода математической индукции, можно обобщить на случай произ - вольного конечного числа множителей .

Теорема. (об умножении вероятностей) Вероятность произ -ведения, или совместного появления событий равна произведению вероятности одного из них на условные вероятности остальных событий, вычисленные при условии, что все предшествующие события имели место, т.е.(1)

Пример. Пусть механизм состоит из 3 – х деталей. Работа механизма нарушается, если все эти детали больше, чем по- ложено по стандарту. У сборщика осталось 8 деталей, из ко- торых 4 увеличенного размера. Найти вероятность того, что собранный из оставшихся деталей механизм не будет рабо -тать.

- ненормальная работа механизма, ,- я деталь имеет больший размер. Тогда

Введём понятия зависимых и независимых событий.

Рассмотрим опыт из примера 2 предыдущего параграфа, но произведём его следующим образом: извлекаем один шар из урны с 6 – ю белыми и 4 – мя чёрными шарами, определяем его цвет, возвращаем его в урну, перемешиваем шары и снова извлекаем один шар. При тех же обозначениях вероятность того, что оба шара белые, равна

.

Здесь мы столкнулись с понятием независимых событий.

Определение. Событие называетсянезависимым по отношению к событию , если ероятность событияне зависит от того, произошло событиеили нет, т.е.. В противном случае, событиеназываетсязависимым от события .

В примере 2 предыдущего параграфа событие зависело от события( в урне изменилось количество шаров ). В примере, рассмотренном выше, при повторном извлечении шара начальные условия не изменились, поэтому вероятность событияне зависит от того, произошло событиеили нет, т.е. событиене зависит от события.

Замечание. Если событие не зависит от события, то и событиене зависит от события.

В самом деле, из аксиомы 5,

Но . Тогда

Определение. Два события называются независимыми, если появление одного из них не меняет вероятность появления другого.

Понятие независимости можно распространить на случай произвольного числа событий.

Определение. Несколько событий называются независимыми в совокупности если каждое из них и любая комбинация ос -тальных событий являются независимыми.

Например, события независимы в совокупности, если независимы друг относительно друга следующие события:

Следствие (теоремы об умножении вероятностей). Вероятность произведения независимых в совокупности собы -тий равна произведению их вероятностей, т.е.

(При условии независимости событий, условные вероятности в формуле (1) меняются на безусловные вероятности, в соответ-ствии с условием независимости событий).

Пример 1. Произведено 3 выстрела по удаляющейся мише -ни. Вероятность попадания при первом выстреле (событие ) равна 0,9, при втором (событие) - 0,7, при третьем (собы- тие) - 0,5. Найти вероятности следующих событий:- «все три попадания»;- «ровно два попадания»;- «толь- ко одно попадание»;- «по крайней мере два попадания»;- «хотя бы одно попадание»;- «ни одного попадания» (предполагается, что исходы всех выстрелов независимы друг от друга). Следовательно,Аналогично,

В данных условиях, . Событиянезависимы. Тогда

Событие . Все слагаемые, входящие в событие- несовместны, а множи -тели слагаемых - независимы. Поэтому

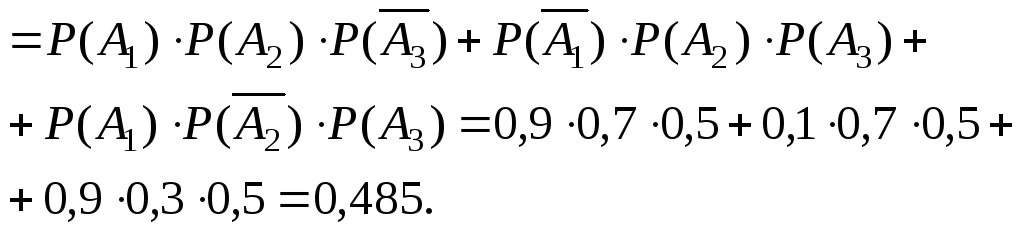
Событие

.

Событие:

,

Событие можно представить двумя способами: либо

и тогда его вероятность равна

, либо , тогда, учитывая следствие 2 теоремы о сложении вероятнос -тей,

Двумя способами получили тот же результат.

Пример 2. 5 раз подбрасывается монета. Найти вероят –ность того, что все 5 раз она выпадет одной и той же сто- роной (событие ), либо все 5 раз выпадет герб (событие), либо все 5 раз выпадет цифра (событие).. Со -бытияинесовместны. Поэтому.

Подбрасывания монеты считаем независимыми. Вероятность появления герба (цифры) при каждом подбрасывании равна 0,5. Тогда

Теорема. (теорема о сложении вероятностей совместных со- бытий) Вероятность появления хотя бы одного из двух сов- местных событий равна сумме их вероятностей без вероят -ности их совместного появления, т.е.

Д о к а з а т е л ь с т в о. Рассмотрим рисунок:

События иможно представить следующим обра- зом:. Слагаемые, входящие в эти события, являются несовместными. По правилу сложения вероятностей несовместных событий (ак- сиома 4 ), получаем:

Поэтому, так как

получаем

Теорема доказана.

Замечание. Если искать вероятность суммы трёх совмест -ных событий, то получим формулу:

По мере увеличения числа слагаемых формула сложения ве -роятности совместных событий довольно быстро разрастается и приводит к громоздким вычислениям, что очень неудобно. Поэтому при вычислении верояности суммы нескольких сов -местных событий целесообразно использовать понятие веро -ятности противоположного события. Если событие - «появ- дение хотя бы одного из совместных событий», т.е., то вероятность этого события мож- но вычислить следующим образом:

Это формула вычисления вероятности появления хотя бы одного из совместных событий.

Пример 1. Два раза подбрасывается игральный кубик. Найти вероятность того, что хотя бы один раз выпадет цифра 5.

- цифра 5 при первом подбрасывании. - цифра 5 при втором подбрасывании.Тогда, по теореме,

Другим способом, . Тогда

Получили тот же результат.

Пример 2. Произведено 3 выстрела по удаляющейся мише - ни. Вероятность попадания при первом выстреле (событие ) равна 0,9, при втором (событие) - 0,7, при третьем (собы- тие) - 0,5. Найти вероятность хотя бы одного попадания в мишень.

Воспользуемся формулой