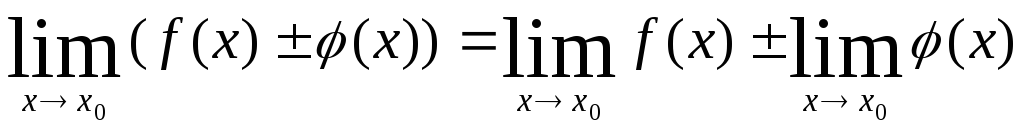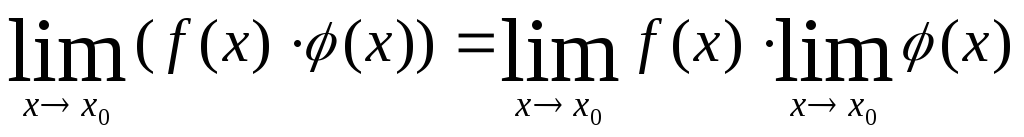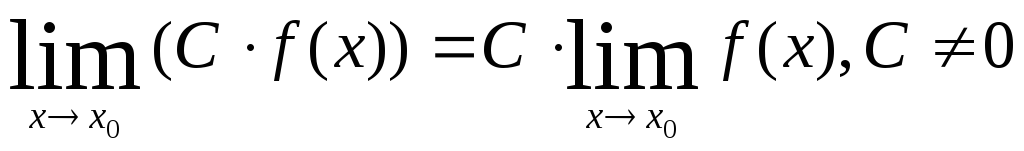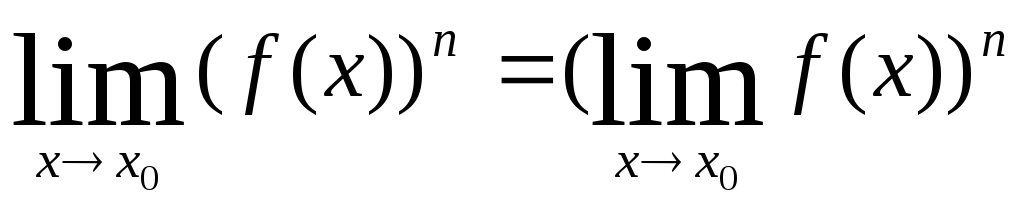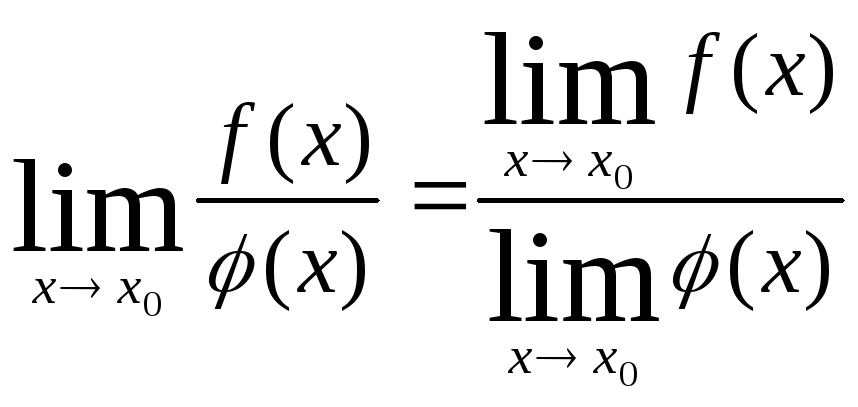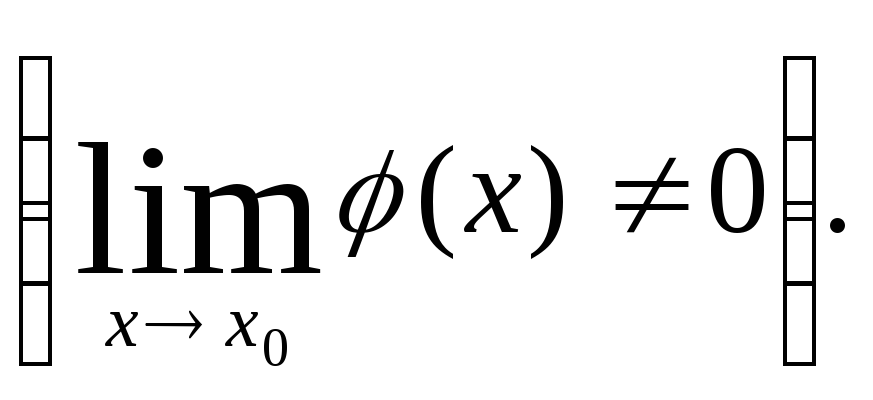II. Предел функции. Непрерывность функции

2.1. Понятие предела функции

Число А называется пределом функции в точке х₀ (или при хх₀), если для любого положительного числа найдется такое положительное число , что для всех хх_0, удовлетворяющих неравенству , выполняется неравенство.

Обозначают

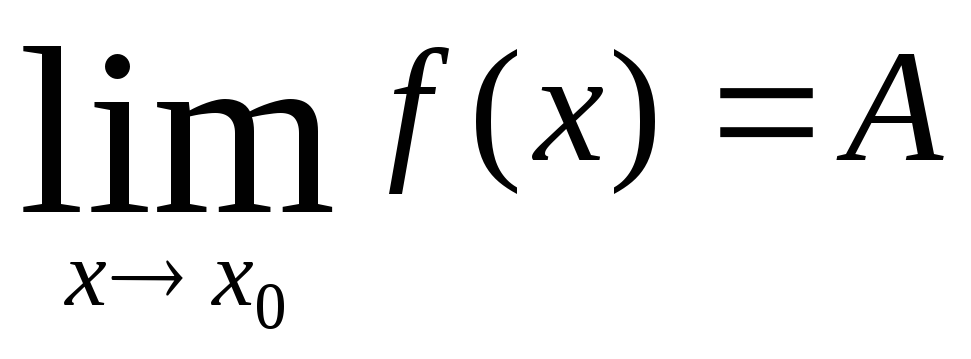
2.2. Бесконечно малые и бесконечно большие функции

Функция называетсябесконечно малой при , если .

Функция называетсябесконечно большой при , если или .

2.3. Теоремы о пределах

1. 

2. 

3. 

4. 

5. 

Первый замечательный предел

Второй замечательный предел

Правило Лопиталя.

Пусть функции инепрерывны и дифференцируемы в окрестности точкиx₀ и обращаются в нуль в этой точке: . Пустьв окрестности точкиx₀. Если существует предел 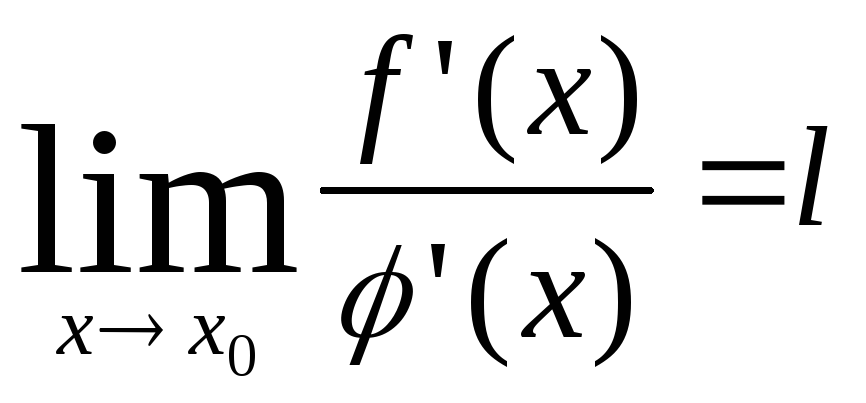, то.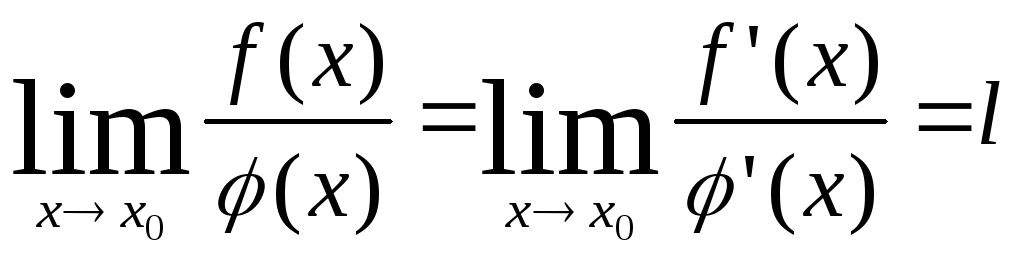

2.4. Односторонние пределы

Бывают случаи, когда способ приближения аргумента х к х₀ существенно влияет на значение предела функции. Поэтому вводят понятия односторонних пределов.

Число А₁ называется пределом функции y= f(x) слева в точке х₀, если для любого числа существует числотакое, что при хвыполняется неравенство. Предел слева записывают так: 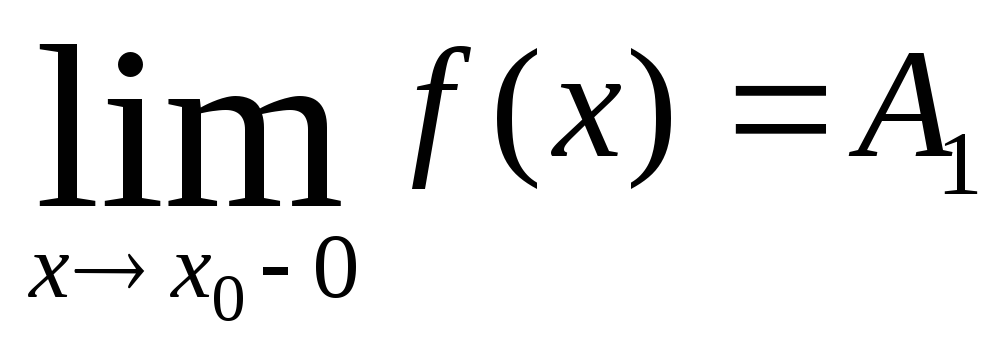или коротко: (обозначение Дирихле).

Аналогично определяется предел функции справа. Число А₂ называется пределом функции y= f(x) справа в точке х₀, если для любого числа существует числотакое, что при хвыполняется неравенство. Предел справа записывают так: 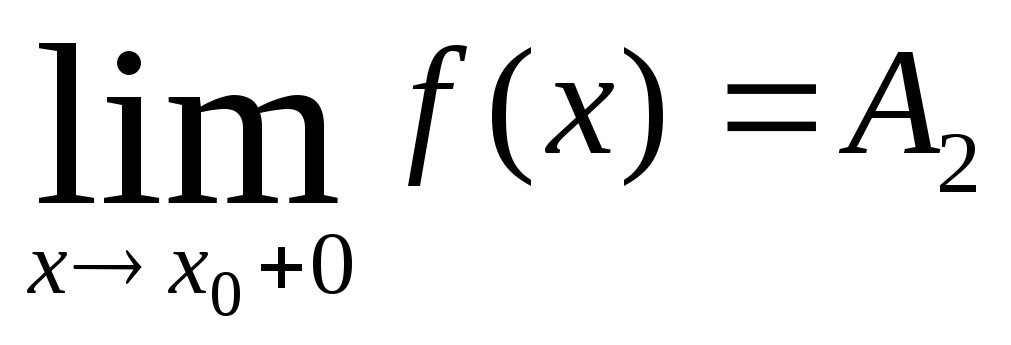. Коротко предел справа обозначают f(x_o+0)=A₂.

Пределы функции слева и справа называются односторонними пределами.

2.5. Непрерывность функции

Функция называетсянепрерывной в точке , если предел функции приравен значению функции при:

.

А также говорят, функция называетсянепрерывной в точке , если она в этой точке определена, и бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, т. е.

.

Существует теорема о непрерывности функции в точке. Функция y= f(x) непрерывна в точке x₀, тогда и только тогда, когда функция имеет конечные пределы в точке x₀ и предел функции в точке x₀ равен значению функции в этой точке.

Все элементарные функции непрерывны в области своего определения.

Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции.

Для элементарных функций справедливы следующие положения:

1. область непрерывности элементарной функции совпадает с её областью определения, т.е. элементарная функция непрерывна во всей области определения

2. элементарная функция может иметь разрыв только в отдельных точках какого-либо промежутка, но не во всех его точках

3. элементарная функция может иметь разрыв только в той точке, в которой она не определена.

Функция называется непрерывной в промежутке (замкнутом или открытом), если она непрерывна во всех точках этого промежутка.

Все точки разрыва функции разделяются на точки разрыва первого и второго рода.

Точка разрыва х₀ называется точкой разрыва первого рода функции , если в этой точке существуют конечные пределы функции слева и справа (односторонние пределы), т.еи.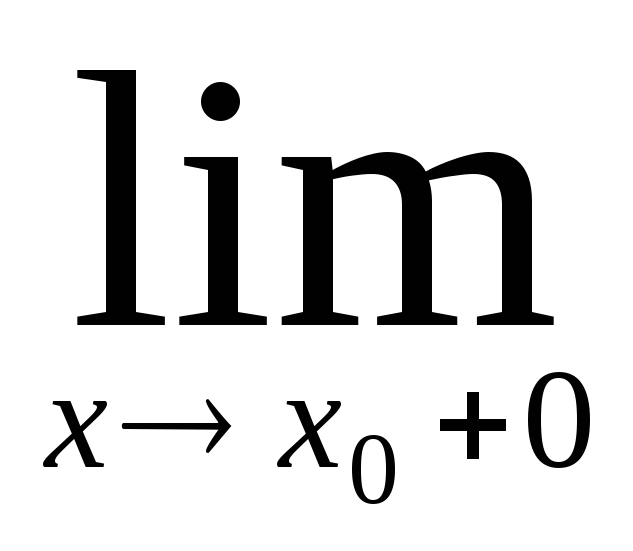

При этом:

если А₁=А₂, то точка х₀ называется точкой устранимого разрыва (рис.6)

если , то точка х₀ называется точкой конечного разрыва( рис.7).

Величину называютскачком функции

Рис. 6. График функции с устранимым разрывом

Рис. 7. График функции с конечным разрывом

Точка х₀ называется точкой разрыва 2-го рода, если по крайней мере один из односторонних пределов не существует или равен ∞ (рис.8).

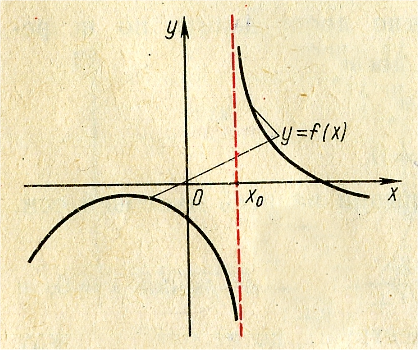
Рис. 8. График функции с точкой разрыва 2-го рода

Вычисление предела функции методом непосредственной подстановки

Примеры:

1. Найти

Решение:

1 способ.

Применяя теоремы о пределах с последующей подстановкой предельного значения x=1 запишем:

2 способ.

Поскольку исходная функция есть алгебраическая сумма элементарных функций, непрерывных в области определения, а, следовательно, и при x=1, то согласно определению непрерывности функции имеем

Ответ:

2. Найти

Решение:

При x→3 числитель дроби стремится к числу 4, а знаменатель к числу 2.

Следовательно, применяя теоремы о пределах с последующей подстановкой предельного значения x=3 можно записать

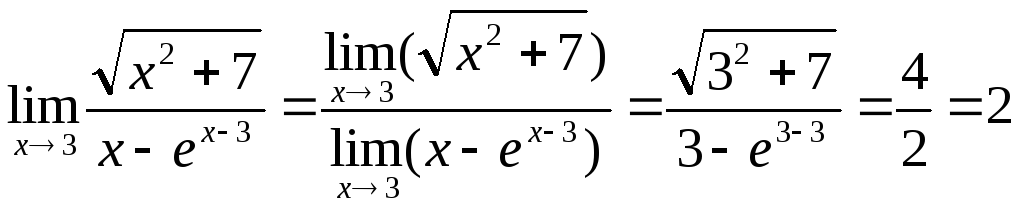
Ответ: 2

3. Найти

Решение:

При x→2 числитель дроби стремится к 0, а знаменатель к числу 10

Следовательно, применяя теоремы о пределах с последующей подстановкой предельного значения x=2 можно записать

Ответ: 0