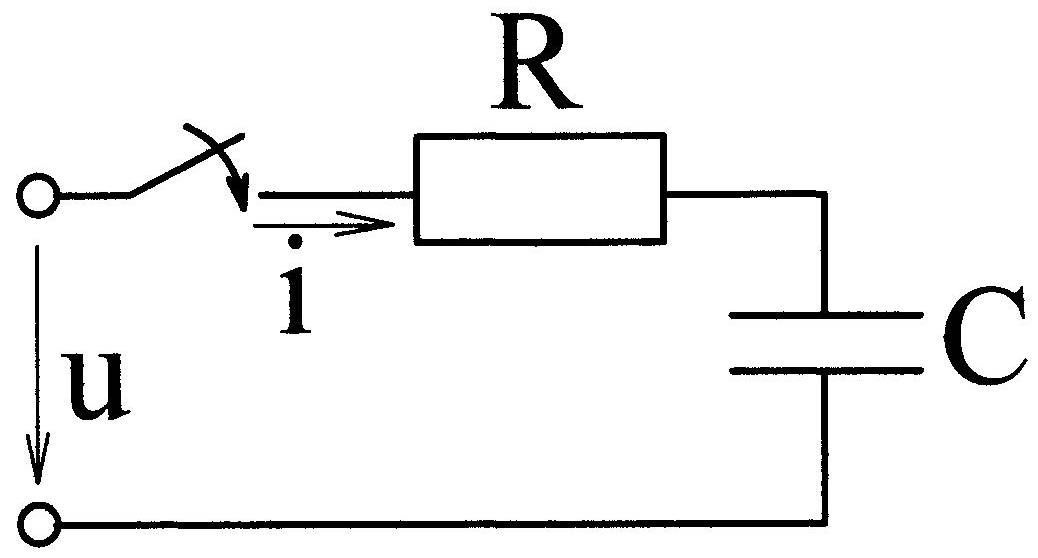
11.6.4. Включение цепи r, c на синусоидальное напряжение

Цепь R, C (рис.11.17) включается на синусоидальное напряжение

.

Начальные условия те же, что и для цепи (рис.11.15):

при , .

Дифференциальное уравнение для цепи (рис.11.17):

. (11.43)

Решение уравнения (11.43) классическим методом:

Рис. 11.17 .

Принужденную составляющую напря-

жения на емкости определим в результате расчета цепи (рис.11.17) в установившемся режиме.

Принужденный ток цепи

, (11.44)

где ; ;  0; .

Тогда принужденная составляющая напряжения на емкости будет также синусоидальна и будет отставать от тока на угол :

, (11.45)

где .

Свободная составляющая для цепи (рис.11.17) известна из (11.34):

.

Определим напряжение переходного процесса на емкости:

. (11.46)

Постоянную интегрирования A определим из начальных условий, подставив их в уравнение (11.46):

, откуда

.

Подставив A в уравнение (11.46), получим:

. (11.47)

Определим ток переходного процесса, взяв производную по времени от выражения (11.47) и умножив ее на емкость:

,(11.48)

где ; .

П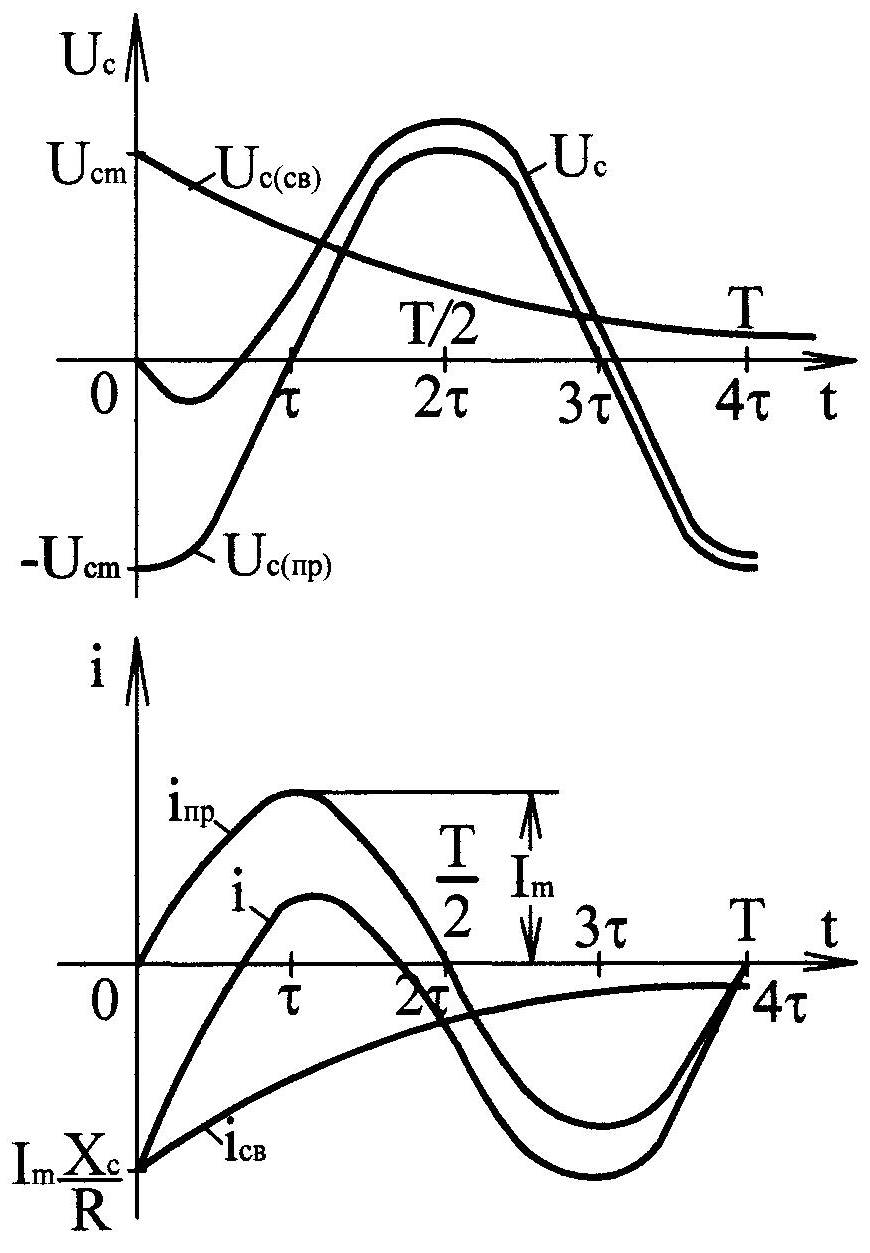 о выражениям (11.47) и (11.48) на рис.11.18 построены кривые напряжения на емкости и тока переходного процесса для цепи (рис.11.17) при . Из графика (рис.11.18) видно, что на

с инусоидальные и налагаются свободные состав-ляющие и , абсолютная величина которых уменьшается по показательному закону (экспоненте). В результате и в некоторые моменты времени превосходят и . Быстрота устано-вления режима определяется величиной постоянной времени .

Начальные значения , зависят от фазы включения , причем . Если включение

Рис. 11.18 происходит в момент, когда

должен иметь наибольшее по

абсолютной величине значение ( ), т.е. когда , то

и , и режим в цепи устанавливается сразу после включения.

Если в момент включения ( ), что будет при (рис.11.18.) и при , то начальные значения и получают по абсолютной величине наибольшие возможные значения, а именно:

и .

В последнем случае может превысить амплитуду тока в раз. Напряжение на конденсаторе в переходном режиме не может превзойти , так как наибольшее значение не может превзойти .

В качестве примера неблагоприятного переходного процесса при включении цепи R, C на синусоидальное напряжение можно привести включение ненагруженной кабельной линии под напряжение. При этом возникают большие толчки тока, для уменьшения которых включают последовательно с линией пусковые сопротивления.

11.7. Переходные процессы в цепи с последовательным соединением r, l, c

11.7.1. Короткое замыкание цепи r, l, c (разряд конденсатора на r, l)

П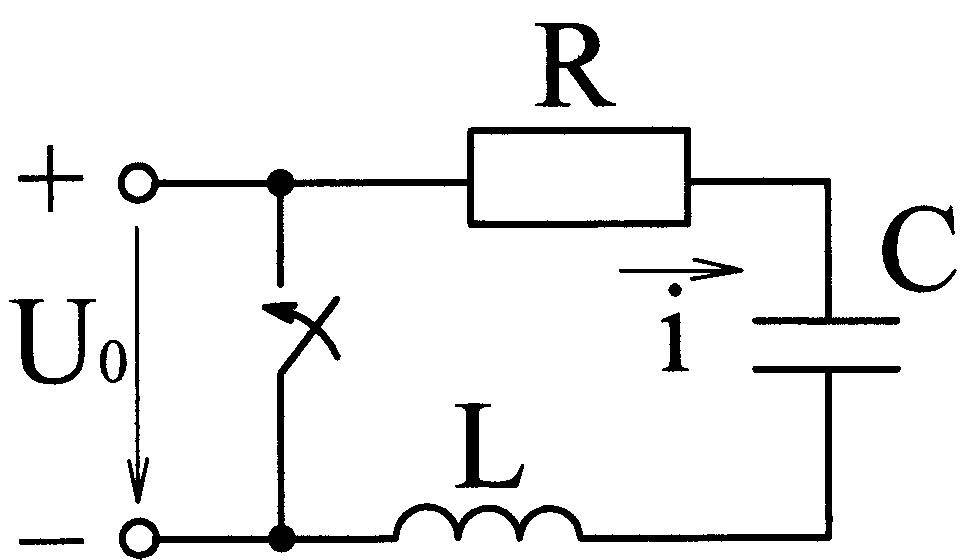 усть конденсатор С заряженный до напряжения замыкается на цепь с последовательным соединением R, L (рис.11.19). Запишем дифференциальное уравнение для цепи после коммутации:

Рис. 11.19 . (11.49)

В уравнении (11.49) два неизвестных – ток и напряжение переходного процесса. Что бы избавиться от одного из неизвестных, продифференцируем уравнение (11.49) по времени:

. (11.50)

Третье слагаемое в уравнении (11.50) умножим и разделим на емкость С и учтем, что , тогда уравнение (11.50) запишется в следующем виде:

. (11.51)

Уравнение (11.51) представляет собой однородное дифференциальное уравнение второго порядка с одним неизвестным i.

Решаем это уравнение классическим методом: ; принужденная составляющая тока , так как правая часть уравнения (11.51) равна нулю. Следовательно, .

Запишем характеристическое уравнение для дифференциального уравнения (11.51):

, или . (11.52)

Уравнение (11.52) является алгебраическим уравнением второго порядка, аналогичное уравнению из курса математики:

, корни которого

. (11.53)

В соответствии с (11.53), корнями уравнения (11.52) будут:

. (11.54)

Обозначим в уравнении (11.54):

и , (11.55)

тогда корни характеристического уравнения (11.52) примут вид:

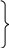
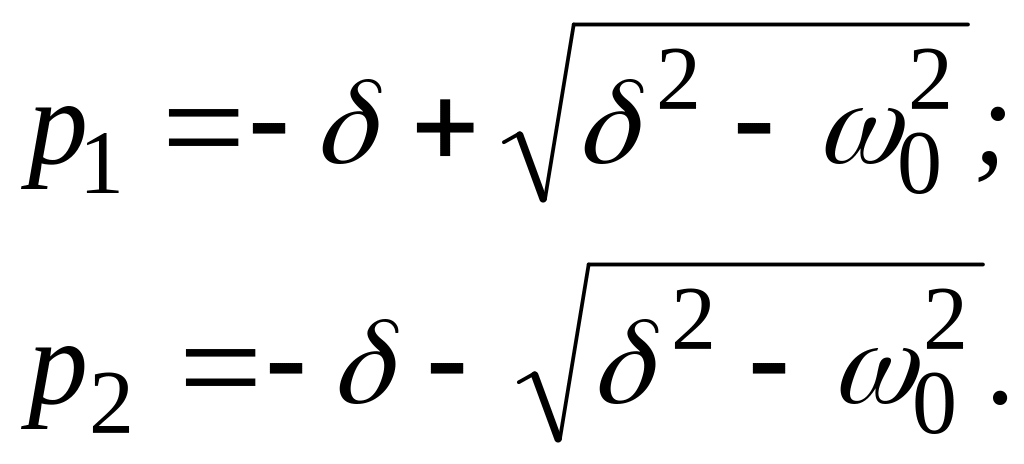(11.56)

Решение дифференциального уравнения второго порядка (11.51) должно содержать две постоянных интегрирования, для нахождения которых необходимы два начальных условия:

первое начальное условие:

, ;

второе начальное условие:

определим значение производной от тока при из уравнения (11.49):

;

подставим в это уравнение , , :

, откуда

 второе начальное условие.

Характер разряда конденсатора зависит от соотношения между R, L, C и, в конечном счете, определяется тем, будут ли корни характеристического уравнения и вещественными или комплексными.

В таблице 11.1 приведены сведения о характере разряда конденсатора на R, L в зависимости от вида корней и и общее решение однородного дифференциального уравнения второго порядка.

Таблица 11.2

Корни и	Общее решение однородного дифференциального уравнения второго порядка (11.51)	Характер разряда конденсатора на R, L
Вещественные неравные	(11.57)	Апериодический
Вещественные равные	(11.58)	Предельный апериодический
Комплексные: ;	(11.59)	Колебательный

Рассмотрим три вида разряда конденсатора на R, L.

В а р и а н т 1. Апериодический разряд конденсатора.

Предположим, что  (11.55), т.е.

 или  , (11.60)

тогда характеристическое уравнение (11.52) имеет вещественные и неравные корни . В этом случае общим решением однородного дифференциального уравнения второго порядка (11.51) будет сумма двух экспоненциальных функций (11.57). Постоянные интегрирования A₁ и A₂ находим из начальных условий. Подставляя первое начальное условие: , в уравнение (11.57), получаем: 0 = A₁ + A₂, откуда A₂ =  A₁;

. (11.61)

Возьмем производную по времени от уравнения (11.61):

. (11.62)

Подставляя в уравнение (11.62) второе начальное условие: , , получаем: , откуда, с учетом (11.56):

. (11.63)

Значение A₁ подставляем в уравнение (11.61), получаем выражение тока переходного процесса:

. (11.64)

Определим напряжения переходного процесса:

на активном сопротивлении:

;

на индуктивности:

; (11.65)

на емкости (из уравнения (11.49)):

. (11.66)

Таким образом, ток (11.64) и напряжения (11.65), (11.66) переходного процесса состоят из алгебраической суммы двух экспонент, имеющих разные знаки. Так как корни и

о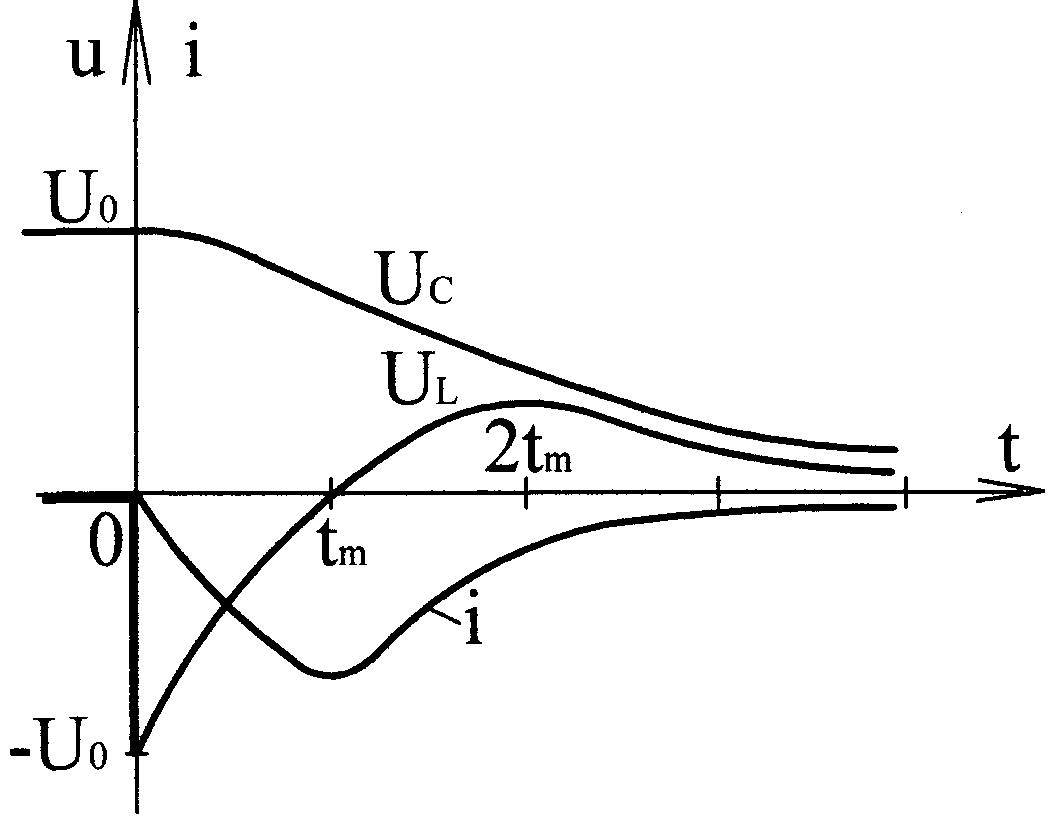 трицательны и  , то первая экспонента затухает медленнее, чем вторая. В резу-льтате, , начиная с , непрерывно убывает, оставаясь всегда положительным, так как его первая экспонента положи-тельна и больше второй отрицательной (рис.11.20). Ток , начиная с нуля, всегда отри-

Рис. 11.20 цательный, что соответствует

току разряда конденсатора.

Рассмотренный вид разряда конденсатора на R, L называется апериодическим.

Энергетическая сторона апериодического процесса заключается в следующем. Так как напряжение на конденсаторе непрерывно уменьшается, то конденсатор отдает энергию R и L. Индуктивность с увеличением тока накапливает энергию в магнитном поле, но, начиная с момента времени (рис.11.20), ток уменьшается, и индуктивность постепенно отдает энергию сопротивлению R. В течение всего процесса сопротивление R потребляет энергию, превращая ее в тепло.

В а р и а н т 2. Предельный апериодический разряд конденсатора.

В этом случае , т.к. = , тогда характеристическое уравнение (11.52) имеет вещественные и равные корни . При этом решение дифференциального уравнения (11.51) находится в виде (11.58). Постоянные интегрирования A₃ и A₄ находим из начальных условий. Подставляя первое начальное условие: , в уравнение (11.58), получаем: A₃ = 0, тогда

. (11.67)

Возьмем производную по времени от уравнения (11.67):

. (11.68)

Подставляя в уравнение (11.68) второе начальное условие: , , получаем: .

Из уравнения (11.67) имеем:

. (11.69)

Напряжения переходного процесса на индуктивности и на емкости:

; (11.70)

. (11.71)

Рассматривая выражения (11.69) - (11.71) для тока и напряжений переходного процесса, мы придем к таким же заключениям, что и при  . Таким образом, при мы имеем предельный случай апериодического разряда конденсатора. При дальнейшем уменьшении R, разряд из апериодического переходит в колебательный.

В а р и а н т 3. Колебательный разряд конденсатора.

В этом случае  т.к.  , характеристическое уравнение (11.52) в этом случае имеет комплексные корни.

Обозначим , тогда:

(11.72)

Общее решение однородного дифференциального уравнения (11.51) в этом случае имеет вид (11.59). Постоянные интегрирования A₅ и A₆ находим из начальных условий. Подставляя первое начальное условие: , в уравнение (11.59), получаем: A₆ = 0, тогда

. (11.73)

Определим производную по времени от уравнения (11.73):

. (11.74)

Подставляя в уравнение (11.74) второе начальное условие: , , получаем: , .

Подставляя значение A₅ в уравнение (11.73), имеем:

. (11.75)

Обозначив , получим

. (11.76)

Напряжения переходного процесса:

; (11.77)

. (11.78)

Построим по выражению (11.76) кривую тока переходного процесса (рис.11.21).

К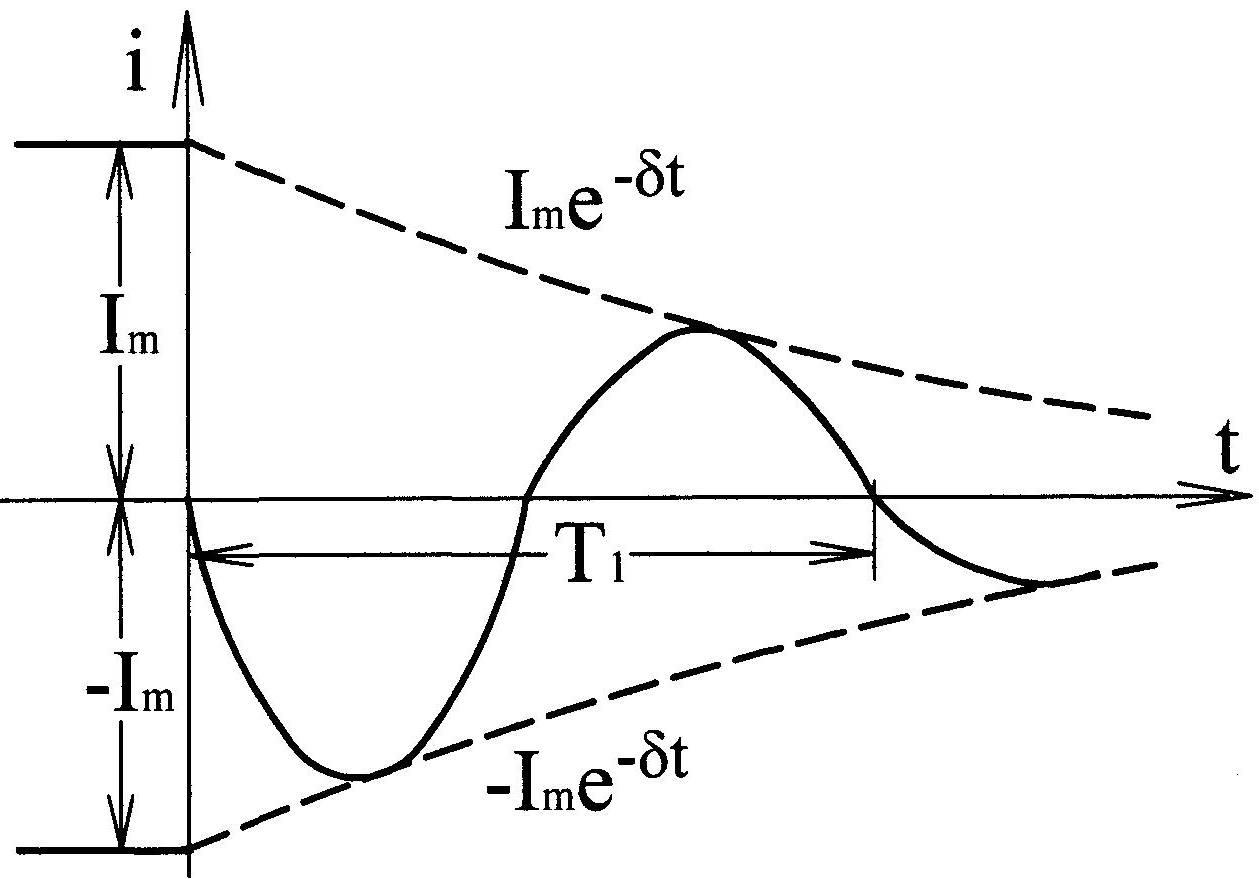 ак видно из выражений (11.76)-(11.78) для тока и напряжений переходного процесса и графика (рис.11.21), разряд конден-сатора на R, L носит колеба-тельный характер, причем амплитуды тока и напря-жений постепенно уменьша-ются, так как множитель

Рис.11.21 с ростом времени t

стремиться к нулю. Угловая

частота этих собственных затухающих колебаний

меньше угловой частоты собственных незатухающих колебаний , а период затухающих колебаний больше периода незатухающих колебаний:

 .

Для предельного случая сверхпроводящей цепи, когда , имеем:

, ; (11.79)

Следовательно, если бы в цепи не происходило рассеяние энергии, ток и напряжения были бы синусоидальными функциями времени, т.е. имели бы место так называемые собственные незатухающие колебания, угловая частота которых равна резонансной частоте этой цепи .