
- •Теории управления квантовыми системами.
- •Содержание
- •Введение
- •1. Основные понятия и определения квантовой механики
- •1.1. Чистые и смешанные состояния
- •1. 2. Обозначения Дирака
- •1. 3. Перепутанные состояния
- •2. Элементы квантовой теории информации
- •2. 1. Кубиты
- •2. 2. О квантовой информации
- •2. 3. Преобразование одного кубита
- •2. 4. Перепутывание
- •2.5. Перепутывание и квантовая неразличимость
- •2.6. Логический элемент «управляемое не»
- •3. Парадокс эйнштейна – подольского – розена (эпр)
- •4. Неравенства белла
- •5. Квантовая криптография
- •5.1. Понятие о криптографии
- •5.2. Ключи и их распределение
- •5.3. Открытые ключи
- •5.4 Понятие о квантовой криптографии
- •5.4.1. Защита посредством неортогональных состояний
- •5.4.2. Защита посредством перепутывания
- •5.4.3. Практическая реализация квантово – криптографических систем
- •6. Квантовая телепортация
- •6.1 Общие представления
- •6.2. Протокол квантовой телепортации
- •6. 3. Обзор некоторых экспериментальных результатов по квантовой телепортации
- •6.4. Заключительные замечания: возможна ли телепортация макрообъекта?
- •7. Квантовые вычисления. Квантовые компьютеры.
- •7.1. Вводные замечания
- •7.2. Квантовый регистр
- •7.3. Задачи поиска.
- •7.4. Квантовые алгоритмы
- •7.4.1. Моделирование времени.
- •7.4.2. Моделирование вероятности
- •7.4.3. Алгоритм разложения на простые множители или алгоритм Шора
- •7.5. Общие требования к квантовым компьютерам Практическая реализация
- •Приложение. Гипотезы о квантовой природе сознания
- •Заключение
- •Словарь терминов
- •Литература
2. 3. Преобразование одного кубита
Одно из основных преобразований в квантовой теории информации – это преобразование Адамара. Оно действует на кубит следующим образом:
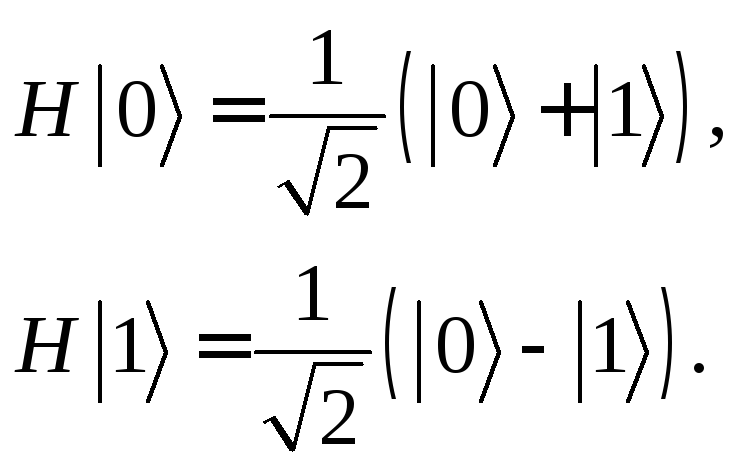
Применив, например, его к кубиту
|![]()
получим
![]()
т.е. строго определённое значение кубита. Это было бы невозможно сделать с некогерентной смесью.
Рассмотрим действие простого делителя, делящего луч в отношении50/50. Такие делители были реализованы не только для фотонов. Пусть имеется две входящие и две выходящие моды.
вход
выход
|0>in
|0>out
1
H
3


2
4
|1>in
|1>out
Рис. 2.3. Действие простого делителя
Частица, падающая
сверху или снизу на такой делитель,
появится либо в верхнем, либо в нижнем
выходящем луче с одной и той же вероятностью
0,5.
Д
![]() ,
,
Фазовое действие делителя будет описываться преобразованием Адамара.
Предположим, что состояние на входе – произвольный кубит
![]()
Для одной частицы
это означает, что
![]() -это
амплитуда вероятности обнаружить
частицу, падающую на делитель сверху,
а
-это
амплитуда вероятности обнаружить
частицу, падающую на делитель сверху,
а![]() - амплитуда обнаружить частицу, падающую
снизу. Тогда в результате действия
делителя, получается конечное состояние
- амплитуда обнаружить частицу, падающую
снизу. Тогда в результате действия
делителя, получается конечное состояние
![]() ,
,
так что амплитуда
вероятности найти частицу в верхнем
выходящем пучке равна
![]() ,
а амплитуда вероятности найти её в
нижнем пучке равна
,
а амплитуда вероятности найти её в
нижнем пучке равна![]() .
В частности, если
.
В частности, если![]()
или
![]() =0,
то частицу с равной вероятностью можно
обнаружить в любом из выходящих пучков.
В случае же
=0,
то частицу с равной вероятностью можно
обнаружить в любом из выходящих пучков.
В случае же![]() частица будет обязательно обнаружена
в верхнем пучке и никогда не будет
обнаружена в нижнем пучке.
частица будет обязательно обнаружена
в верхнем пучке и никогда не будет
обнаружена в нижнем пучке.
Рассмотрим последовательность таких делителей, осуществляющих последовательность преобразований Адамара. Используется интерферометр Маха-Цандера с двумя одинаковыми делителями
|0>out

|0>in




|1>in
|1>out
З2
Н Н



Рис. 2.4. Действие последовательности делителей и двух преобразований Адамара
В данном случае зеркала нужны только для того, чтобы перенаправить пучки. Действие интерферометра как последовательность двух последовательных преобразований Адамара представляется в виде:
![]()
Результат прямо следует из того факта, что двойное действие преобразования Адамара есть тождественное преобразование - на выходе интерферометра воспроизводится входное состояние. В частном случае, когда на входе имеется только одно состояние ( = 1, = 0), на выходе частица будет обнаружена в верхнем пучке, хоть и внутри интерферометра эта частица имеет одинаковые вероятности оказаться в каждом из плеч. Дело в том, что выходные амплитуды вероятностей определяются относительной фазой, набегающей в интерферометре. В оптике этот эффект изучен досконально и не вызывает удивления. С массивными частицами, поведение которых можно описывать волнами де Бройля дело происходит точно также.
На языке теории квантовой информации рассмотренный эффект формулируется так: кубит на выходе интерферометра имеет определенное значение, если и только если кубит на входе имеет определенное значение, внутри интерферометра его состояние максимально неопределенно.
Кроме элемента Адамара важным квантовым логическим элементом является фазовращатель Ф. Его действие состоит в том, чтобы вносить сдвиг фаз у одного из пучков (будем считать, что это происходит в нижнем пучке, хотя это не важно - важна только относительная фаза).
|0>in
|0>out
З1




ei

|1>in
|1>out
З2
Н Н
Ф



Рис. 2.5. Действие последовательности делителей и фазовращателя
Действие фазовращателя можно описать унитарным преобразованием
![]() ,
,
![]()
Значит, выходной кубит можно вычислить, применяя последовательно все соответствующие преобразования к кубиту, который был на входе
![]() .
.
Если на входе
имеется только один пучок, например,
![]() ,
т.е.
,
т.е.![]() =0.
Тогда конечное состояние будет
=0.
Тогда конечное состояние будет
![]()
Для
![]() значение кубита определено и равно «0».
Для
значение кубита определено и равно «0».
Для![]() значение кубита равно «1». Таким образом,
фазовый сдвиг может переключать состояние
выходного кубита между «0» и «1». В общем
случае произвольного сдвига вероятность
того, что кубит имеет значение «0» будет
значение кубита равно «1». Таким образом,
фазовый сдвиг может переключать состояние
выходного кубита между «0» и «1». В общем
случае произвольного сдвига вероятность
того, что кубит имеет значение «0» будет![]() ,
а вероятность того, что кубит имеет
значение «1», будет
,
а вероятность того, что кубит имеет
значение «1», будет![]() .
.
