1. 2. Обозначения Дирака

Для изображения квантового состояния в формализме Шредингера используется волновая функция - функция совокупности координатв определённый момент времени t, символ a – индекс состояния, набор соответствующих квантовых чисел, которые определяют состояние. Например, для атома водорода -, n, m, l-квантовые числа, определяющие состояние электрона, r,,-пространственные координаты электрона.

Скобочное обозначение Дирака для состояния имеет вид <|a>, т.е. =<|a>. Состояние a квантовой системы описывается вектором состояния «кет» |a> или вектором состояния “бра» <|a. Эти векторы связаны между собой: <|a=|a>. Эрмитовы операторыдействуют на кет-вектор слева, а на бра-вектор – справа и преобразуют их в другие векторы состояний, соответственно, - кет или бра. Например, если |b>=, то <b|=(=<a|=<a|. Скалярное произведение <, матричный элемент оператора

1. 3. Перепутанные состояния

Впервые понятие «перепутанных» или "сцепленных" состояний было введено Э.Шредингером в 1935г. Шредингер ввел понятие перепутанных состояний для описания состояния совокупной или составной системы, которая состоит из нескольких частей, причем части общей системы могут быть пространственно разнесены. Шрёдингер назвал свойство сцепленности "…самой главной характерной особенностью квантовой механики, которая заставляет полностью отказаться от классических представлений". Сцепленные объекты связаны между собой на любом расстоянии. Квантовая запутанность — это не теоретическая абстракция, которую ввели физики-теоретики, а объективный факт окружающей реальности. Это то, что существует в природе независимо от наших представлений, собственно, поэтому она и может быть использована на практике.

Квантовая запутанность возникает в системе, состоящей из двух и более взаимодействующих подсистем (или взаимодействовавших ранее, а затем разделенных), и представляет собой суперпозицию различимых состояний. В таких системах флуктуации отдельных частей взаимосвязаны, но не посредством обычных классических взаимодействий, а посредством нелокальных квантовых корреляций. В этом случае изменение одной части системы в тот же момент времени сказывается на остальных ее частях (даже если они разделены в пространстве). В настоящее время свойства запутанных состояний подтверждены многочисленными физическими экспериментами, и именно эти возможности лежат в основе работы квантового компьютера, когда все кубиты, благодаря квантовой запутанности, могут согласованно и мгновенно изменять свое состояние, даже если изменяется состояние одного кубита.

Запутанность — это особый тип взаимосвязи между составными частями системы, у которой нет аналога в классической физике. Квантовая запутанность — состояние неразрывной целостности, единства. Запутанное состояние — это состояние составной системы, которую нельзя разделить на отдельные, полностью самостоятельные и независимые части. Оно является несепарабельным (неразделимым). Запутанность и несепарабельность — тождественные понятия.

По принципу сепарабельности состояния любых сепарабельных (отделимых) по пространству и времени подсистем S₁, S₂, ..., S_N составной системы S индивидуально хорошо определены, так же и состояния составной системы целиком и полностью определены ее подсистемами и их физическими взаимодействиями, включая их пространственно-временные отношения.

Рассмотрим эксперимент, проведённый в Рочестерском университете Л. Манделом с сотрудниками в начале 90-х годов 20 века.

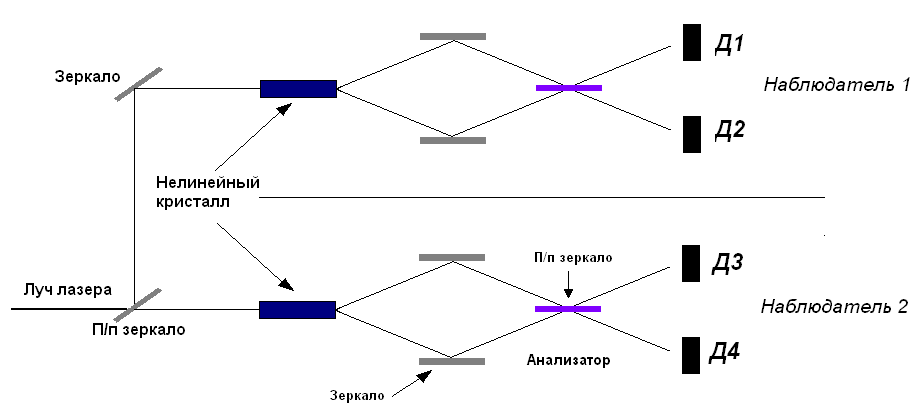
Рис. 1.1. Схема эксперимента по перепутанным состояниям фотонов.

Лазерный луч с помощью полупрозрачного зеркала расщеплялся на два пучка, а затем каждый из пучков направлялся на так называемый нелинейный кристалл, способный расщеплять квант света (фотон) на два дочерних кванта. Закон сохранения энергии при этом, конечно же, выполняется: энергия каждого из дочерних квантов вдвое меньше энергии материнского кванта. Например, если падает луч лазера с длиной волны 405 нм (синего цвета), то на выходе из кристалла будут два луча с длиной волны 810 нм (красного цвета), энергия каждого кванта которых вдвое меньше энергии кванта в исходном луче. Затем с помощью системы зеркал делалось так, что каждая из этих двух пар фотонов интерферировала между собой. Результаты наблюдения интерференционной картины фиксировались детекторами Д1-Д2 для первой пары фотонов и детекторами Д3-Д4 - для второй пары.

Как известно, любая частица, обладающая ненулевым спином, в том числе фотон, характеризуется поляризацией, то есть проекцией спина на направление движения. Фотоны могут обладать двумя состояниями поляризации, отвечающими двум возможным проекциям спина - вдоль и против направления движения. Вид поляризации света определяет плоскость колебаний электрического поля электромагнитных волн, и существуют так называемые анализаторы (специальные кристаллы), способные пропускать кванты только с определённой поляризацией. Поскольку различные состояния поляризации находятся в состоянии суперпозиции, то с помощью такого кристалла можно выделять те или иные её компоненты. Если подобный кристалл поставить по ходу одного из лучей и вращать его относительно оси луча, то интерференционная картина будет меняться из-за изменения соотношения между компонентами суперпозиции. Подобные действия в данном эксперименте приведут к изменению вероятностей регистрации фотонов (одного или двух) каждым из детекторов. Итак, были пространственно разнёсены два пучка на достаточно большое расстояние и менялись с помощью анализатора соотношения между компонентами суперпозиции на одном из них (нижнем на рис. 1.1). В силу таких манипуляций интерференционная картина на этом пучке менялась. На втором пучке никаких манипуляций не производилось. Но интерференционная картина, наблюдаемая на этом втором пучке, точно повторяла интерференционную картину на пучке, с которым экспериментировал Мандел. И картина эта менялась мгновенно, в то же самое время, когда менялась картина на первом пучке. Экспериментатор в этом случае никак не взаимодействовал с объектом наблюдения, и никакого материального носителя взаимодействия между пучками не было. Выходит, квантовый объект каким-то образом узнавал, что происходит с другим объектом, удалённым от него на значительное расстояние (сейчас проведены эксперименты с расстоянием между парами фотонов более 100 км).    Подобную связь между частицами называют квантовыми корреляциями, а состояния участвующих в них частиц запутанными. Запутанные или сцеплённые состояния в общем случае могут возникать в системе, которая в какой-то момент времени распадается на невзаимодействующие подсистемы. Например, если электрон сталкивается с атомом, то образуется запутанное состояние, в котором состояние электрона будет коррелированно с состоянием атома в результате произошедшего взаимодействия. Отметим, что запутанное состояние не может быть представлено в виде совокупности состояний отдельных частей системы в силу наличия корреляций между ними. Также, запутанность - это физическая величина, которая имеет количественные характеристики, и она может быть определена непосредственно в эксперименте.   Суперпозиционные состояния - более общее понятие, чем запутанные состояния. В них компоненты волновой функции могут быть как коррелированны между собой, так и нет. Последний случай отвечает наличию в системе изолированных подсистем, которые никогда не взаимодействовали друг с другом. В эксперименте Мандела запутанные состояния пар фотонов возникали в ходе расщепления исходного кванта на нелинейном кристалле, а лазер был необходим для создания совершенно идентичных по своим характеристикам фотонов.

Теперь представим, что возле одного из пучков находится Наблюдатель 2 (Н 2), который проводит эксперименты, а возле другого – Наблюдатель 1 (Н 1), который не знает о существовании Н 2. Для Н 1 изменение результатов эксперимента на его пучке выглядит как чудо. Ведь Н 1 ничего не делает со своим пучком, все условия эксперимента остаются постоянными, а интерференционная картина по совершенно, казалось бы, непонятным причинам меняется. Похожую схему можно использовать и для "мгновенной" передачи информации между Н 1 и Н 2. Посредством присоединения третьей - "информационной" - частицы к одной из сцепленных частиц у Н 2 можно передать ее свойства другой подобной частице, находящейся на установке Н 1. То есть мы можем не только мгновенно передать информацию о состоянии какой-либо частицы, но и воспроизвести это состояние. И закодировать в последовательности передаваемых состояний любое сообщение.   Явление мгновенной передачи свойств частицы на расстояние получило название квантовой телепортации (см. далее). Способ практической реализации этого эффекта был предложен в 1993 году группой Чарльза Беннета (IBM), а само явление впервые наблюдалось в работах австрийских исследователей из университета в Инсбруке, возглавляемых Антоном Цайлингером, и итальянских, из Римского университета под руководством Франческо Де Мартини в 2001 - 2002 годах. Однако для передачи информации необходимо, чтобы Н 1 и Н 2 согласовали свои действия. Ведь по поступающим сигналам нельзя определить, передаёт ли коллега сообщение, или нет. Поэтому нужно либо заранее договорится о времени передачи, либо об условном сигнале (например, определённой последовательности переданных состояний), означающим начало передачи. И, конечно, необходимо договориться о кодировке сообщений, - то есть, какая последовательность состояний означает, к примеру, ту или иную букву алфавита. Вообще говоря, никакой "передачи" информации не происходит, информация просто распределена между подсистемами, а Н 1 и Н 2 в ходе подобного эксперимента имеют доступ к единому нелокальному объекту. Для мгновенного обмена информацией необходимо сначала где-то создать запутанные пары фотонов и как-то переслать им. На сегодняшний день, использование оптоволоконных технологий позволяет сохранить запутанность пар фотонов на расстояниях до нескольких сотен километров, это пока создаёт предел для реализации устройств мгновенной квантовой связи. Но это чисто технический вопрос, рано или поздно он будет решён, и уже сейчас интенсивно обсуждаются вопросы создания глобальных систем квантовой связи. Можно высказать предположение и о создании "квантовых консервов" - устройств, в которых когерентность состояний тех или иных объектов не разрушается достаточно долго, и которые можно будет просто брать с собой. Не противоречит ли возможность мгновенной передачи информации теории относительности? Нет, не противоречит. Теория относительности говорит о пределе в виде скорости света на скорость движения материальных объектов и скорость передачи взаимодействия между ними. Это совершенно справедливо для локальных (классических) объектов. В случае же пар фотонов в запутанном состоянии нет никакого взаимодействия между ними, нет никакой передачи информации между ними, они просто остаются единым объектом, как бы далеко друг от друга не находились. Это грань реальности, которая выходит за рамки теории относительности. Предположим, что Н 2 находится возле нас, а Н 1, вместе со своей установкой и источником пар фотонов - возле звезды, расстояние до которой миллион световых лет. То есть Н 1 поставил свои эксперименты миллион лет назад, а до Н 2 только сейчас долетел свет из расщеплённого пучка, и он начал свои манипуляции с ним. Что же будет? Результат не изменится: проводимые сейчас эксперименты Н 2 изменят результаты экспериментов Н 1, который, может быть, уже давным-давно умер, и даже успел опубликовать их результаты. Ведь определение Н 2 состояния фотонов определяет свойства фотонов Н 1, и результаты у того меняются вне зависимости от расстояния между ними и прошедшего времени. То есть более позднее во времени действие влияет на произошедшее ранее событие. Это парадокс, неразрешимый в рамках классического подхода, в квантовой механике следует понимать так, что физическая интерпретация более ранних экспериментов зависит от позднейших измерений. Если же Н 1 не знает о проводимом Н 2 эксперименте, он вероятнее всего решит, что необъяснимые статистически результаты эксперимента вызваны какими-либо неполадками в установке. Он ведь не может найти никаких причин для аномальных результатов, поскольку они находятся в другом событийном пространстве.   Подобный эффект обратной причинности был совсем недавно исследован группой Антона Цайлингера. Предсказания квантовой механики подтвердились в очередной раз: более ранняя регистрация фотонов Н 1 по сравнению с действиями Н 2 никак не сказывается на результатах эксперимента.

Настоящая квантовая теория начинается там, где появляются несепарабельные состояния. Причем речь идет не о каких-то «интерпретациях», в которых эта несепарабельность (квантовая запутанность) вводится с некой «хитрой» целью, а о стандартной квантовой теории, и наличие несепарабельных состояний — это естественное следствие основного принципа квантовой механики — принципа суперпозиции состояний.

Т.о., несепарабельные состояния отдельной системы никакими ухищрениями типа статистической (ансамблевой) интерпретации невозможно свести к привычным классическим представлениям и сепарабельным состояниям.

В квантовой теории известен принцип несепарабельности: если две системы взаимодействовали в прошлом, то в общем случае невозможно приписать один вектор состояния любой из двух подсистем.

Этот принцип является прямым следствием общих правил квантовой механики. Принцип является всеобщим, и взаимодействия могут быть любого рода, между любыми системами.

Принцип несепарабельности — самый общий, и обычно мы имеем дело с целым набором самых различных взаимодействий с окружением, при этом отдельным взаимодействиям соответствует своя степень квантовой запутанности (несепарабельности). Вот почему в «игру» вступают относительные величины квантовой запутанности. Для сильных классических взаимодействий сепарабельность выше, поэтому хорошо работает приближение, не принимающее во внимание квантовую запутанность в классической физике. Однако подсистемы могут находиться в практически сепарабельном состоянии по одним степеням свободы, но несепарабельны по другим. Например, мы сепарабельны (разделены) в своих физических телах, но в какой-то мере несепарабельны по чувствам и еще более — по мыслям.

В настоящее время под «квантовой системой» в общем случае понимается любая система, описываемая в терминах состояний, то есть посредством «вектора состояния», «матрицы плотности» и т. д. Это наиболее полное описание. А классическая физика для макросистем — лишь частный случай квантового описания, предельный случай, когда мы пренебрегаем несепарабельностью. Вся классическая физика — это сепарабельное описание.

Макросистемы отличаются от микрочастиц только в одном плане — на микроуровне эффекты несепарабельности выражены наиболее явно, для микрочастиц квантовые корреляции сравнимы с классическими взаимодействиями, поэтому без запутанности тут уже не обойтись.

«Вычеркнуть» запутанность очень просто — достаточно ею пренебречь и не принимать во внимание.

Несепарабельные (запутанные) состояния не имеют никакого аналога в классической физике. Они никак не могут быть ею объяснены и описаны. Вообще же чистых сепарабельных состояний вокруг нас нет — все когда-то образовалось, вероятно, из единого источника, однако методами квантовой теории можно описывать неотделимые состояния как отделимые, пренебрегая запутанностью, обнуляя недиагональные элементы в матрице плотности. Так и получается классическая физика.

Полная несепарабельность — это максимальная запутанность с окружением по всем степеням свободы, что означает полную нелокальность объекта. Если объекты локализованы, значит, по каким-то степеням свободы мы можем записать сепарабельный вектор состояния (диагональную матрицу плотности), взяв в качестве базисных векторов сепарабельные собственные состояния. Например, запутанную по спинам пару частиц можно описать двумя различными векторами состояния: один вектор — в координатном представлении — тогда частицы будут сепарабельны по координатам, и с каждой частицей сопоставляется свой вектор состояния (тоже в координатном базисе). С другой стороны, мы можем записать вектор состояния этой пары частиц в спиновом представлении, в базисе по спиновым степеням свободы. Тогда система будет несепарабельна по этим степеням свободы, и мы уже не сможем записать свои векторы состояния для каждой частицы в этом базисе.

Когда квантовая теория обогатилась пониманием того, что квантовая запутанность — это обычная физическая величина, и с ней можно работать, как с другими физическими величинами, такими как энергия, масса и т. д., то возникла необходимость в ее количественном описании. Запутанные состояния нужно было охарактеризовать по величине (степени) запутанности. Одним из первых такую количественную характеристику, то есть меру запутанности, ввел в 1996 году Чарльз Беннетт с соавторами.

В зависимости от величины квантовой запутанности (она изменяется от нуля до единицы) система может состоять из отделимых локальных частей, которые слабо связаны друг с другом. В этом случае мера запутанности близка к нулю. Если же система составляет единое неразделимое целое, то мера запутанности равна единице. Это нелокальное состояние, и тогда в системе нет никаких классических, «видимых» объектов.

Разделить на строго независимые части можно систему, части которой находятся в сепарабельном (незапутанном) состоянии (мера запутанности равна нулю). Такое разделение возможно только в том случае, если части системы никогда не взаимодействовали друг с другом.

Вообще любой объект, который взаимодействует со своим окружением, находится с ним в запутанном состоянии. Величина запутанности зависит от интенсивности взаимодействия. Так, управляя взаимодействием с окружением, можно манипулировать мерой квантовой запутанности между составными частями системы. Например, замкнутая система может находиться в максимально запутанном состоянии и не будет иметь внутри себя локальных (классических) составных частей (подсистем). Но если она начинает взаимодействовать с окружением, то мера запутанности между ее подсистемами постепенно уменьшается, и они «проявляются» в виде локальных объектов. При наличии взаимодействия с окружением суперпозиция разрушается, и проявляется то или иное локальное состояние в зависимости от типа взаимодействий. Этот физический процесс называется декогеренцией. Догеренция – это процесс перехода чистого состояния в смешанное. Другой стороной этого процесса является возрастание меры запутанности системы с окружением. Оно будто «растаскивает» в разные стороны части того, что раньше было единым целым, придает им определенную форму, и они становятся видимыми, различимыми с нашей привычной, классической точки зрения.

Именно процесс догеренции создает много сложностей при разработке квантового компьютера, поскольку нарушает когерентную согласованную работу кубитов. Вследствие декогеренции вместо внутренней запутанности между кубитами, которой компьютер может управлять и которая полностью ему подвластна, возникает запутанность с окружением. Работать с ней квантовый компьютер не в состоянии

Существует и обратный процесс - запутанность можно «концентрировать», увеличивать. Этот процесс называется рекогеренцией.

Декогеренция и рекогеренция — самые фундаментальные физические процессы в окружающей реальности, известные науке к настоящему времени. Процесс декогеренции лежит в основе всех известных классических взаимодействий (гравитационного, электромагнитного и т. д.), которые можно считать лишь его следствием. Различные виды взаимодействий в этом плане рассматриваются как отдельные каналы декогеренции. Взаимодействия могут быть любые — все, которые сопровождаются изменением состояния системы.

В физических экспериментах можно изучать различные типы взаимодействий непосредственно в аспекте декогеренции. Это, например, делалось в экспериментах А. Цайлингера (Nature 427, 711–714 (2004), где исследовался процесс декогеренции по одному из каналов взаимодействия с окружением — за счет теплового излучения. Эти процессы фундаментальные, и характерны они не только для микрочастиц, а для любых объектов, в том числе и для макроскопических тел. Декогеренция тепловым излучением — общий механизм, который относится ко всем макроскопическим телам. По большому счету, все взаимодействия являются «эффектом декогеренции». Более того, согласно теории декогеренции, весь классический мир — это «эффект декогеренции».

Мера квантовой запутанности непосредственно связана с информацией, содержащейся в системе, которая может быть выражена количественно, например, через энтропию фон Неймана для чистых состояний.

Проиллюстрируем на простом примере процесс "приготовления" запутанных состояний, рис. 1.2. Рассмотрим источник, испускающий пары частиц так, что одна из них 1 летит налево, а другая 2 - направо. Потребуем, чтобы сохранялась сумма импульсов частиц. Введем дополнительную параметризацию. Каждая частица может полететь и вверх - состояние , и вниз – состояние). Т.к. сумма импульсов сохраняется, то, если первая частица полетела налево вниз, то вторая полетит направо вверх или наоборот, - если первая частица полетела налево вверх, то вторая вынуждена полететь направо вниз.

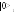
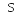
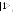
Рис. 1.2. Иллюстрация «приготовления» перепутанных состояний

Полное состояние, которое «приготавливает» источник, записывается в виде суперпозиции двух “возможностей”:

(1.1)

Коэффициенты с_i (i = 1, 2) - это (комплексные) амплитуды двух исходов. Физический смысл состоит в том, что соответствующие квадраты модулей определяют вероятности обнаружить пару частиц в состояниях(первая – вверх, вторая – вниз), либо(вторая – вверх, первая – вниз). Состояние (1.1) -пример перепутанного состояния двух частиц Другие примеры - ионы в ловушках, ядерные спины в молекуле при электронном парамагнитном резонансе, состояния системы «атом-поле» в резонаторе и др.

Перепутанными считаются состояния составной системы, которые не могут быть представлены в виде произведения волновых функций, описывающих ее части по отдельности.

Перепутанные состояния характеризуются следующими атрибутами:

• наличие параметра, принимающего ряд фиксированных значений для каждой из подсистем;

• наличие корреляций между двумя подсистемами по этому параметру, или в более общем случае - синхронности флуктуаций этого параметра;

Другое определение перепутанных состояний для двух подсистем: перепутанными называются две подсистемы, между которыми существуют квантовые корреляции по параметру, принимающему, по крайней мере, два значения для каждой из подсистем. Измерение состояния одной из подсистем однозначно определяет (проецирует) состояние другой. Совместное состояние двух подсистем тогда называется перепутанным. Корреляции должны носить квантовый характер, т.е. их нельзя описать классически. В противном (классическом) случае даже полные (т.е. 100%-ые) корреляции не дают результатов, к которым ведет использование истинных перепутанных состояний.