
- •Теории управления квантовыми системами.
- •Содержание
- •Введение
- •1. Основные понятия и определения квантовой механики
- •1.1. Чистые и смешанные состояния
- •1. 2. Обозначения Дирака
- •1. 3. Перепутанные состояния
- •2. Элементы квантовой теории информации
- •2. 1. Кубиты
- •2. 2. О квантовой информации
- •2. 3. Преобразование одного кубита
- •2. 4. Перепутывание
- •2.5. Перепутывание и квантовая неразличимость
- •2.6. Логический элемент «управляемое не»
- •3. Парадокс эйнштейна – подольского – розена (эпр)
- •4. Неравенства белла
- •5. Квантовая криптография
- •5.1. Понятие о криптографии
- •5.2. Ключи и их распределение
- •5.3. Открытые ключи
- •5.4 Понятие о квантовой криптографии
- •5.4.1. Защита посредством неортогональных состояний
- •5.4.2. Защита посредством перепутывания
- •5.4.3. Практическая реализация квантово – криптографических систем
- •6. Квантовая телепортация
- •6.1 Общие представления
- •6.2. Протокол квантовой телепортации
- •6. 3. Обзор некоторых экспериментальных результатов по квантовой телепортации
- •6.4. Заключительные замечания: возможна ли телепортация макрообъекта?
- •7. Квантовые вычисления. Квантовые компьютеры.
- •7.1. Вводные замечания
- •7.2. Квантовый регистр
- •7.3. Задачи поиска.
- •7.4. Квантовые алгоритмы
- •7.4.1. Моделирование времени.
- •7.4.2. Моделирование вероятности
- •7.4.3. Алгоритм разложения на простые множители или алгоритм Шора
- •7.5. Общие требования к квантовым компьютерам Практическая реализация
- •Приложение. Гипотезы о квантовой природе сознания
- •Заключение
- •Словарь терминов
- •Литература
7.4. Квантовые алгоритмы
Говоря о квантовых алгоритмах, как о наборе вычислительных процедур, основанных на законах квантовой механики, в первую очередь принципиален вопрос об обоснованности таких вычислений вообще. Впервые, по-видимому, это было сделано Ричардом Фейнманом в начале 80-ых годов. Вопрос, который он ставил, звучал приблизительно так: как построить гамильтониан физической системы, которую можно рассматривать в качестве компьютера?
Прежде чем ответить на этот вопрос, рассмотрим сами предпосылки обращения к квантовой механике как к теории, способной дать новые вычислительные алгоритмы. О каком же компьютере идет речь, когда говорят о моделировании законов физики? В науке о вычислениях обычно не рассматривается вопрос о конкретном вычислительном устройстве - речь идет об универсальном компьютере. Поэтому вопрос перефразируется так - могут ли законы физики быть смоделированы при помощи универсального компьютера? Будем считать, что элементы такого компьютера локально соединены между собой, но пусть это не будет бесконечно большое число соединений. Какого рода физические законы мы хотим моделировать на этом компьютере? Прежде всего - законы в классическом приближении, когда работают локальные дифференциальные уравнения. Но реальный мир - это квантовый мир, поэтому хотелось бы симулировать квантовую физику. Что же за симуляции мы будем рассматривать? Это, конечно, аппроксимационное моделирование, в котором строятся численные алгоритмы решения дифференциальных уравнений. Затем компьютер производит вычисления на основе этих алгоритмов, и мы получаем примерное представление о том, как работает физика. Это законный подход, но речь пойдет о другом. Хочется говорить о том, насколько возможно точное моделирование, т.е. так как это происходит на самом деле в природе. Если существование такой возможности было бы доказано и такой тип компьютера стал бы реальностью, то оказалось бы, что все, что происходит в ограниченном объеме пространства и времени точно бы анализировалось за ограниченное число логических операций. Очевидно, что существующие физические теории не позволяют сделать это. В противном случае мы бы работали с бесконечно малыми элементами пространства, бесконечно большими длинами волн, суммировались бесконечные ряды и т.д., т.е. если бы такое предположение было бы верным, то законы физики не работали.
Но теперь мы имеем представление о том, как модифицировать законы физики. Например, мы должны изменить наше представление о том, что пространство непрерывно и представлять его как решетку, т.е. ввести дискретизацию. Дискретизация означает, что элемент пространства можно описать конечным числом, а время описывается прерывистыми скачками. Каким бы был в этом случае физический мир и как бы представлялась задача о его моделировании? Во-первых, возникла бы проблема того, что скорость света слегка зависела бы от направления; кроме того появились бы другие элементы анизотропии, которые можно было бы зарегистрировать экспериментально. Эта анизотропия могла бы быть очень малой. Конечно, физическое знание всегда неполно и всегда можно сказать, что можно построить модель, выводы которой лежат вне области, доступной на сегодняшний день. Можно предположить, что такая анизотропия будет обнаружена в будущем. С точки зрения физики было бы очень красиво, если можно предсказать новый результат, совместимый с существующими теориями и известными фактами и не находящий пока объяснения, но похоже, таких примеров в настоящее время нет (ситуация в физике в конце XIX - начале ХХ века была не такой - имелись экспериментальные результаты, несовместимые с физическими теориями). Поэтому возражений против анизотропии, в принципе, нет. Вопрос только в величине такой анизотропии.
Другой важный момент заключается в том, что законы природы обратимы, а правила компьютерных вычислений - нет. Однако это утверждение может быть оспорено - компьютерные вычисления могут быть сделаны обратимыми и соответствующие методы очень пригодятся нам в дальнейшем. Это то самое место, на котором изменяются взаимоотношения между физикой и вычислениями: появляются новые возможности для вычислений. Более того, возможно, что эти новые вычислительные возможности позволят нам понять что-то о физике.
Таким образом, правила моделирования, которые мы хотим построить, состоят в том, что число вычислительных элементов, необходимых для моделирования большой физической системы, пропорционально пространственно-временному объему физической системы. Т.е. если мы хотим объяснить что-то физически, мы можем сделать это точно и нам нужен компьютер определенного размера. Если удвоив объем пространства и времени нам потребуется компьютер экспоненциально большего размера, это будет рассматриваться как нарушение правил - тем самым мы устанавливаем правила игры.
Привычная для нас классическая логика является лишь частным случаем квантовой и справедлива для незначительной части реальности, описываемой классической физикой. Моментом зарождения квантовой логики, как самостоятельного направления в квантовой теории, можно считать 1936 год, когда Бирхгов и фон Нейман опубликовали статью «Логика квантовой механики»
Хотя чуть раньше, в 1932 году, фон Нейман в своей знаменитой книге «Математические основы квантовой механики» уже обратил внимание на возможность существования особой квантовой логики, обобщающей логику классическую: «Наряду с физическими величинами R существует еще нечто, являющееся предметом физики: именно альтернативные свойства системы L». То есть предметом физики являются не только некоторые конкретные физические величины, полученные при измерении, но и вся совокупность «непроявленных» результатов — тех, которые могли иметь место, но в данном случае не были реализованы.
Основное отличие квантовой логики от классической заключается в том, что в ней состояния физической системы определяются не только конкретными значениями связанных с системой наблюдаемых, но и всей совокупностью альтернативных свойств системы (суперпозицией состояний).
Квантовая логика существенно отличается от булевой. Например, не выполняется закон дистрибутивности в его общей форме. Дистрибутивность операций имеет место лишь для некоторых отдельных множеств, заданных на совместимых подпространствах гильбертова пространства. Дистрибутивный закон справедлив для попарно совместимых подпространств. С набором совместимых подпространств можно связать проекционные операторы и построить наблюдаемые, которые будут попарно коммутировать, и их можно представить как функцию одного оператора, то есть им соответствуют одновременно измеряемые величины.
Квантовая логика сейчас еще только разрабатывается, и пока трудно оценить все возможные последствия нового мышления, но одно несомненно — они будут очень значительны.
В этом отношении многое делается математиками, которые сейчас интенсивно работают над квантовыми алгоритмами и программами для квантового компьютера. Им в какой-то мере проще — не надо думать о физических ограничениях «на железо». Как только появится квантовый компьютер «в железе», у математиков уже будет в запасе большое количество готовых квантовых алгоритмов и программ.
Для реализации квантовых алгоритмов нужно небольшое число логических квантовых операторов (гейтов): однокубитные — NOT (логическое «Не»), преобразование Адамара (перевод кубита в нелокальное суперпозиционное состояние); двухкубитные — CNOT (контролируемое «Не»), SWAP (обмен состояниями) — и этого будет достаточно. С их помощью можно реализовать любые алгоритмы — не только классические, но и квантовые, которые реализуют квантовую логику.
Перечислим известные к настоящему времени квантовые алгоритмы.
Алгоритм Саймона или задача “Оракула”, 1997г. (экспоненциальное время при классических вычислениях и квадратичное время при квантовых). Он также известен под названием “алгоритм Дойча” (1985) и, наверное, является первым квантовым алгоритмом. Этот алгоритм решает задачу определения типа функции, глядя только на результат ее действия.
Алгоритм разложения на простые множители или алгоритм Шора, 1994 г. Для факторизации L - битового числа N лучший классический алгоритм асимптотически дает время
 .
Квантовый метод дает асимптотически
.
Квантовый метод дает асимптотически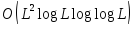 шагов. Заметим, что функция
шагов. Заметим, что функция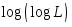 растет чрезвычайно медленно, поэтому
можно считать, что квантовый метод дает
растет чрезвычайно медленно, поэтому
можно считать, что квантовый метод дает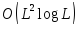 .
Ключевая идея этого алгоритма -
определение периода некой последовательности
с помощью Фурье - преобразования. Период
этой последовательности экспоненциально
зависит отL,
поэтому такой метод непрактичен для
обычных классических вычислений.
.
Ключевая идея этого алгоритма -
определение периода некой последовательности
с помощью Фурье - преобразования. Период
этой последовательности экспоненциально
зависит отL,
поэтому такой метод непрактичен для
обычных классических вычислений. Алгоритм поиска в базе данных (“алгоритм Гровера” 1997г.). Имеется список из N наименований. Классический алгоритм дает порядка N/2 обращений к базе данных для отыскания нужного наименования. Квантовый требует порядка
 обращений. Например, еслиN
= 104,
классический метод дает ответ примерно
за 5000 обращений, а квантовый - за 100. Если
же N
= 106,
то классический поиск потребует 5х105
обращений, а квантовый метод всего
1000!
обращений. Например, еслиN
= 104,
классический метод дает ответ примерно
за 5000 обращений, а квантовый - за 100. Если
же N
= 106,
то классический поиск потребует 5х105
обращений, а квантовый метод всего
1000!
