5.3. Открытые ключи

Теория шифрования с использованием открытого ключа была создана Уэтфилдом Диффи и Мартином Хеллманом в 1976 г. В этой системе Боб имеет общедоступный код для шифрования и закрытый код для расшифровки сообщений. Криптосистемы с открытым ключом основываются на так называемых односторонних функциях: по некоторому х легко вычислит функцию f(x), но, зная f(x), трудно вычислить x.

Первый алгоритм, основанный на теории Диффи-Хеллмана, был предложен Роном Райвестом, Эдди Шамиром и Леонардом Эдлманом в 1977 г. (RSA-алгоритм). Алгоритм RSA встроен в большинство операционных систем, а также во множество приложений, используемых в различных устройствах – от смарткарт до сотовых телефонов. Поэтому на этот продукт фирмы RSA Data Security Inc – программу, реализующую алгоритм шифрования с открытым ключом RSA, продано наибольшее количество лицензий – более 450 миллионов. Алгоритм RSA основан на разложении простого числа на множители. Известно, что вычислить произведение двух простых чисел легко. В то же время, обратная задача-разложение числа на простые множители, достаточно трудоёмка, поскольку время вычислений экспоненциально возрастает при увеличении количества битов в исходном числе. В системах с открытым ключом пользователям не надо договариваться о секретном ключе перед тем, как послать сообщение. Они работают по принципу сейфа с двумя ключами, так что есть один общий открытый ключ, чтобы его запереть, и ещё один секретный ключ, чтобы его отпереть. У всех есть ключ, запирающий сейф, но только у кого-то одного есть ключ, который снова его откроет, так что кто угодно может положить в сейф сообщение, но только один человек может его оттуда забрать. Криптосистему с открытым ключом можно пояснить с помощью механической аналогии, рис. 5.1.

Рис. 5.1. Механическая аналогия криптосистемы с открытым ключом

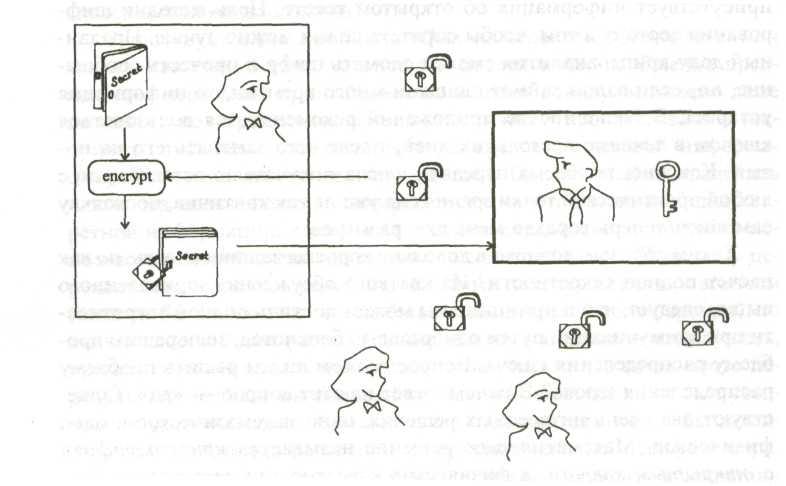
Пусть Алиса и Боб – два лица, которые хотят секретно общаться, а Ева их подслушивает. Пусть Боб может изготовить много висячих замков, и любой желающий послать Бобу секретное сообщение может получить открытый замок, который изготовил Боб. Открытый висячий замок можно рассматривать как открытый ключ. Один из них берёт себе Алиса. Как только Алиса закрыла замок, только Боб может его открыть, потому что только у него есть секретный ключ. Таким образом, Алиса может запереть любые данные по своему усмотрению и послать их Бобу с этим замком. Когда данные заперты, только Боб имеет к ним доступ благодаря наличию у него секретного ключа. Эти системы основаны на том факте, что некоторые математические операции легче провести в одном направлении, чем в другом. Поэтому в таких системах нет проблемы распределения ключей, однако, их надёжность основана на процедуре разложения больших целых чисел на простые множители (факторизации). Например, безопасность RSA, популярной системы с открытым ключом, основана на трудности факторизации больших чисел: чтобы факторизовать число из N десятичных цифр, компьютеру требуется число шагов, растущее экспоненциально с увеличением N, так что с увеличением N задача быстро становится неразрешимой.

Хотя в настоящее время не опубликованы быстрые алгоритмы решения задачи разложения числа на простые множители, нельзя утверждать, что они не существуют вовсе. Кроме того, вычислительная мощность компьютерных систем постоянно возрастает, поэтому сложность задачи не означает её неразрешимость. Один из последних отчётов компании RSA посвящён разложению 155-значного (512-битного) числа. Вычисления велись параллельно на многих компьютерах в течение семи месяцев в 1999 г. Если бы эта задача выполнялась на современном персональном компьютере, потребовалось бы 35,7 года. Оценки показывают, что с использованием даже тысячи современных рабочих станций и лучшего из известных вычислительных алгоритмов одно 250-значное число может быть разложено на множители примерно за 800 тысяч лет, а 1000-значное – за лет. (Для сравнения возраст Вселенной составляетлет). Поэтому криптографические алгоритмы, подобные RSA, оперирующие достаточно длинными ключами, считались абсолютно надёжными и использовались во многих приложениях. Однако, если появятся быстрые процедуры факторизации больших целых чисел, вся секретность и надёжность криптосистем с открытым ключом исчезнет.

Оказывается, используя законы квантовой механики, можно построить такие компьютеры, для которых задача факторизации не составит большого труда. По оценкам квантовый компьютер с памятью объёмом всего лишь около 10 тысяч квантовых битов способен разложить 1000-значное число на простые множители в течение всего нескольких часов.