
- •Теории управления квантовыми системами.
- •Содержание
- •Введение
- •1. Основные понятия и определения квантовой механики
- •1.1. Чистые и смешанные состояния
- •1. 2. Обозначения Дирака
- •1. 3. Перепутанные состояния
- •2. Элементы квантовой теории информации
- •2. 1. Кубиты
- •2. 2. О квантовой информации
- •2. 3. Преобразование одного кубита
- •2. 4. Перепутывание
- •2.5. Перепутывание и квантовая неразличимость
- •2.6. Логический элемент «управляемое не»
- •3. Парадокс эйнштейна – подольского – розена (эпр)
- •4. Неравенства белла
- •5. Квантовая криптография
- •5.1. Понятие о криптографии
- •5.2. Ключи и их распределение
- •5.3. Открытые ключи
- •5.4 Понятие о квантовой криптографии
- •5.4.1. Защита посредством неортогональных состояний
- •5.4.2. Защита посредством перепутывания
- •5.4.3. Практическая реализация квантово – криптографических систем
- •6. Квантовая телепортация
- •6.1 Общие представления
- •6.2. Протокол квантовой телепортации
- •6. 3. Обзор некоторых экспериментальных результатов по квантовой телепортации
- •6.4. Заключительные замечания: возможна ли телепортация макрообъекта?
- •7. Квантовые вычисления. Квантовые компьютеры.
- •7.1. Вводные замечания
- •7.2. Квантовый регистр
- •7.3. Задачи поиска.
- •7.4. Квантовые алгоритмы
- •7.4.1. Моделирование времени.
- •7.4.2. Моделирование вероятности
- •7.4.3. Алгоритм разложения на простые множители или алгоритм Шора
- •7.5. Общие требования к квантовым компьютерам Практическая реализация
- •Приложение. Гипотезы о квантовой природе сознания
- •Заключение
- •Словарь терминов
- •Литература
4. Неравенства белла
ЭПР – парадоксом А.Эйнштейн с соавторами пытались доказать, что квантовая механика неполна и не способна однозначно описать реальность в принципе. Отсюда возникло предположение о скрытых параметрах, которые помогут вернуться к привычному, локальному описанию объектов. Однако конечный результат исследования этой проблемы оказался противоположным. Выяснилось, что более правильным является именно квантовомеханический подход, и результат такого подхода несовместим с предположением, что наблюдаемые свойства объекта существуют до наблюдения как объективная самостоятельная внутренняя характеристика.
Первый реальный шаг к такому выводу сделал Белл в 1964 году, когда он, анализируя ситуацию со скрытыми параметрами, сформулировал свои знаменитые неравенства. Он ввел понятие «объективной локальной теории», которой придерживались Эйнштейн и другие сторонники скрытых параметров. В этой теории предполагается, что
● физические свойства системы существуют сами по себе, они объективны и не зависят от измерения;
● измерение одной системы не влияет на результат измерения другой системы;
● поведение не взаимодействующей с окружением системы зависит лишь от условий в более ранние моменты времени.
Это привычные для всех нас классические представления об окружающей реальности.
Теорема Белла утверждает, что «объективная локальная теория» и квантовая механика дают разные предсказания для результатов измерения. Естественно, возник вопрос, каким же на самом деле является реальный мир, и неравенства Белла помогли ответить на него непосредственно — на основании анализа результатов экспериментов. Такие эксперименты были проведены А. Аспектом в 1982 году и впоследствии многими другими исследователями. Их результаты показали, что окружающая нас реальность является квантовой в своей основе, и все вышеперечисленные предположения «объективной локальной теории» в общем случае несправедливы.
Физических экспериментов по проверке локального реализма было проведено очень много, и все они опровергают положения «объективной локальной теории», свидетельствуя в пользу нелокальности окружающей нас реальности.
Одним из наиболее ярких экспериментов стал эксперимент, проведённый в 2000 году (Pan J-W., Bouwmeester D., Daniell M., Weinfurter H. and Zeilinger A. Experimental test of quantum nonlocality in three-photon Greenberger-Horne-Zeilinger entanglement, Nature 403, 515, 2000). В этом эксперименте исследовались трехчастичные запутанные состояния (так называемые ГХЦ-состояния — Гринбергера, Хорна, Цайлингера), которые позволяют дать достоверный результат по проверке локального реализма.
Гринбергер, Хорн и Цайлингер показали, что квантовомеханические предсказания некоторых результатов измерений трех запутанных частиц противоречат локальному реализму в случаях, когда квантовая теория дает достоверные предсказания.
В этом эксперименте в качестве элементов реальности рассматривались циркулярные поляризации фотонов. Предположим, что элементы реальности существуют до того, как проведено измерение. Значит, мы можем определить все возможные исходы (в данном случае — четыре). Это конкретные математические выражения, полученные как следствие сделанного предположения. То есть «локальный реалист» утверждает, что в эксперименте будут получены именно эти результаты, один из четырех в каждом частном случае.
С другой стороны, можно записать аналогичные формулы для возможных исходов эксперимента, предсказанных квантовой теорией. Последние прямо противоположны первым. Тут уж экспериментаторам трудно ошибиться. Всякий раз, когда локальный реализм предсказывает достоверный специфический результат измерения одного фотона (при данном результате измерения двух других), квантовая физика достоверно предсказывает прямо противоположный результат.
Эксперименты подтверждают, что поляризацию фотонов для ГХЦ-состояний нельзя разделить на части и сопоставить с отдельными элементами реальности. По спиновым степеням свободы система составляет единое целое. Утверждения локальной объективной теории оказываются несправедливыми. Выходит, что реальность является более сложной, чем это представляется локальным реалистам.
Эксперименты по квантовой нелокальности были проведены не только с состояниями, запутанными по поляризации, но также и по времени, по импульсам и т. д., и все они подтвердили наличие нелокальности на фундаментальном уровне реальности.
После того как Белл сформулировал свою теорему, стало очевидным, что квантовая механика несовместима с локальным реализмом. В настоящее время нарушение неравенства Белла (или его аналогов) считается одним из основных факторов, свидетельствующих о наличии значительных квантовых корреляций в системе и, как следствие, невозможности описания такой системы в рамках классического подхода. Наличие запутанности в системе является необходимым условием для нарушения неравенства Белла.
Сейчас акценты, как экспериментаторов, так и теоретиков, сместились в сторону прикладных исследований и технического применения нелокальных квантовых корреляций. Значительные усилия в последнее время были направлены на то, чтобы понять роль запутанных состояний в природе, на возможность их практического применения в качестве принципиально нового нелокального ресурса в технических устройствах.
Экспериментаторы работают сейчас над созданием квантового компьютера, квантово-криптографических систем и других квантово-когерентных устройств. А теоретики, основываясь на этих экспериментах, ищут наиболее удобные способы количественного описания квантовой запутанности и процессов декогеренции / рекогеренции. В частности, идет интенсивный поиск наиболее удобной в практическом применении меры квантовой запутанности.
Рассмотрим мысленный эксперимент ЭПР, схема которого показана на рис. 4.1.
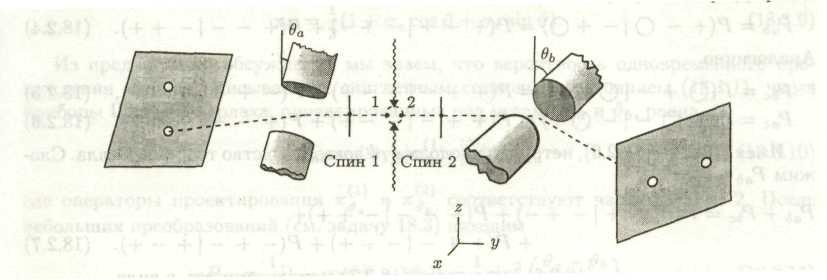
Система
со спином, равным 0, например, ортоводород,
расщепляется внешним полем. Две частицы
со спином 1/2 (протоны) распространяются
в противоположных направлениях и
проходят через приборы Штерна – Герлаха,
ориентированные под углом
![]() к вертикали (+z) для частицы 1 и под углом
к вертикали (+z) для частицы 1 и под углом![]() для частицы 2. Для примера показано, что
частица со спином вверх «пройдёт» через
нижнее отверстие. Рассмотрим вероятность
указанного процесса P(
для частицы 2. Для примера показано, что
частица со спином вверх «пройдёт» через
нижнее отверстие. Рассмотрим вероятность
указанного процесса P(![]() ,
,![]() )
)![]() Pab.
Введём обозначение
Pab.
Введём обозначение
![]() (4.1)
(4.1)
Левая
часть скобки относится к частице 1, а
правая – к частице 2. В каждой части –
три позиции, зарезервированные для
информации по прохождению через ПШГ,
ориентированный под углом
![]() ,
соответственно. Знак «+» соответствует
прохождению, знак «-» - блокированию,
знак «0» означает, что эта совместная
вероятность не содержит информацию о
прохождении при данном значении угла,
именно: первый знак + означает, что
частица 1 проходит через ПШГ, ориентированный
под углом
,
соответственно. Знак «+» соответствует
прохождению, знак «-» - блокированию,
знак «0» означает, что эта совместная
вероятность не содержит информацию о
прохождении при данном значении угла,
именно: первый знак + означает, что
частица 1 проходит через ПШГ, ориентированный
под углом
![]() , но частица 2 при этом не проходит через
ПШГ, ориентированный под углом
, но частица 2 при этом не проходит через
ПШГ, ориентированный под углом![]() ,
что отмечено знаком -; аналогично, если
частица 2 проходит через ПШГ, ориентированный
под углом
,
что отмечено знаком -; аналогично, если
частица 2 проходит через ПШГ, ориентированный
под углом![]() ,
знак + помещается во вторую позицию в
правой части и, следовательно, знак –
помещается во вторую позицию в левой
части, относящейся к частице 1. Таким
образом,Pab
обозначает вероятность того, что частица
1 пройдёт через ПШГ1,
ориентированный под углом
,
знак + помещается во вторую позицию в
правой части и, следовательно, знак –
помещается во вторую позицию в левой
части, относящейся к частице 1. Таким
образом,Pab
обозначает вероятность того, что частица
1 пройдёт через ПШГ1,
ориентированный под углом
![]() к оси z , а частица 2 пройдёт через ПШГ2,
ориентированный под углом
к оси z , а частица 2 пройдёт через ПШГ2,
ориентированный под углом
![]() к вертикальному направлению. Аналогично
к вертикальному направлению. Аналогично
![]() (4.2)
(4.2)
![]() (4.3)
(4.3)
Хотя вероятность
совместных событий Pab
ничего не говорит о прохождении частиц
при другом угле
![]() ,
известно, что для любой заданной частицы
сумма вероятности прохождения её через
ПШГ, ориентированный под углом
,
известно, что для любой заданной частицы
сумма вероятности прохождения её через
ПШГ, ориентированный под углом![]() к вертикали, и вероятности непрохождения
её через этот прибор, равна 1. Тогда,
учитывая также антикорреляцию проекций
спина, можно записать
к вертикали, и вероятности непрохождения
её через этот прибор, равна 1. Тогда,
учитывая также антикорреляцию проекций
спина, можно записать
![]() =
=![]() +
+![]() (4.4)
(4.4)
Аналогично
![]() =
=![]() +
+![]() (4.5)
(4.5)
![]()
![]() +
+![]() (4.6)
(4.6)
Сложив (4.4) и (4.5) получим
Pab
+ Pbc=![]() +
+![]() +
+![]() +
+![]() (4.7)
(4.7)
C учётом (4.6) выражение (4.7) можно записать
Pab
+ Pbc=
![]() +
+![]() +
+![]() (4.8)
(4.8)
Поскольку вероятности должны быть положительными получим неравенство Белла
Pab
+ Pbc![]() Pac (4.9)
Pac (4.9)
Квантовое вычисление
вероятности прохождения частицы со
спином 1/2, описываемой вектором состояния
![]() ,
через ПШГ, ориентированный под углом
,
через ПШГ, ориентированный под углом![]() ,
осуществляется по формуле
,
осуществляется по формуле
![]() , (4.10)
, (4.10)
где состояние
![]() получается вращением состояния «спин
вверх» вокруг оси y:
получается вращением состояния «спин
вверх» вокруг оси y:
![]() =
=![]() . (4.11)
. (4.11)
Напомним, что матрицы
![]()
![]()
![]() (4.12)
(4.12)
![]() ,
,
![]() (4.13)
(4.13)
Выражение (4.10) можно переписать в виде
![]()
![]() . (4.14)
. (4.14)
Определим оператор проектирования
![]() (4.15)
(4.15)
С учётом (4.11) это выражение можно записать следующим образом:
![]() (4.16)
(4.16)
Применяя соотношение
 (4.17)
(4.17)
находим, что (4.17) принимает вид
![]() . (4.18)
. (4.18)
Вероятность
одновременного прохождения частиц,
описываемых синглетным спиновым
состоянием (3.1), через приборы Штерна –
Герлаха, ориентированные под углами
![]() ,
равна
,
равна
![]() , (4.19)
, (4.19)
где операторы
проектирования
![]() соответствуют
частицам 1 и 2. После преобразований
находим
соответствуют
частицам 1 и 2. После преобразований
находим
![]() (4.20)
(4.20)
Теперь можно использовать этот результат для проверки того, удовлетворяет ли квантовая механика теореме Белла, т.е. справедлива ли квантовая версия неравенства Белла (4.9):
![]() +
+![]() (4.21)
(4.21)
Для ответа на
поставленный вопрос достаточно
рассмотреть лишь углы
![]() ,
при которых (4.21) означает, что
,
при которых (4.21) означает, что
![]()
или 0,15![]() 0,25,
что неверно. Следовательно, квантовая
механика нарушает неравенство Белла.
0,25,
что неверно. Следовательно, квантовая
механика нарушает неравенство Белла.
Таким образом, получается, что предсказания квантовой механики и гипотезы скрытых параметров не согласуются между собой. Было поставлено много экспериментов, доказавших невозможность скрытых параметров и, следовательно, подтвердивших полноту квантовой механики в обсуждаемом смысле.
Около 20 лет назад обсуждаемые вопросы считались, в основном, философскими, хотя, конечно, и имеющими отношение к пониманию «устройства» микромира. За последние 10 лет, однако, базовые понятия квантовой суперпозиции и квантового перепутывания оказались ключевыми составляющими в новых системах квантовой коммуникации и квантовых вычислений. Так, белловские состояния являются "рабочим инструментом" теории квантовой информатики.
