
- •Теории управления квантовыми системами.
- •Содержание
- •Введение
- •1. Основные понятия и определения квантовой механики
- •1.1. Чистые и смешанные состояния
- •1. 2. Обозначения Дирака
- •1. 3. Перепутанные состояния
- •2. Элементы квантовой теории информации
- •2. 1. Кубиты
- •2. 2. О квантовой информации
- •2. 3. Преобразование одного кубита
- •2. 4. Перепутывание
- •2.5. Перепутывание и квантовая неразличимость
- •2.6. Логический элемент «управляемое не»
- •3. Парадокс эйнштейна – подольского – розена (эпр)
- •4. Неравенства белла
- •5. Квантовая криптография
- •5.1. Понятие о криптографии
- •5.2. Ключи и их распределение
- •5.3. Открытые ключи
- •5.4 Понятие о квантовой криптографии
- •5.4.1. Защита посредством неортогональных состояний
- •5.4.2. Защита посредством перепутывания
- •5.4.3. Практическая реализация квантово – криптографических систем
- •6. Квантовая телепортация
- •6.1 Общие представления
- •6.2. Протокол квантовой телепортации
- •6. 3. Обзор некоторых экспериментальных результатов по квантовой телепортации
- •6.4. Заключительные замечания: возможна ли телепортация макрообъекта?
- •7. Квантовые вычисления. Квантовые компьютеры.
- •7.1. Вводные замечания
- •7.2. Квантовый регистр
- •7.3. Задачи поиска.
- •7.4. Квантовые алгоритмы
- •7.4.1. Моделирование времени.
- •7.4.2. Моделирование вероятности
- •7.4.3. Алгоритм разложения на простые множители или алгоритм Шора
- •7.5. Общие требования к квантовым компьютерам Практическая реализация
- •Приложение. Гипотезы о квантовой природе сознания
- •Заключение
- •Словарь терминов
- •Литература
6.2. Протокол квантовой телепортации
Под протоколом понимается последовательность манипуляций, приводящих к решению поставленной задачи.
Рассмотрим схему по квантовой телепортации, предоженную Беннетом, Брассардом, Крепэ, Джозсой, Пересом и Вуттерсом в 1993 г. и представленную на рис. 6.1
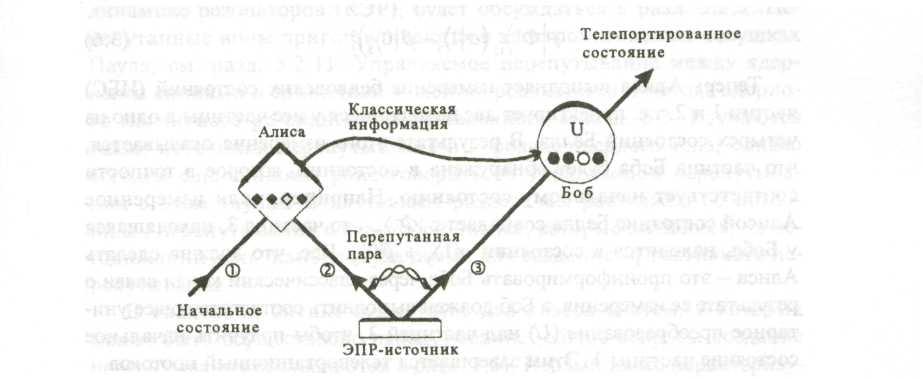
Пусть у Алисы есть
частица в определённом квантовом
состоянии – кубит
![]() ,
где |0
,
где |0![]() и |1
и |1![]() - два ортогональных состояния с
комплексными амплитудами
- два ортогональных состояния с
комплексными амплитудами![]() и
и![]() ,
связанные условием нормировки
,
связанные условием нормировки![]() .
Алисе нужно передать Бобу это квантовое
состояние, но она не может доставить
частицу непосредственно. Как известно
из квантовой механики любое квантовое
измерение, выполненное Алисой над её
частицей, неминуемо разрушит квантовое
состояние без получения полной информации,
необходимой Бобу для воссоздания
исходного состояния. Для передачи
квантового состояния необходимо
использовать вспомогательную ЭПР - пару
перепутанных частиц 2 и 3. Частица 2
вручается Алисе, а частица 3 посылается
Бобу. Пусть перепутанная пара частиц 2
и 3, распределённая между Алисой и Бобом,
находится в состоянии
.
Алисе нужно передать Бобу это квантовое
состояние, но она не может доставить
частицу непосредственно. Как известно
из квантовой механики любое квантовое
измерение, выполненное Алисой над её
частицей, неминуемо разрушит квантовое
состояние без получения полной информации,
необходимой Бобу для воссоздания
исходного состояния. Для передачи
квантового состояния необходимо
использовать вспомогательную ЭПР - пару
перепутанных частиц 2 и 3. Частица 2
вручается Алисе, а частица 3 посылается
Бобу. Пусть перепутанная пара частиц 2
и 3, распределённая между Алисой и Бобом,
находится в состоянии
![]() (6.1)
(6.1)
Важное свойство
этого перепутанного состояния состоит
в том, что как только измерение одной
из частиц проектирует её определённое
состояние, которое может быть любой
нормированной линейной суперпозицией
состояний |0![]() и |1
и |1![]() ,
другая частица должна оказаться в
ортогональном состоянии. Специфическое
фазовое соотношение между двумя членами
в правой части (6.1) (здесь разность фаз
равна
,
другая частица должна оказаться в
ортогональном состоянии. Специфическое
фазовое соотношение между двумя членами
в правой части (6.1) (здесь разность фаз
равна![]() ,
что проявляется в знаке "минус")
подразумевает, что утверждение об
ортогональности не зависит от базиса,
выбранного для поляризационного
измерения.
,
что проявляется в знаке "минус")
подразумевает, что утверждение об
ортогональности не зависит от базиса,
выбранного для поляризационного
измерения.
Таким образом, у Алисы находится квантовая система - частица 1 в начальном состоянии, которую она хочет передать Бобу. Алиса и Боб имеют также по одной частице из вспомогательной пары частиц 2 и 3, испущенной ЭПР – источником. Затем, Алиса выполняет совместное измерение состояния Белла над начальной частицей и имеющейся у неё частицей из вспомогательной пары. Результатом измерения является проектирование обеих частиц в перепутанное состояние. Под измерением белловских состояний (ИБС) подразумевается не столько акт физической регистрации частиц, сколько некая операция, в результате которой приготавливается перепутанное состояние двух частиц, т.е. одно из четырёх состояний Белла:
|![]() +
+![]() 12
=
12
=![]() |0
|0![]() 1|1
1|1![]() 2
+ 1
2
+ 1![]() 1|0
1|0![]() 2) (6.2)
2) (6.2)
|![]()
![]() 12
=
12
=![]() |0
|0![]() 1|1
1|1![]() 2
_
1
2
_
1![]() 1|0
1|0![]() 2) (6.3)
2) (6.3)
|![]()
![]() 12
=
12
=![]() |0
|0![]() 1|0
1|0![]() 2
+ 1
2
+ 1![]() 1|1
1|1![]() 2) (6.4)
2) (6.4)
|![]()
![]() 12
=
12
=![]() |0
|0![]() 1|0
1|0![]() 2
- 1
2
- 1![]() 1|1
1|1![]() 2) (6.5)
2) (6.5)
После этого Алиса посылает Бобу по классическому каналу связи результат своего измерения, и он выполняет унитарное преобразование над другой (своей) частицей вспомогательной пары; эта частица теперь имеет в точности такое же состояние, как и у начальной частицы. В случае кантовой телепортации кубита, Алиса выполняет проекционное измерение в четыре ортогональных состояния (белловские состояния), которые образуют полный базис. Сообщение Бобу результата измерения Алисы, т.е. два бита классической информации, даёт ему возможность воссоздать начальный кубит. Хотя первоначально частицы 1 и 2 не являются перепутанными, их совместное поляризационное состояние может всегда быть представлено в идее суперпозиции четырёх максимально перепутанных состояний Белла (6.2) – (6.5), поскольку эти состояния образуют полный ортонормированный базис. Общее состояние частицы 3 записывается в виде:
|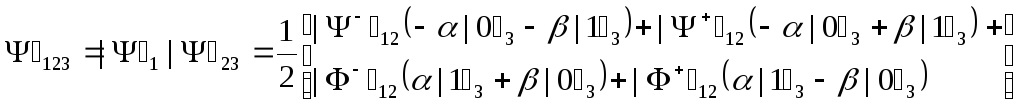 (6.6)
(6.6)
Теперь Алиса
выполняет измерение белловских состояний
частиц 1 и 2, т.е. проектирует две находящиеся
у неё частицы в одно из четырёх состояний
Белла. В результате этого измерения
оказывается, что частица Боба будет
обнаружена в состоянии, которое в
точности соответствует начальному
состоянию. Например, если измеренное
Алисой состояние Белла совпадает с |![]() ,
то частица 3, находящаяся у Боба, находится
в состоянии
,
то частица 3, находящаяся у Боба, находится
в состоянии![]() .
Всё, что должна сделать Алиса – это
проинформировать Боба через классический
канал связи о результате её измерения,
а Боб должен выполнить соответствующее
унитарное преобразование над частицей
3, чтобы получить начальное состояние
частицы 1. Этим завершается протокол.
.
Всё, что должна сделать Алиса – это
проинформировать Боба через классический
канал связи о результате её измерения,
а Боб должен выполнить соответствующее
унитарное преобразование над частицей
3, чтобы получить начальное состояние
частицы 1. Этим завершается протокол.
Во время процедуры
телепортации значения
![]() остаются неизвестными. Из своих измерений
состояний Белла Алиса не получает
никакой информации о телепортируемом
состоянии. Единственное, что достигается
при ИБС – это передача квантового
состояния. Во время ИБС частица 1 теряет
своё начальное квантовое состояние,
т.к. она перепутывается с частицей 2.
Поэтому состояние
остаются неизвестными. Из своих измерений
состояний Белла Алиса не получает
никакой информации о телепортируемом
состоянии. Единственное, что достигается
при ИБС – это передача квантового
состояния. Во время ИБС частица 1 теряет
своё начальное квантовое состояние,
т.к. она перепутывается с частицей 2.
Поэтому состояние![]() разрушается Алисой при телепортации,
что удовлетворяет требованию теоремы
о запрете клонирования. Более того,
начальное состояние частицы 1 может
быть совершенно неизвестно не только
Алисе, но и вообще кому бы то ни было.
Состояние могло бы быть квантово –
механически полностью неопределенно
в то время, когда происходит измерение
состояния Белла. Это случай, когда
частица 1 является частью перепутанной
пары и поэтому сама по себе не имеет
определённых свойств. Это приводит к
обмену перепутыванием.
разрушается Алисой при телепортации,
что удовлетворяет требованию теоремы
о запрете клонирования. Более того,
начальное состояние частицы 1 может
быть совершенно неизвестно не только
Алисе, но и вообще кому бы то ни было.
Состояние могло бы быть квантово –
механически полностью неопределенно
в то время, когда происходит измерение
состояния Белла. Это случай, когда
частица 1 является частью перепутанной
пары и поэтому сама по себе не имеет
определённых свойств. Это приводит к
обмену перепутыванием.
