4.3. Свойства определителей

Для того чтобы вычислять определители порядков, больших, чем 3, используют свойства определителей и теорему Лапласа.

Теорема 4.1 (Лапласа). Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения, т. е.

 = а_i1А_i1 + а_i2А_i2 + … + а_inА_in, где i = 1, 2, …, n (разложение определителя по элементам i-ой строки);

 = а_1jА_1j + а_2jА_2j + … + а_njА_nj, где j = 1, 2, …, n (разложение определителя по элементам j-го столбца).

Перечислим основные свойства определителей.

1. Если какая-либо строка (столбец) матрицы состоит из одних нулей, то определитель этой матрицы равен нулю.

2. Определитель диагональной матрицы равен произведению ее диагональных элементов.

3. Определитель треугольной (верхнетреугольной или нижнетреугольной) матрицы равен произведению элементов ее главной диагонали.

4. При перестановке двух строк (столбцов) матрицы ее определитель меняет знак на противоположный.

5. Если квадратная матрица содержит две одинаковые строки (столбца), то ее определитель равен нулю.

6. Если все элементы какой- либо строки (столбца) определителя умножить на некоторое число k, то определитель умножается на это число k. (Общий множитель элементов строки (столбца) можно выносить за знак определителя.)

7. Если квадратная матрица содержит две пропорциональные строки (столбца), то ее определитель равен нулю.

8. Определитель матрицы не изменится, если к элементам какой-либо строки (столбца) матрицы прибавить элементы другой строки (столбца) матрицы, предварительно умноженные на одно и то же число.

9. При транспонировании матрицы ее определитель не меняется.

10. Определитель произведения двух квадратных матриц равен произведению их определителей.

11. Сумма произведений элементов какой-либо строки (столбца) матрицы на алгебраические дополнения элементов другой строки (столбца) этой матрицы равна нулю.

4.4. Практическое вычисление определителей

Один из способов вычисления определителей порядка выше трех – разложение его по какому-либо столбцу или строке.

Пример 4.4. Вычислить определитель  = .

Решение. Разложим данный определитель по третьей строке:

= а₃₁А₃₁ + а₃₂А₃₂ + а₃₃А₃₃ + а₃₄А₃₄ = 

= 2(–1)^3 + 1М₃₁ ++ 0(–1)^3 + 2М₃₂ + 1(–1)^3 + 3М₃₃ + (–1)(–1)^3 + 4М₃₄ =

= 21 + 0 + 11 + (–1)(–1) =

= 2(9 + 20 + 6 – 30 + 12 + 3) + (9 – 4 – 50 – 2 + 60 + 15) + (9 + 3 + 25 + 1 – – 45 + 15) = 40 + 28 + 8 = 76.

При вычислении определителей целесообразно так преобразовать исходную матрицу с помощью свойств определителей, чтобы в преобразованной матрице получилась строка (столбец), содержащая максимальное число нулей («обнулить» строку), а потом найти определитель разложением по этой строке (столбцу). В ходе преобразований необходимо следить за тем, чтобы значение определителя не менялось.

Пример 4.5. Вычислить определитель четвертого порядка:  = .

Решение. В третьей строке уже есть один ноль. Если к 1-ому столбцу прибавить 3-ий, умноженный на (-4), а ко 2-му столбцу прибавить 3-ий, умноженный на 2, то получим следующий определитель, который разложим по элементам 3-ей строки (теорема Лапласа):

= а₃₃(–1)^3 + 3M₃₃ = 1(–1)^3 + 3.

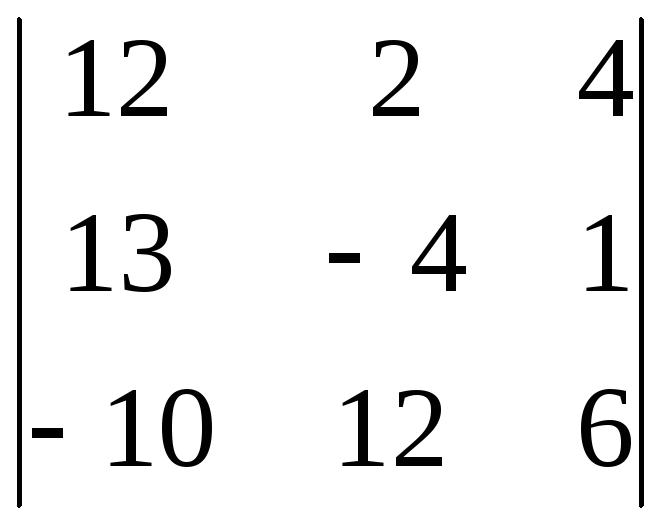Полученный определитель можно вычислить по правилу треугольника или продолжить упрощение матрицы с последующим применением теоремы Лапласа. Прибавим к 1-ой строке 2-ую, умноженную на (–4), а к 3-ей строке 2-ую, умноженную на (–6), и получим такой определитель:  = 1(–1)^2 + 3  = –144.