
ТОЭ / ТОЭ ТУСУР
.pdf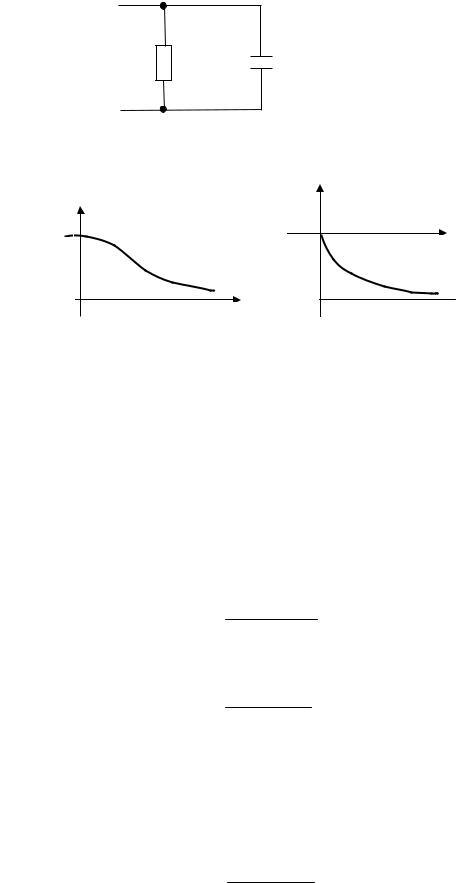
70
|
R |
C |
|
|
а |
|
|
|
|
ϕ(ω) |
|
z (ω) |
|
|
|
|
ϕ(ω) |
|
|
|
|
|
|
|
|
0 |
ω |
|
|
||
|
|
|
|
0 |
ω |
−π |
|
2 |
|
||
|
б |
|
в |
|
Рис. 49 |
|
|
Передаточная комплексная функция (комплексный ко-
эффициент передачи) цепи определяет реакцию цепи на внешнее воздействие и равна отношению выходной величины (напряжение, ток) к входной величине (напряжение, ток), выраженных в комплексной форме.
Различают четыре вида передаточных функций:
– передаточная функция по напряжению
Kи( jω) = Uвых( jω) ; Uвх( jω)
– передаточная функция по току
KI ( jω) = Iвых( jω) ; Iвх( jω)
– передаточное сопротивление |
|
||
Kz ( jω) = |
Uвых( jω) |
; |
|
Iвх( jω) |
|||
|
|
||
– передаточная проводимость
KY ( jω) = Iвых( jω) . Uвх( jω)
71
Зависимость модуля передаточной функции K (ω) от часто-
ты называется амплитудной частотной характеристикой
(АЧХ), зависимость аргумента передаточной функции ϕ(ω) —
фазовой частотной характеристикой (ФЧХ). На комплексной плоскости можно построить геометрическое место конца вектора
K ( jω) при изменении частоты — амплитудно-фазовую частотную характеристику (АФЧХ).
3.7 Явление резонанса
Пусть пассивный двухполюсник содержит одну или несколько индуктивностей и одну или несколько емкостей (и, конечно, активные сопротивления). Под резонансным режимом работы такого двухполюсника понимают режим, при котором входное сопротивление двухполюсника является чисто активным.
По отношению к внешней цепи двухполюсник в резонансном режиме ведет себя как активное сопротивление, поэтому ток и напряжение на его входе совпадают по фазе. Реактивная мощность двухполюсника при этом равна нулю.
Различают две основные разновидности резонансных режимов: резонанс токов и резонанс напряжений.
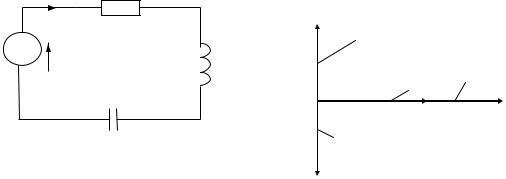
Резонанс напряжений возникает в последовательной RLC- цепи, представленной на рис. 50, а.
R
I
~ E |
jωLI |
||
L |
|
U R I |
|
C |
|
|
|
− j |
I |
|
|
ωC |
|||
|
|||
а |
|
б |
|
Рис. 50 |
|
|
|
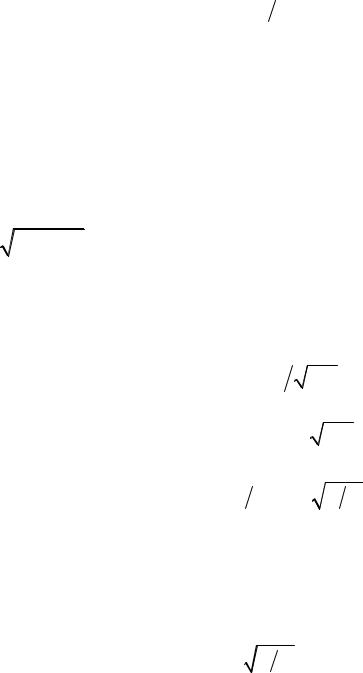
72
При резонансе ток в цепи должен совпадать по фазе с э.д.с. E . Это возможно, если входное сопротивление схемы Z = R + j(ωL −1 ωC) будет чисто активным. Условие наступления резонанса в схеме (см. рис. 50, а)
ωC) будет чисто активным. Условие наступления резонанса в схеме (см. рис. 50, а)
ωL =1 ωC. |
(43) |
Здесь значения противоположных по фазе напряжений на индуктивности и емкости равны, как показано на диаграмме (рис. 50, б), поэтому резонанс в последовательной цепи получил название резонанса напряжений.
Напряжения на индуктивности и емкости при резонансе могут значительно превышать напряжение на входных зажимах, которое равно напряжению на активном сопротивлении.
Полное сопротивление цепи z при Х = 0 минимально: z = R2 + X 2 = R , а ток I максимален.
Резонанса можно достичь, изменяя один из трех параметров: ω, L или С. Угловая частота, при которой наступает резонанс, называется угловой резонансной частотой и определяется из усло-
вия (43): |
|
ω0 =1 LC. |
(44) |
Соответственно резонансная частота
f 0 =1 2π LC.
2π LC.
Индуктивное и емкостное сопротивления при резонансе —
ω0 L =1 ω0C = L C = ρ.
Величина ρ называется характеристическим сопротивлением. Напряжения на реактивных элементах —
U L =U C = ω0LI = ω0L E. R
Отношение
ω0L |
= |
L C |
= |
ρ |
= Q |
(45) |
|
R |
R |
R |
|||||
|
|
|
|
называется добротностью резонансного контура. Добротность показывает, во сколько раз напряжение на индуктивном (емкостном) элементе превышает напряжение на входе схемы в резонансном режиме.
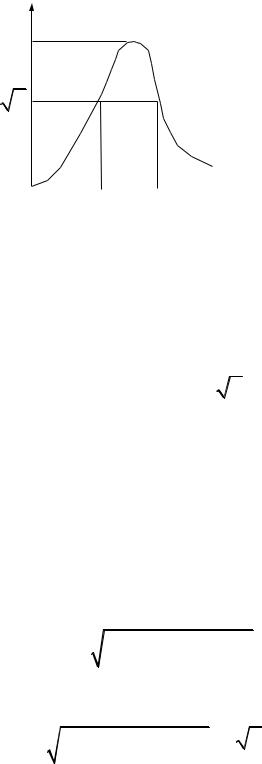
73
Примерный вид зависимости тока от частоты для рассматриваемой схемы (при неизменном значении Е) представлен на рис. 51 и называется амплитудной частотной характеристикой.
I I p
I p
1
1 2
2
0 
ωн ωв ω
Рис. 51
График АЧХ показывает, что последовательная RLC-цепь (последовательный резонансный контур) обладает избирательными свойствами, которые характеризуются полосой пропускания. Полоса пропускания П = ωв −ωн определяется из условия,
что ток на частотах ωн и ωв уменьшается в 2 раз по сравнению с током при резонансе. Здесь частоты ωн и ωв являются соответ-
ственно нижней и верхней границами полосы пропускания. Установим связь между добротностью, полосой пропуска-
ния и резонансной частотой.
Комплекс действующего значения тока в цепи I , действующее значение тока в цепи I и действующее значение тока при резонансе I p соответственно равны:
I = |
E |
|
; |
I = |
|
E |
|
|
|
|
|
; I = |
E |
. |
||||
R + j ( X L − XC ) |
2 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
p |
R |
|||||
|
|
|
|
|
|
|
R +( X L − XC ) |
2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
На границах полосы пропускания |
|
|
|
1 |
|
|
|
|
||||||||||
|
|
I |
= |
|
|
R |
|
= |
|
. |
|
|
|
|||||
|
|
I p |
R |
2 |
+( X L − XC ) |
2 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Отсюда
2R2 = R2 +( X L − XC )2
74 |
|
и окончательно |
|
R = ±( X L − XC ). |
(46) |
В (46) знак «минус» перед скобкой соответствует нижней, а знак «плюс» — верхней границам полосы пропускания.
Из (45) выразим
R = ω0 L Q
и подставим в (46) для нижней границы полосы пропускания, используя параметры реактивных элементов:
|
|
|
|
ω0 L = −ω L + |
|
|
1 |
. |
|
|||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
Q |
|
|
|
|
|
н |
|
|
|
ω |
C |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
н |
|
|
|
Поделив последнее равенство на L и подставив из (44) |
||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
= ω2 , |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
LC |
|
|
|
|
0 |
|
|
|
|||
получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
ω2 + ω0 ω −ω2 |
|
|
|
|
||||||||||||||
|
|
|
|
= 0. |
|
|||||||||||||||
|
|
|
|
н |
|
Q |
|
|
|
н |
|
|
0 |
|
|
|
|
|||
Положительный корень решения этого уравнения дает ниж- |
||||||||||||||||||||
нюю границу полосы пропускания: |
|
|
|
|
|
|
||||||||||||||
|
− |
ω0 |
+ |
ω02 |
|
|
2 |
|
|
|
|
− |
ω |
|
ω |
|
||||
|
|
Q2 |
+ 4ω0 |
|
|
|
0 |
+ 0 1+ 4Q2 |
|
|||||||||||
ω = |
Q |
|
|
|
|
|
= |
|
|
|
Q |
|
Q |
= |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
н |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||
|
|
|
|
= |
|
ω0 |
( 1+ 4Q2 −1). |
(47) |
||||||||||||
|
|
|
|
|
2Q |
|||||||||||||||
Аналогично находится верхняя граница полосы пропуска- |
||||||||||||||||||||
ния: |
|
|
|
|
|
|
ω0 |
( |
|
1+ 4Q2 +1). |
|
|||||||||
|
|
|
|
ωв == |
|
|
(48) |
|||||||||||||
|
|
|
|
|
2Q |
|
||||||||||||||
С учетом (47) и (48) полоса пропускания определяется сле- |
||||||||||||||||||||
дующим выражением: |
П = ω −ω = ω0 . |
|
||||||||||||||||||
|
|
|
|
(49) |
||||||||||||||||
|
|
|
|
|
|
|
в |
н |
|
|
Q |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||

75
Из (49) следует, что для последовательного резонансного контура чем больше добротность, тем уже полоса пропускания, т.е. лучше избирательность.
Если при резонансе эквивалентное сопротивление цепи чисто активное, а ток и приложенное напряжение совпадают по фазе, то при ω ≠ ω0 наблюдается следующее.
На частотах меньше резонансной реактивное сопротивление
цепи
X = X − X |
|
= ωL − |
1 |
|
ωC |
||
L |
C |
|
|
|
|
будет иметь емкостный характер, так как реактивное сопротивление конденсатора больше реактивного сопротивления индуктивности, а при частотах больше резонансной уже сопротивление индуктивности станет больше сопротивления конденсатора, и реактивное сопротивление цепи примет индуктивный характер. В соответствии с этим при частотах меньше резонансной ток в цепи опережает приложенное напряжение (угол ϕ положителен) и при
частотах больше резонансной — отстает от напряжения отрицателен).
Для расчета угла ϕ используется формула:
|
|
|
ωL − |
1 |
|
|
|
ϕ = arctg |
X |
= arctg |
ωC |
. |
|||
|
|||||||
|
R |
|
|||||
|
R |
|
|
|
|||
(угол ϕ
(50)
Вчастном случае на границах полосы пропускания с учетом
(46)получим:
ϕн = arctg −( X L − XC ) = 45°;
R
ϕв = arctg X L − XC = −45°.
R
Здесь обозначено: ϕн и ϕв — соответственно начальная фа-
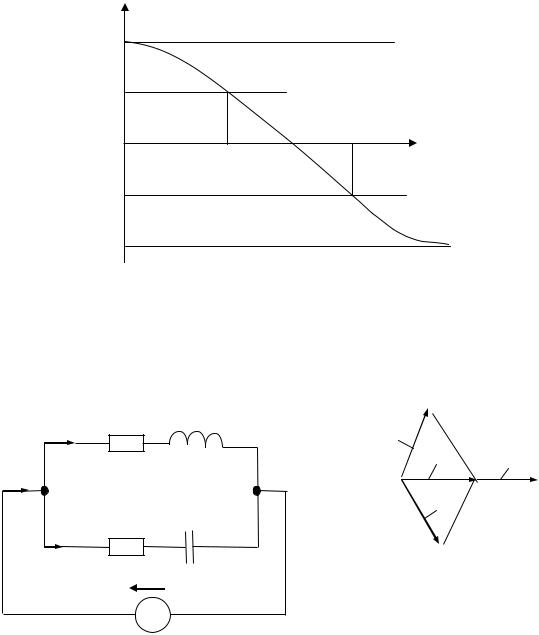
за тока на нижней и верхней границах полосы пропускания. Построенный по (50) график называется фазовой частотной
характеристикой (ФЧХ).
Примерный вид фазовой частотной характеристики приведен на рис. 52.
76
ϕ
90°
45°
0 |
|
ω0 |
ωн |
ω |
|
|
ωв |
−45°
−90°
Рис. 52
Явление резонанса в схеме на рис. 53, а с параллельными ветвями, содержащими разнохарактерные реактивные сопротивления, называется резонансом токов.
I1 |
R1 |
L |
I2 |
I E
I
I1
I2 R2 С
E |
б |
|
а
Рис. 53
Ток I1 в ветви с индуктивностью отстает от э.д.с E (см. диаграмму на рис. 53, б) и может быть записан как
I1 = EY1.
Ток I 2 в ветви с емкостью опережает напряжение:
I 2 = EY2.
Ток в неразветвленной части цепи —
I = I1 + I2 = E (Y1 +Y2 ) = E Y .

77
Определим комплексную проводимость Y :
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R1 − jωL |
|
|
R |
+ j |
|
1 |
|
|
|
|
|
|||||
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
ωC |
|
|
|
|||||||||||
Y = |
|
|
+ |
|
|
|
|
|
|
= |
+ |
|
|
2 |
|
|
|
|
= |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
R1 |
+ jωL |
|
|
|
|
|
1 |
|
|
|
|
R12 +ω2 L2 |
|
|
|
|
2 |
|
|
1 |
|
|
|
|
|
||||
|
|
|
|
|
|
R2 − j |
ωC |
|
|
R2 |
+ ω2C2 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
= |
|
R |
|
+ |
|
|
|
R |
|
|
|
|
|
ωL |
|
− |
|
1 ωC |
|
|
|||||||||||
1 |
|
|
|
|
2 |
|
|
− j |
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
R12 +ω2 L2 |
|
2 |
|
1 |
|
|
|
R12 |
+ω2 L2 |
|
|
|
|
2 |
|
1 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
R2 |
+ |
ω2C2 |
|
|
|
|
|
|
R2 + |
ω2C2 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
По определению резонансного режима ток I |
должен совпа- |
||||||||||||||||||||||||||||||
дать по фазе с э.д.с. E . Это будет при условии, что мнимая часть |
|||||||||||||||||||||||||||||||
проводимости Y равна нулю.
Следовательно, условие наступления режима резонанса то-
ков в схеме на рис. 53, а можно записать так: |
|
|||||
|
ωL |
= |
|
1 ωC |
. |
(51) |
|
R12 +ω2L2 |
R22 |
+1 ω2C2 |
|||
|
|
|
|
|||
Изменением одной из величин в (51) при неизменных остальных четырех не всегда может быть достигнут резонанс. Резонанс отсутствует, если значение изменяемой величины, вычисленное по (51), получается мнимым или комплексным. Например, решим (51) относительно ω:
|
|
|
|
|
|
|
L |
|
|
|
R12 |
ωL2 |
|
|
|
|
|||
|
|
|
|
ωLR22 + |
|
|
|
|
= |
|
|
+ |
|
, |
|
|
|
||
|
|
|
ω |
|
2 |
|
|
C |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
ωC |
|
|
|
|
||||||
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω2LR22C2 + L = R12C +ω2L2C, |
|
|
|||||||||||||
|
|
|
|
ω2LC(L −C R22) = L −CR12, |
|
|
|||||||||||||
|
|
1 |
|
L −C R2 |
|
|
1 |
|
|
|
L C − R2 |
|
|
1 ρ2 − R2 |
|||||
ω0 |
= |
|
|
1 |
= |
|
|
|
|
|
|
|
|
1 |
= |
|
|
1 . |
|
|
|
|
|
|
|
|
|
L C − R22 |
|
|
|||||||||
|
|
LC |
|
L −C R22 |
|
|
LC |
|
|
|
LC ρ2 − R22 |
||||||||
То есть резонанс возможен, если R1 и R2 |
оба больше или |
||||||||||||||||||
оба меньше ρ.
Эквивалентная проводимость контура при резонансе равна действительной части комплексной проводимости:
78
|
g = Re[Y ] = |
|
|
|
R1 |
|
|
+ |
|
|
|
|
|
|
|
|
R2 |
|
|
|
|
|
= |
||||||||||||||||
|
R12 +(ω′0 )2 L2 |
|
|
R2 |
+ |
|
1 |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
(ω′ )2 |
C2 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
R1 |
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
R2 |
|
|
|
|
|
|
|
|
= |
|||||||
|
|
2 |
2 1 |
|
|
ρ2 |
− R12 |
|
|
2 |
|
+ |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
R2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
R |
|
|
+ L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ρ |
2 |
|
2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 1 |
|
|
|
|||||||||||||
|
|
|
|
|
|
LC ρ2 |
− R22 |
|
|
|
|
|
|
|
− R1 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C |
|
|
LC |
ρ2 − R22 |
|||||||||||||
|
= |
|
|
|
|
R1 |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
R2 |
|
|
|
|
|
= |
|
|
|||||||||||
|
|
R2 + |
ρ2 |
|
(ρ2 |
− R12 ) |
|
|
R2 |
+ |
|
|
ρ2 |
(ρ2 − R22 ) |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
ρ2 − R2 |
|
|
|
ρ2 − R2 |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
R (ρ2 − R2 ) |
2 |
|
|
|
|
|
− R2 ) |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
R (ρ2 |
|
|
|
|
|
R1 + R2 |
|
|
|
|
||||||||||||||||||||||||
|
= |
1 |
|
|
|
|
|
2 |
+ |
2 |
|
|
|
|
|
|
|
1 |
|
|
|
= |
|
|
. |
||||||||||||||
|
|
ρ4 − R2 R2 |
ρ4 − R2 R2 |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
ρ2 − R R |
|||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
||||||
Потребляемый от источника ток при резонансе минимален и рассчитывается по следующему соотношению:
I p = Eρ(2R+1 + R2 ). R1R2
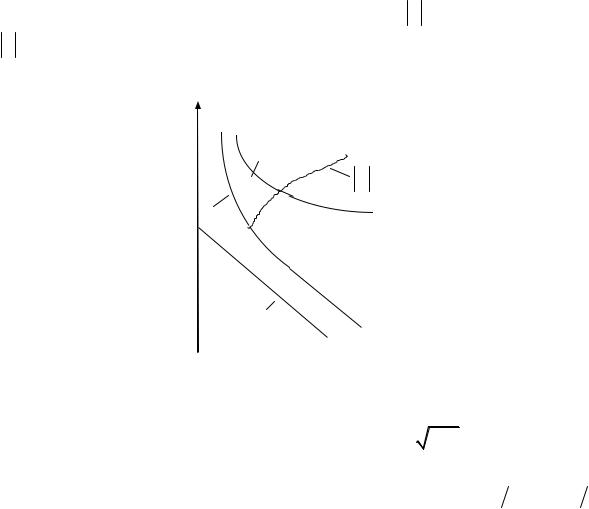
Примерный вид АЧХ для параллельного колебательного контура представлен на рис. 54.
I
I p 2
I p
0 |
ωн |
ωв |
ω |
|
|
|
Рис. 54
Избирательные свойства этого контура, так же как и последовательного, характеризуются полосой пропускания. Границы полосы пропускания ωн и ωв здесь соответствуют увеличению
тока источника по сравнению с резонансным в 2 раз.
79
Если в контуре потери малы, что характерно для радиотехники и электросвязи, то можно считать R1 ≈ 0, R 2 ≈ 0 и резонанс-
ная частота в параллельном контуре будет определяться тем же соотношением, что и в последовательном (см. формулу 44).
Построим зависимость тока от частоты I(ω) в неразветвленной части схемы для идеального случая R1 = R2 = 0.
На рис. 55 показаны частотные характеристики проводимостей ветвей b1 = bL =1 ωL и b2 = −bC = −ωC и входной проводи-
ωL и b2 = −bC = −ωC и входной проводи-
мости цепи b = b1 +b2 =1 ωL −ωC. Ток I = b E , поэтому кривая b = F(ω) в соответствующем масштабе и есть резонансная кривая тока I (ω) .
ωL −ωC. Ток I = b E , поэтому кривая b = F(ω) в соответствующем масштабе и есть резонансная кривая тока I (ω) .
b, I
b1 = bL
b
b
0  ω
ω
b2 = −bC
Рис. 55
При изменении частоты от 0 до ω0 =1 LC эквивалентная
LC эквивалентная
проводимость b > 0, т.е. индуктивная, и изменяется от ∞ до нуля. При ω= ω0 наступает резонанс токов, b = 0, I = 0, I1 = E ω0L = E ρ
и I 2 = ω0CE = E ρ. При возрастании частоты от ω0 до ∞ входная проводимость b<0, т.е. емкостная, и изменяется от нуля до −∞.
ρ. При возрастании частоты от ω0 до ∞ входная проводимость b<0, т.е. емкостная, и изменяется от нуля до −∞.
Пример 17
Для схемы на рис. 50, а дано: R=10 Ом; L= 0,1 мГн; С=100 пФ;
Е=1 В.
Требуется определить величину напряжений на индуктивности и емкости и активную мощность цепи при резонансе.
