
ТОЭ / ТОЭ ТУСУР
.pdf20
Система уравнений (15) собственно и иллюстрирует правило составления уравнений по методу контурных токов.
Смежное сопротивление берется со знаком «минус», если направления контурных токов в этой ветви противоположны, и со знаком «плюс», если совпадают.
В контурные э.д.с. соответствующие э.д.с. входят со знаком «плюс», если их направление совпадает с принятым направлением контурного тока, и со знаком «минус», если направление противоположно.
Если бы в схеме было больше двух контуров, например три, то система уравнений выглядела бы следующим образом:
I11 R11 + I 22 R12 + I33 R13 |
= E11 |
|
|
I11 R21 + I 22 R22 + I33 R23 |
|
|
(15,а) |
= E22 . |
|||
|
|
|
|
I11 R31 + I 22 R32 + I33 R33 = E33 |
|
||
В (15,а) R12 = R21, R13 = R31 , R23 = R32 — смежные сопротивления соответственно первого и второго, первого и третьего, второго и третьего контуров.
В крайних ветвях схемы истинные и контурные токи совпадают, а в смежных определяются как алгебраические суммы контурных токов.
Пример 5
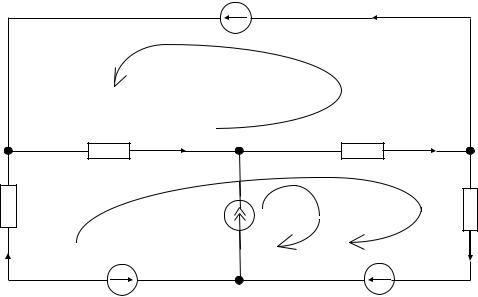
Для схемы на рис. 13 задано: Е1=100 В; Е2=150 В; Е3= 28 В;
J = 2 mА; R2 = 2 кОм; R3 = 4 кОм; R4 = 6 кОм; R5 = 8 кОм.
Требуется определить токи всех ветвей.
В схеме шесть ветвей, четыре узла и один источник тока. По второму закону Кирхгофа для этой схемы необходимо составить два уравнения, столько же и по методу контурных токов.
Наличие источника тока вносит следующие особенности в формирование уравнений: а) ток источника тока, аналогично контурным, необходимо направить только по одному из контуров; б) контурные токи должны направляться по ветвям, не содержащим источник тока.
21
|
I11 |
R4 |
I4 |
E1 I1
R5 I5
R3 |
J |
J |
I22 |
R2 |
|
|
|||
I3 |
E3 |
|
E2 |
I2 |
Рис. 13
В соответствии с выбранными направлениями токов состав-
ляем уравнения, подобные (15) и (15,a): |
|
||||||
I11 |
(R4 + R5)+ I 22 |
(R4 + R5)+ J R5 = E1 |
|
||||
|
|
|
|
|
|
|
; |
I11(R4 + R5)+ I 22 (R2 + R3 + R4 + R5)+ J (R2 + R5) = E2 − E3 |
|||||||
14 |
I11 |
+14 |
I 22 +16 10 |
−3 |
|
|
|
|
= 0,1 |
|
|||||
14 |
I11 |
+ 20 |
I 22 + |
|
|
; |
|
0,02 = 0,122 |
|
||||||
I11 = 3 mA; I 22 = 3 mA.
По контурным токам определяем истинные токи ветвей:
I1 = I11 = 3 mA; I 2 = I 22 + J = 3 + 2 = 5 mA;
I3 = I 22 = 3 mA; I 4 = I11 + I 22 = 3 + 3 = 6 mA;
I5 = I11 + I 22 + J = 3 + 3 + 2 = 8 mA.
2.5 Метод узловых потенциалов
Ток в любой ветви схемы может быть определен с помощью обобщенного закона Ома по формуле (7). Но чтобы применить закон Ома, нужно знать потенциалы узлов. Метод, в котором за неизвестные принимают потенциалы узлов, называется методом узловых потенциалов.
22
Причем если один узел заземлить (принять его потенциал равным нулю), то число неизвестных сокращается на единицу. Метод целесообразно применять для сложных схем с небольшим числом узлов.
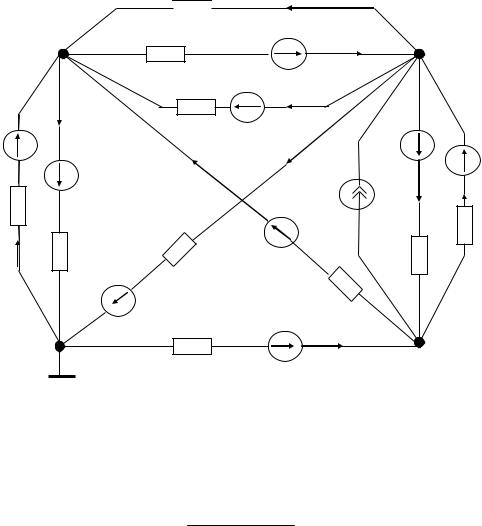
Для обоснования метода используем схему на рис. 14, содержащую четыре узла и 11 ветвей. Узел 4 заземлим.
|
R3 |
|
I3 |
|
|
||
|
|
|
|
1 |
R4 |
|
E4 |
I4 |
2 |
|
R5 |
E5 |
I5 |
|
|
E1 |
I2 |
I7 |
I6 |
E10 |
|
|
E2 |
|
E11 |
||
|
|
|
J9 |
||
|
|
|
|
|
|
R1 |
|
|
E7 |
I10 |
I11 |
I1 |
R2 |
R6 |
R7 |
R10 |
R11 |
|
|||||
4 |
E6 |
R8 |
E8 I8 |
3 |
|
|
|
|
|
Рис. 14
Составим уравнение по первому закону Кирхгофа для узла 1:
I1 − I 2 + I3 − I 4 + I5 + I 7 = 0. |
(16) |
На основании формулы (7) можно записать:
I1 = (ϕ4 −ϕ1)+ E1 = [(ϕ4 −ϕ1)+ E1]g1;
R1
I 2 = [(ϕ1 −ϕ4)+ E2]g2;
I3 = (ϕ2 −ϕ1)g3;
I 4 = [(ϕ1 −ϕ2)+ E4]g4;
I5 = [(ϕ2 −ϕ1)+ E5]g5;
I 7 = [(ϕ3 −ϕ1)+ E7]g7.
23
Подставим последние соотношения в (16):
[(ϕ4 −ϕ1)+ E1]g1 −[(ϕ1 −ϕ4)+ E2]g2 +[(ϕ2 −ϕ1)+ 0]g3 −
−[(ϕ1 −ϕ2)+ E4]g4 +[(ϕ2 −ϕ1)+ E5]g5 +[(ϕ3 −ϕ1)+ E7]g7 = 0.
Перепишим уравнение (17) следующим образом:
ϕ1G11 +ϕ2 G12 + ϕ3 G13 = I11.
Здесь обозначено:
G11 = g1 + g 2 + g3 + g 4 + g5 + g7; G12 = −(g3 + g 4 + g5);
G13 = −g7;
I11 = E1g1 + E5g5 + E7 g7 − E2 g 2 − E4 g 4.
(17)
(18)
Проанализируем структуру уравнения (18).
Множителем при ϕ1 является сумма проводимостей всех
ветвей, сходящихся в узле 1.
G12 равняется сумме проводимостей ветвей, соединяющих узлы 1 и 2, взятой со знаком «минус», аналогично и G13 .
Ток I11 называется узловым током (первого узла). Это расчетная величина, равная алгебраической сумме токов, полученных от деления э.д.с. ветвей, подходящих к узлу 1, на сопротивления данных ветвей (со знаком «плюс» токи тех ветвей, э.д.с. которых направлены к узлу 1).
Подобные уравнения могут быть составлены и для остальных узлов. Например, для произвольной схемы с n узлами:
ϕ1G11 +ϕ2 G12 + ... + ϕn−1G1,n−1 = I11 |
|
|
|
|
|
ϕ1G21 +ϕ2 G22 +... +ϕn−1G2,n−1 = I 22 |
(19) |
|
............................................ |
. |
|
|
|
|
ϕ1Gn−1,1 +... +ϕn−1Gn−1,n−1 = I n−1,n−1 |
|
|
|
|
|
Здесь Gkk — сумма проводимостей ветвей, сходящихся в узле k; Gkm — сумма проводимостей ветвей, объединяющих узлы k и m, взятая со знаком «минус»; Ikk — узловой ток узла k (если к узлу k подтекает ток и от источника тока, то он должен добавить-
ся к Ikk со знаком «плюс», а если вытекает — то со знаком «минус»).
24
Если между какими-либо двумя узлами нет ветвей, то соответствующая проводимость равна нулю.
После определения узловых потенциалов по обобщенному закону Ома определяются токи в ветвях.
Пример 6
Для схемы на рис. 14 задано: E1= E6=10 В; E2 = 6 В; E4=20 В;
E5=30 В; E7=14 В; E8=8 В; E10=12 В; E11=7 В; R1=1 Ом; R2= R7= =R8= R11=2 Ом; R3=5 Ом; R4= R5=10 Ом; R6= R10=4 Ом; J9=1,5 А.
Требуется методом узловых потенциалов определить токи в ветвях.
Согласно (19) записываем систему уравнений:
ϕ1G11 +ϕ2 G12 +ϕ3 G13 = I11
ϕ1G21 +ϕ2 G22 +ϕ3 G23 = I 22 .
ϕ1G31 +ϕ2 G32 +ϕ3 G33 = I33
Подсчитываем проводимости:
G11 |
= |
1 |
+ |
1 |
+ |
1 |
+ |
1 |
+ |
1 |
+ |
1 |
= |
|
|
|
|
|
|
||||||||
|
|
R1 R2 R3 R4 R5 R7 |
|||||||||||
|
=1+0,5 +0,2 +0,1+0,1+0,5 = 2,4 Cм; |
||||||||||||
G22 |
= |
|
1 |
+ |
1 |
|
+ |
1 |
|
+ |
1 |
+ |
1 |
+ |
1 |
= |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
R3 |
|
|
R4 |
|
|
|
R5 |
|
|
R6 |
|
R10 R11 |
|
|
|
||||||||||||||||||||
= 0,2 +0,1+0,1+0,25 +0,25 +0,5 =1,4 См; |
|
|
||||||||||||||||||||||||||||||||||||
G33 |
= |
1 |
+ |
1 |
|
+ |
|
|
1 |
|
|
|
+ |
|
|
1 |
|
= 0,5 +0,5 +0,25 +0,5 =1,75 Cм; |
||||||||||||||||||||
|
|
|
|
R10 |
R11 |
|||||||||||||||||||||||||||||||||
|
|
|
R7 |
|
|
R8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|||||||||||||
G12 |
= G21 |
= − |
|
|
|
|
+ |
|
|
|
|
|
|
|
+ |
|
|
|
= −0,2 −0,1 |
−0,1 |
= −0,4 |
См; |
||||||||||||||||
R3 |
|
R4 |
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R5 |
|
|
|
|||||||||||||||||||
G13 |
= G31 |
= − |
1 |
= −0,5 См; |
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
R7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
G23 |
= G32 |
= − |
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|
= −0,25 −0,5 = −0,75 См |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
R10 |
|
R11 |
|
|
|
|
|
|
|
|
|
||||||||||||||||
(при расчете G22 , G33 , G23 учтено, что проводимость ветви с источником тока J9 равна нулю).
25
Определяем узловые токи:
I11 |
= E1 − E2 − E4 + E5 + E7 =10 − |
6 |
− |
20 |
+ |
|
30 |
+ |
|
14 |
|
=15 А; |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
R1 |
R2 |
R4 |
R5 |
R7 |
|
|
2 10 10 |
2 |
|
|
|
|
||||||||||||||||||||
I22 |
= E4 − E5 − E6 |
− E10 + E11 |
+ J9 |
= |
20 |
− |
30 |
− |
10 |
− |
12 |
+ |
7 |
+1,5 = −1,5 А; |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
R4 |
R5 |
R6 |
R10 |
R11 |
|
|
10 10 4 |
4 2 |
||||||||||||||||||||||||
I33 |
= − E7 |
+ E8 |
+ E10 − E11 − J 9 |
= − |
14 |
+ |
8 |
|
+ |
12 |
− |
7 |
−1,5 = −5 А. |
||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||
|
R7 |
R8 |
R10 |
R11 |
|
|
2 2 |
|
4 2 |
|
|
|
|
|
|||||||||||||||||||
Подставляем полученные данные в исходную систему уравнений:
2,4ϕ1 − |
0,4ϕ2 −0,5ϕ3 |
=15 |
|
||
−0,4ϕ |
+1,4ϕ |
|
−0,75 |
|
|
2 |
ϕ = −1,5 . |
||||
1 |
|
|
3 |
|
|
− ϕ − ϕ + ϕ = −
0,5 1 0,75 2 1,75 3 5
Решим полученную систему с помощью определителей:
|
2,4 |
−0,4 |
−0,5 |
|
|
|
|
||||||||||
|
|
||||||||||||||||
= |
−0,4 |
1,4 |
−0,75 |
|
= 3,6; |
||||||||||||
|
−0,5 |
−0,75 |
1,75 |
|
|
|
|
|
|
|
|
||||||
|
|
|
15 |
−0,4 |
−0,5 |
|
|
||||||||||
|
|
|
|||||||||||||||
1 = |
|
|
−1,5 |
1,4 |
−0,75 |
|
= 21,7; |
||||||||||
|
|
|
|
|
|
|
−5 |
−0,75 |
1,75 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2,4 |
15 |
−0,5 |
|
|
||||||||
|
|
|
|||||||||||||||
2 = |
|
|
|
−0,4 |
−1,5 |
−0,75 |
|
= 0,2; |
|||||||||
|
|
|
|
|
|
|
−0,5 |
−5 |
1,75 |
|
|
|
|
|
|
|
|
|
|
|
2,4 |
0,4 |
15 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||||||||
3 = |
|
−0,4 |
1,4 |
−1,5 |
|
= −4; |
|||||||||||
|
|
|
|
|
|
|
−0,5 |
−0,75 |
−5 |
|
|
||||||
ϕ1 = |
|
|
|
|
|
|
1 = 21,7 3,6 = 6,03 B; |
||||||||||
ϕ2 = |
2 |
= 0,2 3,6 = 0,06 B; |
|||||||||||||||
ϕ3 = |
3 |
= −4 3,6 = −1,11B. |
|||||||||||||||
26
Рассчитаем токи в ветвях, применив формулу (7):
I1 = (−ϕ1 + E1) R1 = (−6,03 +10)
R1 = (−6,03 +10) 1 = 3,97 A;
1 = 3,97 A;
I3 = (ϕ2 −ϕ1) R3 = −5,97
R3 = −5,97 5 = −1,194 A;
5 = −1,194 A;
I8 = (−ϕ3 + E8) R8 = (1,11+8)
R8 = (1,11+8) 2 = 4,555 A;
2 = 4,555 A;
I11 = [(ϕ3 −ϕ2)+ E11] R11 = (−1,11−0,06 +7)
R11 = (−1,11−0,06 +7) 2 = 2,915 A
2 = 2,915 A
и так далее.
Сделаем проверку по второму закону Кирхгофа для внешнего контура схемы (выберем направление обхода контура по часовой стрелке).
Сумма падений напряжений:
I1 R1 − I3 R3 − I11 R11 − I8 R8 = 3,97 1+1,194 5 −2,915 2 −4,555 2 = −5В. Сумма э.д.с.: E1 − E11 − E8 =10 −7 −8 = −5 B.
Второй закон Кирхгофа для выбранного контура выполняется, что и подтверждает правильность расчетов.
2.6 Метод двух узлов
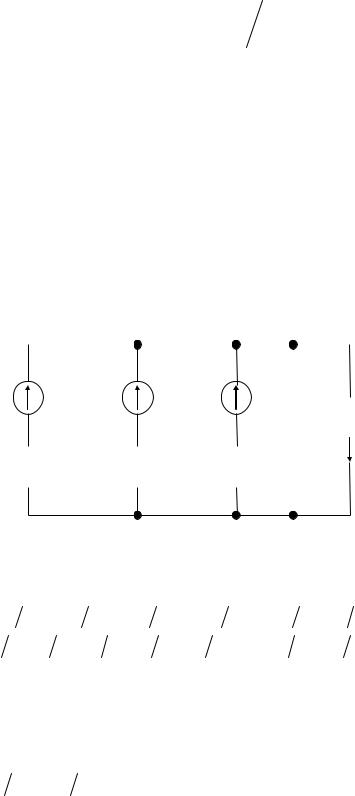
Метод двух узлов наиболее целесообразен для расчета схем с двумя узлами и непосредственно вытекает из метода узловых потенциалов. Для схемы с n параллельными ветвями на рис. 15 согласно формуле (18) можно записать:
ϕa Gaa = I aa.
а
|
|
R1 |
|
|
|
|
R2 |
|
|
|
|
Rn |
||
|
|
|
|
|
|
|
|
|||||||
|
|
Е1 |
|
|
|
|
Е2 |
|
|
En |
||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||
|
I1 |
b |
|
I2 |
|
|
In |
|||||||
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 15
27
С учетом принятых на рис. 15 обозначений последнее соотношение перепишем для частного случая отсутствия источников тока:
n |
n |
|
|
ϕa ∑ gk = ∑(Ek gk ); |
|
||
k =1 |
k =1 |
|
|
|
n |
n |
|
U ab = |
∑(Ek gk ) |
∑gk. |
(20) |
|
k =1 |
k =1 |
|
После определения U ab |
находятся токи в ветвях по уже из- |
||
вестной формуле: |
|
|
|
I n = (En −U ab)gn . |
(21) |
||
Пример 7
Три генератора с э.д.с. Е1= 48 В; Е2= Е3= 45 В и внутренними сопротивлениями r1=1,2 Ом, r2=1 Ом, r3=1,5 Ом работают параллельно на общую нагрузку R=4,2 Ом, как показано на рис. 16.
Требуется определить напряжение на нагрузке Uаb, токи нагрузки и генераторов.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
|
|||
|
|
|
|
Е1 |
|
|
|
|
Е2 |
|
|
|
|
Е3 |
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
r1 |
|
|
|
|
r2 |
|
|
|
|
r3 |
|
|
|
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
Рис. 16 |
|
|
|
|
|
|
||||||
По формуле (20) определяем напряжение на нагрузке: |
|
||||||||||||||||||||
U ab = |
E1 r1 + E2 |
r2 + E3 |
r3 |
= |
|
48 1,2 + 45 1+ 45 1,5 |
= 42 |
В. |
|||||||||||||
1 r1 |
+1 r2 |
+1 r3 +1 R |
1 1,2 +1+1 1,5 +1 4,2 |
||||||||||||||||||
|
|
|
|
||||||||||||||||||
По формуле (21) вычисляем искомые токи:
I1 = (E1 −U ab) r1 = (48 −42)
r1 = (48 −42) 1,2 = 5 А;
1,2 = 5 А;
I 2 = (E2 −U ab) r2 = (45 −42)
r2 = (45 −42) 1 = 3 А;
1 = 3 А;
I3 = (E2 −U ab) r3 = (45 −42)
r3 = (45 −42) 1,5 = 2 А;
1,5 = 2 А;
I =U ab R = 42 4,2 =10 А.
28
2.7 Метод наложения. Преобразование схем
Ток в любой ветви линейной электрической цепи можно рассматривать как алгебраическую сумму частичных токов, вызываемых в этой ветви каждым из источников в отдельности. Это положение называется принципом наложения или принципом суперпозиции, а основанный на этом положении метод — методом наложения. Для расчета этим методом цепи необходимо:
1) произвольнорасставитьнаправлениядействительныхтоков;
2) составить частичные схемы замещения, оставив в каждой по одному источнику. Внутренние же сопротивления исключенных источников должны оставаться во всех частичных схемах;
3) рассчитав каждую схему, найти частичные токи во всех ветвях;
4) определить действительные токи как алгебраическую сумму соответствующих частичных токов.
Примечание: методом наложения нельзя пользоваться для подсчета выделяемых в сопротивлениях мощностей, т.к. мощность пропорциональна квадрату тока.
При расчете частичных схем возникает необходимость определения эквивалентного сопротивления отдельных участков схем и токораспределения в ветвях схемы.
Наиболее часто используется последовательное либо параллельное соединение резисторов и их комбинации — смешанное соединение.
Для определения эквивалентного параметра при последовательном соединении суммируются сопротивления, а при параллельном — проводимости. В частном случае параллельного соединения двух резисторов, как показано на рис. 17, получим эк-
вивалентное сопротивление: |
|
|
|
|
|
|
|
|
(R1 |
+ R2) |
|||||
1 |
= g |
|
= |
1 |
+ |
1 |
= |
||||||||
|
|
|
э |
|
|
|
|
|
|
, |
|||||
|
R |
э |
R |
R |
|
R R |
|||||||||
|
|
|
|
2 |
|
|
2 |
||||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
1 |
|
|
|
|
|
1 |
||||
|
|
|
|
Rэ = |
|
R1R2 |
. |
|
|
(22) |
|||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
R1 + R2 |
|
|
|
|||||

29
I1 R1
I
I2 R2
Рис. 17
При параллельном соединении нагрузок токи в них распределяются прямо пропорционально проводимостям. Поэтому для двух параллельных нагрузок токи в каждой из них определяются через ток I в неразветвленной части цепи (см. рис. 16) следующими соотношениями:
|
|
|
|
g1 |
1 |
R1 |
|
R2 |
|
|
|||
I1 |
= I |
|
|
|
|
= I |
|
|
= I |
|
|
; |
|
g1 |
+ g 2 |
|
+1 R2 |
|
+ R2 |
|
|||||||
|
|
1 R1 |
|
R1 |
|
(23) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I 2 = I |
|
R1 |
. |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||
R1 + R2 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||
При последовательном соединении нагрузок напряжения на них прямо пропорциональны сопротивлениям. Следовательно, для схемы на рис. 18
I |
R1 |
E |
U2 |
R2 |
Рис. 18 |
|
|
|
U2 |
= I R2 |
= |
|
E |
R2 |
= E k, |
|
|
|
R1 |
+ R2 |
|||||
|
|
|
|
|
|
|
|
||
где k = |
|
R2 |
— коэффициент передачи. |
|
|||||
R1 |
+ R2 |
|
|||||||
|
|
|
|
|
|
|
|
||
