
ТОЭ / ТОЭ ТУСУР
.pdf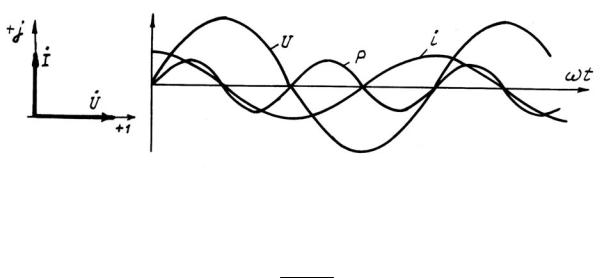
50
а |
б |
Рис. 34
Мгновенная мощность
p = ui = U mI m sin 2ωt. 2
За первую четверть периода конденсатор потребляет от источника энергию (мгновенная мощность положительна, см. рис. 34, б), которая идет на создание электрического поля в нем. Во вторую четверть периода напряжение на конденсаторе уменьшается от максимума до нуля и запасенная в электрическом поле энергия отдается источнику (мгновенная мощность отрицательна). Далее процессы повторяются.
3.4 Основы символического метода
Пусть есть некоторый вектор A = Ae jϕ. Каков будет результат от умножения этого вектора на j и на −j ?
Представим векторы j и −j в показательной форме: j =1e j90°;
− j =1e− j90°.
Произведем умножение:
Aj =Aejϕej90 =Aej(ϕ+90 );
A(−j) = Ae jϕe−j90 = Ae j(ϕ−90 ).
По модулю результирующий вектор не меняется. Умножение A на j поворачивает исходный вектор на 90° в сторону опережения, т.е. против часовой стрелки, а умножение A на −j поворачивает исходный вектор на 90° в сторону отставания, т.е. по часовой стрелке. Это и показано на рис. 35.

51
+j
jA A
+1
−jA
Рис. 35
С учетом изложенного перейдем к сущности символического метода расчета цепей синусоидального тока. Он заключается в переходе от дифференциальных уравнений, составленных для мгновенных значений величин, к алгебраическим уравнениям, составленным относительно комплексов тока и э.д.с.
Мгновенные значения тока i заменяют комплексной амплитудой тока I m ;
мгновенное значение напряжения на резисторе uR, равное Ri, заменяют комплексом RI m ;
|
мгновенное |
значение |
напряжения |
на |
индуктивности |
||
uL = Ldi dt |
заменяют комплексом jI mωL , |
опережающим ток на |
|||||
90°; |
мгновенное |
значение |
напряжения |
на |
конденсаторе |
||
|
|||||||
uC = |
1 |
∫idt |
заменяют комплексом − jI m ωC , отстающим от тока |
||||
|
|||||||
|
C |
|
|
|
|
|
|
на 90°; |
|
|
|
|
|
||
мгновенное значение э.д.с. е заменяют комплексом Em .
Например, для схемы на рис. 36 уравнение для мгновенных значений можно записать так:
e = uR +uL +uC, или e = iR + Ldi |
dt + |
1 |
∫idt. |
|||
C |
||||||
Запишем его в комплексной форме: |
|
|
|
|||
|
|
|
|
|||
Em = I mR + jI mωL − jI m ωC = I m(R + jωL − j ωC). |
||||||
Следовательно, для схемы (см. рис. 36) |
|
|||||
I m = |
Em |
|
. |
|
|
|
|
|
|
|
|||
|
R + jωL − j ωC |
|
||||

52
R L C
 I
I
~  E
E
Рис. 36
Это уравнение позволяет найти комплексную амплитуду тока I m через комплексную амплитуду э.д.с. Em и сопротивления
цепи R, ωL и 1 ωC .
ωC .
Метод называют символическим потому, что ток и каждое напряжение заменяются своими комплексными изображениями, или символами. Так, jI mωL есть изображение, или символ, на-
пряжения на индуктивности uL = Ldi dt и т.д.
dt и т.д.
Комплексная величина R + jωL − j ωC имеет размерность сопротивления, называется комплексным сопротивлением и
ωC имеет размерность сопротивления, называется комплексным сопротивлением и
обозначается через Z. Как и всякий комплекс, Z можно записать в показательной форме:
Z = ze jϕ = R + jωL − j ωC .
ωC .
Модуль комплексного сопротивления принято обозначать через z. Точку над Z не ставят, потому что принято ставить ее только над такими комплексными величинами, которые отображают синусоидальные функции времени.
Исходное уравнение для рассматриваемой схемы можно за-
писать так: Em = I mZ. Поделив обе его части на |
2 , получим |
уравнение для комплексов действующих значений: |
|
I =E Z. |
(33) |
Уравнение (33) представляет собой закон Ома для цепи си-
нусоидального тока.
Вобщем случае Z имеет некоторую действительную часть R
инекоторую мнимую часть jX:
Z = R + jX ,
где R — активное сопротивление, X — реактивное.
53
Для схемы на рис. 36 реактивное сопротивление
X = ωL −1/ ωC.
Величина Y, обратная комплексному сопротивлению, назы-
вается комплексной проводимостью.
Y = 1 = g − jb = ye− jϕ. Z
Единица комплексной проводимости — См (Ом–1). Действительную часть ее обозначают через g, а мнимую — через b. Так как
|
1 |
= |
|
1 |
|
= |
R − jX |
= |
|
R |
|
− j |
X |
= g − jb, |
||||||
|
|
|
|
|
R2 + X 2 |
|
R2 + |
X 2 |
R2 + X 2 |
|||||||||||
|
Z R + jX |
|
|
|
|
|
|
|
||||||||||||
то |
|
|
R |
|
|
|
|
|
|
X |
|
|
|
|
|
|||||
|
|
g = |
|
|
|
|
; |
b = |
|
|
; y = |
g 2 +b2. |
(34) |
|||||||
|
|
|
R2 + |
X 2 |
R2 |
+ X 2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Если Х положительно, то и b положительно. При Х отрицательном b также отрицательно.
При использовании комплексной проводимости закон Ома (33) запишется так:
I =UY =Ug − jUb = I a + I р,
где I a — активная составляющая тока; I р — реактивная составляющая тока;
U — напряжение на участке цепи, сопротивление которого равно Z.
Модуль комплексного сопротивления
z = R2 + X 2.
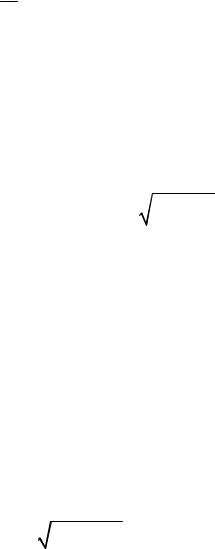
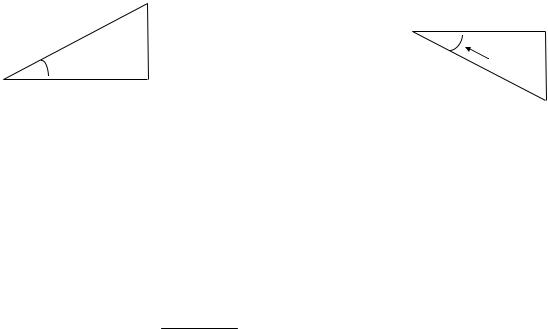
Графическая интерпретация этого выражения называется
треугольником сопротивлений и приводится на рис. 37, а
Аналогично применяется и понятие треугольника проводимостей. Такой треугольник показан на рис. 37, б.
Расчет любой цепи переменного тока связан с комплексными числами. Поэтому нужно иметь в виду следующее.
54
z |
tgϕ = |
X |
= |
b |
. |
g |
|
|
|
|
|||||
|
|
R g |
|
|
|||
ϕ |
X |
ϕ |
b |
||||
|
|
|
|
|
|
y |
|
R |
|
|
|
|
|
|
|
а |
Рис. 37 |
б |
|
||||
Сложение двух и большего числа комплексов удобнее производить, используя алгебраическую форму записи:
(a1 + jb1) +(a2 + jb2) +(a3 + jb3) = (a1 + a2 + a3) + j(b1 +b2 +b3).
Деление и умножение комплексных чисел удобнее всего производить, пользуясь показательной формой записи:
C 1e jϕ1 = C 1 e j ( ϕ1 − ϕ2 ). |
||
C 2 e |
jϕ2 |
C 2 |
|
||
По первому закону Кирхгофа алгебраическая сумма мгновенных значений токов, сходящихся в любом узле схемы, равна нулю. Заменив каждый ток его комплексным изображением, по-
лучим выражение первого закона Кирхгофа в символической форме:
∑ I = 0. |
(35) |
Аналогично этому записывается для любого замкнутого контура и второй закон Кирхгофа в символической форме:
∑ IZ = ∑ E. |
(36) |
Для расчета цепей постоянного тока разработаны методы на основе первого и второго законов Кирхгофа, с помощью которых вести расчет проще, чем решать систему уравнений, составленных непосредственно по законам Кирхгофа. Но законы Кирхгофа применимы и для синусоидальных цепей переменного тока. Поэтому все рассмотренные методы расчета цепей постоянного тока применимы и здесь. Нужно лишь вместо постоянного тока I ис-
пользовать комплекс тока I , вместо проводимости g — комплексную проводимость Y, вместо сопротивления R — комплексное сопротивление Z и вместо постоянной э.д.с. Е — комплексную э.д.с. E .
55
Ток и напряжения на различных участках цепи синусоидального тока, как правило, по фазе не совпадают. Наглядное представление о фазовом расположении различных векторов дает векторная диаграмма токов и напряжений, вследствие чего с помощью такой диаграммы можно контролировать правильность производимых аналитических расчетов. Рассмотрим это на примерах.
Пример 11 |
|
|
|
|
|
|
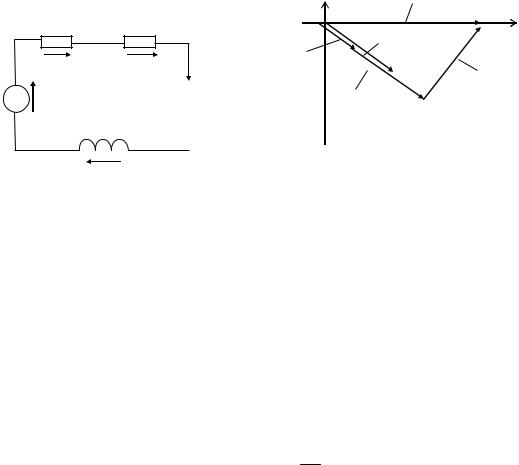
В схеме на рис. 38, а e = 141sin ωt |
В; R1=3 Ом; R2=2 Ом; |
|||||
L=0,00955 Гн; ω=314 с–1. Требуется определить ток и напряжения |
||||||
на элементах цепи. |
|
|
|
|
|
|
|
|
|
|
+j |
|
E |
R1 |
R2 |
|
|
|
|
|
|
|
|
|
|
I |
+1 |
UR |
UR |
|
I |
UR |
|
U L |
|
|
|||||
1 |
2 |
|
|
2 |
|
|
~ E |
|
|
|
UR |
|
|
L |
|
|
|
|
||
|
|
|
|
1 |
|
|
UL |
|
|
|
|
|
б |
|
|
|
|
|
||
а |
|
|
|
|
|
|
Рис. 38
Замечание. Направления токов, э.д.с. и напряжений на переменном токе изменяются с каждым полупериодом. Поэтому на схемах направления указанных величин обозначаются лишь для одного из полупериодов.
Р е ш е н и е.
Запишем уравнение для мгновенных значений:
i(R1 + R2) + L di = e. dt
Перейдем от него к уравнению в комплексах:
I (R1 + R 2) + jωLI = E, или IZ = E,
где Z = R1 + R2 + jωL = 3 + 2 + j314 0,00955 = 5 + j3 =

56
= 52 +32 e jarctg3 5 = 5,83e j31° Ом.
5 = 5,83e j31° Ом.
Комплекс действующего значения э.д.с. E =141 2 =100 В.
2 =100 В.
Ток в цепи |
j31° =17,2 − j31°A. |
|
|
I = E Z =100 5,83 |
|
|
e |
e |
Напряжение на элементах R1, R2, L : |
||
U R1 |
= I R1 = 51,6e− j31°В. |
|
U R2 |
= I R2 = 34,4e− j31°В. |
|
U L |
= jωLI = e j90° 3 17,2e− j31° = 51,6e j59°В. |
|
Если бы в рассматриваемой схеме к элементам подключили вольтметры (эффективного значения), то их показания соответствовали бы модулям найденных комплексов напряжений
(U R1 = 51,6В; U R2 = 34,4В; U L = 51,6В;).
Векторная диаграмма изображена на рис. 38, б. Вектор E , имеющий нулевую начальную фазу, направлен по оси +1. Вектор I отстает от него на 31°. Вектор напряжения на индуктивности U L опережает вектор тока на 90°. Сумма векторов падений на-
пряжения на элементах схемы равна э.д.с. E .
Пример 12
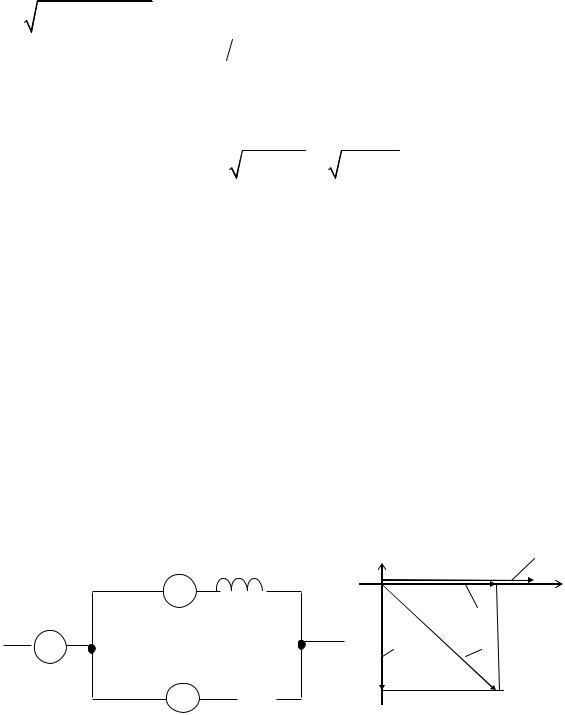
В схеме на рис. 39, а R=4 Ом; ω =105 c−1 . При Е = 10 мВ по цепи протекал ток I = 2 мА (здесь E и I не комплексы, а модули). Требуется определить величину емкости конденсатора.
R |
C |
+j |
I |
U R |
+1
~ E |
I |
E |
U C |
|
а |
б |
|
|
|
Рис. 39 |
|
57
Комплексное сопротивление цепи Z = R − j ωC, его модуль z = R2 +(1
ωC, его модуль z = R2 +(1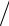 ωC)2 .
ωC)2 .
По закону Ома I = E |
z. Отсюда |
||||
z = |
E |
= |
10−2 |
= 5 Ом. |
|
|
2 10−3 |
||||
|
I |
|
|
|
|
Следовательно,
X С =1 ωС = z2 − R2 = 52 −42 = 3 Ом;
ωС = z2 − R2 = 52 −42 = 3 Ом;
C = 1 ωX C = 1
ωX C = 1 105 3 = 3, 33 мкФ.
105 3 = 3, 33 мкФ.
Векторная диаграмма изображена на рис. 39, б. Начальные фазы E и I по условию заданы не были. Поэтому один из указанных векторов, а именно I , направлен по оси +1. Расположение остальных векторов определилось относительно вектора I . Если бы по оси +1 был направлен вектор E , то вся диаграмма повернулась бы на соответствующий угол против часовой стрелки. Но от поворота взаимное расположение всех векторов не изменилось бы.
Пример 13
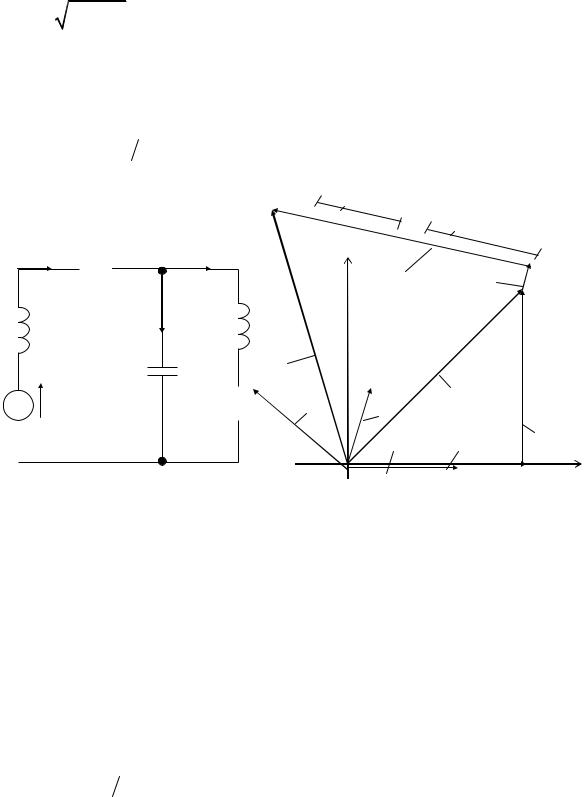
На участке разветвленной цепи, как показано на рис. 40, а, активное сопротивление численно равно индуктивному. Амперметр А2 показывает 5 А. Что покажет А3 ?
|
|
|
|
|
|
U ab |
|
А1 |
|
L |
+j |
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I 2 |
А3 |
a |
|
|
b |
I1 |
I 3 |
|
А2 |
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
|
Рис. 40 |
б |
|
|
|
|
|
|
||
Построим векторную диаграмму, как показано на рис. 40, б. |
||||||
Величина вектора U ab |
взята произвольно, т.к. на решение задачи |
|||||
не влияет. Ток I1 отстает от тока I2 |
на 90° и равен ему по величи- |
|||||
58
не. Ток неразветвленной части схемы I 3 = I 2 + I1. Модуль тока I 3 равен 52 +52 = 7,05 А. Это значение и покажет амперметр А3 .
Пример 14
Построить векторную диаграмму токов и напряжений для
схемы на рис. 41, а, если R1 = 10 |
Ом; |
R3 = 2,5 Ом; ωL1 =10 Ом; |
||||||||||||||||||||||
ωL3 = 20 Ом; 1 ωC =14,1 Ом; I1 = 1 A. |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 В |
|
|
1 А |
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I 3 |
|
R3 |
|
|
|
|
|
I1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+j |
U L3 |
|
U R3 |
|
||
|
L3 |
|
|
|
|
|
|
|
I 2 |
|
|
|
|
L1 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
~ E |
|
|
|
|
|
|
|
|
C |
|
|
|
R1 |
I 2 |
|
I 3 |
|
|
U ab |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I1 |
|
|
U R1 |
U L1 |
|
|
|
|
|
а |
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 41 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Выберем положительные направления токов в соответствии |
|||||||||||||||||||||||
с рисунком. Ток I1 направим по оси +1, т.е. I1 = I1e j0. |
|
|||||||||||||||||||||||
|
U R1 |
|
= R |
1 |
=10e j0 В (совпадает с током |
I |
1 |
). |
|
|||||||||||||||
|
|
|
1I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
U L1 |
= jωL |
|
|
=10e j90 |
|
В (опережает ток |
I |
1 |
на 90°). |
|
|||||||||||||
|
|
|
|
1I1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
U ab =U R1 |
+U L1 |
=10e j0 +10e j90 |
=10 + j10 =14,1e j45 |
В. |
|||||||||||||||||||
|
|
|
|
U ab |
|
|
|
14,1 |
j45 |
|
|
|
|
|
|
|
||||||||
|
I 2 = |
|
|
= |
|
|
e |
|
|
=1e j135 |
А (опережает U ab |
на 90°). |
||||||||||||
|
|
− j ωC |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
14,1e |
− j90 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
I 3 = I1 + I 2 =1+1e j135 |
=1+ j0,7 −0,7 = 0,3 + j0,7 = 0,76e j67 А. |
||||||||||||||||||||||
|
U R3 |
= R3I 3 = 2,5 0,76e j67 =1,9e j67 В(совпадаетстоком I 3 ). |
||||||||||||||||||||||

59
U L3 = jωL3I 3 = 20 0,76e j67 e j90 =15,2e j157 В (опережает ток
I 3 на 90°).
E =U L3 +U R3 +U ab.
U L3 |
=15,2e j157 =15,2cos157 + j15,2sin157 = (−14 + j5,93) В. |
U R3 |
=1,9e j67 =1,9cos67 + j1,9sin 67 = (0,74 + j1,75) В. |
E= (−14 +0,74 +10) + j(5,93 +1,75 +10) = −3, 26 + j17,68 =
=3, 262 +17, 682 e jϕ = 18e jϕ В.
Анализируя величины и знаки действительной и мнимой частей комплексной величины, можно видеть, что вектор E расположен во второй четверти комплексной плоскости. Значит, с учетом периодичности функции аргтангенса, угол ϕ следует вычислять по формуле:
ϕ = π−arctg(17,68 3, 26) =180 −80 =100 .
3, 26) =180 −80 =100 .
Следовательно, E =18e j100 В.
Векторная диаграмма с учетом принятого масштаба построена на рис. 41, б.
3.5 Активная, реактивная и полная мощности
Мощность переменного тока — величина, периодически изменяющаяся. Ее мгновенное значение p = ui.
Пусть ток отстает по фазе от напряжения на угол ϕ, т.е. u =U m sin ωt; i = I m sin(ωt −ϕ). Тогда мгновенное значение мощности
p = ui =U mI m sin ωt sin(ωt −ϕ).
Но
sin α sinβ = 1 cos(α −β) − 1 cos(α +β).
2 |
2 |
|||
Тогда |
|
|
||
p = |
2U 2I |
cos ϕ− |
2U 2I |
cos(2ωt −ϕ) = |
|
2 |
|||
2 |
|
|
||
=UI cosϕ−UI cos(2ωt −ϕ).
