
ТОЭ / ТОЭ ТУСУР
.pdf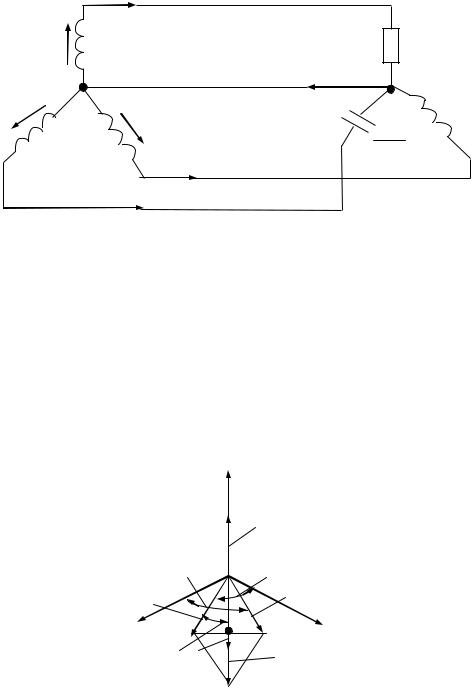
100
АI A
E A |
|
R |
|
0 |
|
I 0 0′ |
|
EC |
|
ωL |
|
E B |
I B |
1 |
|
ωС |
|||
|
|
СВ
I C
Рис. 75
Для решения построим векторную диаграмму, которая показана на рис. 76. Токи всех фаз по модулю равны 127 6,35 = 20 А.
6,35 = 20 А.
Ток I A совпадает по фазе с E A , ток I B отстает от E B на 90°, ток I C опережает EC на 90°.
E A
|
|
|
I А |
|
90° |
0 |
90° |
I B |
|
|
I C |
EC |
m |
n |
E B |
|
30° I 0 |
|
I B + I C |
Рис. 76
Из векторной диаграммы модуль суммы векторов I B и I C —
I В + I С = 0n 2 = 0m cos30 2 = 20cos30 2 = 34,64 А.
Модуль тока I 0 —
I 0 = (I В + I С) − I А = 34,64 −20 =14,64 А.
101
Ток I 0 направлен в противоположную сторону относитель-
но I А и E A , т.е. I 0 = 1 4, 6 4 e − j1 8 0 А.
|
|
Решим задачу символическим методом: |
|
|||||||||||||||||||
I A = |
E A |
= |
127 |
|
= 20 A; |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
R |
6,35 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
I B |
= |
E B |
|
= |
127e |
− j120 |
= 20 |
e |
− j |
210 = 20 |
e |
j150 = (−17,32 + j10) A; |
||||||||||
jωL |
|
|
|
|||||||||||||||||||
|
|
|
|
6,35e |
j90 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
= |
EC |
|
|
|
= |
127e j120 |
= 20 |
e |
j210 = 20 − j150 |
= (−17,32 − j10) A; |
|||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
I C |
|
− j ωC |
|
6,35e |
− j90 |
|
|
|
|
e |
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
I 0 = I A + I B + I C = 20 −17,32 + j10 −17,32 − j10 = |
||||||||||||||||||||||
= −14,64A =14,64e− j180 A.
В продолжение этого примера определим, чему должно равняться значение R, чтобы ток нулевого провода стал равен нулю.
Из векторной диаграммы (см. рис. 76) видно, что I 0 будет равен нулю, если модуль тока I А будет равен сумме модулей токов I B и I С , т.е. если I A = 34,64 A. Тогда
R = 127 = 3,67 Ом. 34,64
Соединение звезда-треугольник (см. рис. 71)
Ток I AB вызывается напряжением U AB . Модуль и фаза его относительно напряжения U AB определяются сопротивлением нагрузки Z АB . Ток I BC вызван напряжением U BC . Модуль и фаза его относительно U BC определяются сопротивлением Z BC . Ток I CA вызван напряжением U CA и зависит от сопротивленияZ CА.
Линейные токи вычисляются по соотношениям (52).
При равномерной нагрузке фаз линейные токи по модулю в
3 раз больше фазных токов нагрузки. При неравномерной нагрузке линейные токи могут быть и больше, и меньше фазных токов нагрузки.

102
Пример 22
Для схемы на рис. 71 задано: Z AB = − j19 Ом (емкостная на-
грузка); Z BC = j19 Ом (индуктивная нагрузка); Z CA =19 Ом. Э.д.с. каждой фазы генератора 220 В.
Требуется определить все токи схемы и построить векторную диаграмму.
Примем направление оси +1 вертикально вверх и в соответствии с векторной диаграммой фазных и линейных напряжений (см. рис. 74) определим линейные напряжения:
U AB |
= 220 |
|
|
3 |
e |
j30 = 380 j30 |
B; |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
||||
U B C |
= 380e − j 90 |
В; U C A = 380e j150 В. |
|
|
||||||||||||||||||||||
Токи в фазах нагрузки |
|
|
|
|
|
|
||||||||||||||||||||
I AB |
= |
|
|
U AB |
= |
|
380e j30 |
= 20 j120 |
= (−10 + j17,32) A; |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
Z AB |
|
|
|
19e− j90 |
|
e |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
380 |
− j90 |
|
|
|
|
|
|
|
|
|||||
I BC |
|
= |
|
U BC |
= |
|
|
|
|
e |
|
|
|
= 20e− j180 = −20 A; |
|
|
|
|||||||||
|
|
|
|
|
19e j90 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
Z BC |
|
|
|
|
|
|
|
|
|
|
|
||||||||
I CA |
= |
U CA |
|
= |
380e j150 |
= 20 j150 |
= (−17,32 + j10) A. |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
Z CA |
|
|
|
|
|
19 |
|
|
|
e |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Линейные токи определяем по (52): |
|
|
|
|||||||||||||||||||||||
I A = I AB − I CA = −10 + j17,32 +17,32 − j10 = 7,32 + j7,32 = |
|
|||||||||||||||||||||||||
= |
|
7,322 +7,322 |
e |
j arctg1 =10,35 |
j45 A; |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
||
I B = I BC − I AB = −20 +10 − j17,32 = −(10 + j17,32) = |
|
|
||||||||||||||||||||||||
= − 102 +17,322 |
e |
j arctg17,32 10 = −20 |
e |
j60 = 20 |
− j120 A; |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
||
I C |
= |
I CA |
− |
|
I BC |
= −17,32 + j10 + 20 = 2,68 + j10 =10,35 |
j75 |
A. |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
||||||||
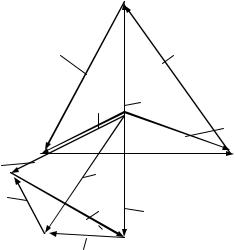
В соответствии с рассчитанными значениями токов и напряжений векторная диаграмма построена на рис. 77.
103
А
U CA |
|
U AB |
|
U C U А |
|
|
0 |
U B |
I AB C |
I CA |
U BC B |
I А |
I B |
I BC |
|
I C |
|
|
Рис. 77 |
|
Порядок построения следующий. Вначале строятся векторы фазных и линейных напряжений, затем — векторы токов фаз на-
грузки ( I AB опережает U AB на 90°, |
I BC отстает от U BC на 90°, |
I CA совпадает с направленем U CA ) |
и, наконец, по правилам вы- |
читания векторов в соответствии с (52) — векторы линейных токов.
Соединение звезда-звезда без нулевого провода (см. рис. 70)
Схема такого соединения представляет собой схему с двумя узлами. Поэтому для расчета токов здесь целесообразно пользоваться методом двух узлов (см. подраздел 2.6). Напряжение между узлами 0′ и 0
|
= E AY A |
+ |
E BY B |
+ |
ECY C |
( |
+ |
e |
− j120 |
Y B |
+ |
e |
j120 |
Y C |
) |
|
||
U 0′0 |
|
|
= |
E A |
Y A |
|
|
|
|
|
. (53) |
|||||||
|
|
|
|
|
|
Y A +Y B +Y C |
|
|
|
|||||||||
|
Y A +Y B +Y C |
|
|
|
|
|
|
|
||||||||||
Три вектора: 1; |
e− j120 и |
e j120 |
— образуют симметричную |
|||||||||||||||
трехфазную систему, подобную представленной на рис. 67, б. Следовательно, сумма рассматриваемых векторов равна нулю:
1+ e− j120 + e j120 = 0. |
(54) |
Если нагрузка равномерна (Y A = Y B =Y C ), то для рассматриваемого соединения с учетом (54) получим:
104
U 0′0 = E AY A(1+e− j120 +e j120 ) = 0.
3Y A
При этом напряжение на каждой фазе нагрузки равно соответствующей э.д.с.:
U A0′ = E A; U B0′ = E B; U C0′ = EC.
Если нагрузка неравномерна, то U 0′0 ≠ 0 и U A0′ = E A −U 0′0;
U B0′ = E B −U 0′0; U C0′ = EC −U 0′0.
Токи в фазах нагрузки:
I A =U A0′ Z A; I B =U B0′
Z A; I B =U B0′ Z B ; I C =U C0′
Z B ; I C =U C0′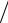 Z C .
Z C .
При наличии магнитно-связанных катушек расчет трехфазных цепей ведется так же, как и расчет магнитно-связанных цепей однофазного тока, т.е. на основе уравнений, составляемых по законам Кирхгофа.
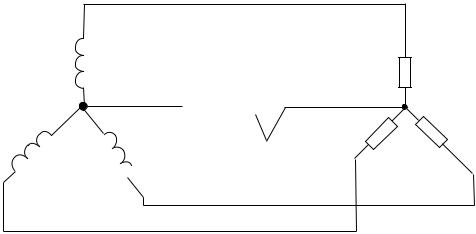
Пример 23
Для схемы на рис. 78 задано: Eф = 127 В; ωL =1 ωC = 4 Ом;
ωC = 4 Ом;
ωМ = 2 Ом. Требуется определить показания амперметра и вольтметра.
А |
|
А |
|
|
|
I А |
|
|
|
L |
M |
|
0 |
V |
0′ |
|
|
|
|
|
|
C |
L |
|
|
I B |
|
C |
|
В |
|
|
|
I C |
|
|
|
Рис. 78 |
|
Уравнение по первому закону Кирхгофа: |
|
||
|
|
I A + I B + I C = 0. |
(а) |
105
Уравнение по второму закону Кирхгофа для контура
0А0′В0:
I A jωL + I B jωM − I B jωL − I A jωM =U AB;
I A |
j4 + |
I B |
j2 − |
I B |
j4 |
− |
I A |
j2 |
= 220 |
j30 ; |
|
|
|
|
|
e |
|
||||
|
|
|
2 j(I A − I B) = 220e j30 . |
(б) |
||||||
Уравнение по второму закону Кирхгофа для контура
0С0′В0:
I С(− j ωC) − I B jωL − I A jωM =U CB;
ωC) − I B jωL − I A jωM =U CB;
−4 jI C −2 jI A −4 jI B = 220e j90 . |
(в) |
Из уравнения (б) выразим I A = I B −110e j120 |
и подставим в |
(а): |
|
I C = 110e j120 − 2 I B. |
|
Уравнение (в) преобразуем к виду
2I C + I А +2I B = −110
иподставим полученные значения I А и I C :
|
220e j120 − I B −110e j120 = −110 ; |
|
I B |
= 110(e j120 +1) = 110(−0, 5 + j0, 866 +1) = 110e j 60 A. |
|
|
I A = I B −110e j120 = 110(e j 60 − e j120 ) = |
|
|
= 110(0, 5 + j 0, 866 + 0, 5 − j 0, 866) = 110 A. |
|
ϕ0′ |
= ϕ0 + E A − I A jωL − I B jωM = 0 |
+127 − j110 4 − j220e j60 = |
=127 − j440 − j110 +190,5 = 317,5 |
− j550 = 635 − j60 B. |
|
|
|
e |
Таким образом, приборы покажут 110 А и 635 В.
Пример 24
Бытовые электрические сети выполняются однофазными, то есть в каждую квартиру жилого дома подается лишь одна из фаз трехфазной электрической системы. Подводится же к многоквартирному жилому дому трехфазная четырехпроводная сеть (три
106
линейных провода и нулевой, обмотки генератора соединены в звезду). В технической части подвального помещения есть распределительное устройство, от которого с помощью двухпроводных линий (от нулевого провода и одного из линейных проводов) электроэнергия распределяется по квартирам. К каждой фазе подключается примерно одинаковое количество квартир.
Электрические соединения на распределительном устройстве осуществляются с помощью болтов. Предположим, подсоединяющий нулевой провод трехфазного четырехпроводного кабеля болт при монтаже был плохо затянут. В месте контакта появилось сравнительно большое сопротивление, которое со временем увеличилось из-за окисления поверхности металла. В результате контакт все больше нагревался и в конце концов отгорел. То есть вместо схемы звезда-звезда с нулевым проводом образовалась схема звезда-звезда без нулевого провода.
Требуется определить, как исказятся напряжения в розетках квартир жилого дома при отгорании (или обрыве) нулевого провода на входе распределительного устройства, если фазное напряжение питающей сети 220 В, а эквивалентные сопротивления фаз нагрузки жилого дома в целом составляют 5 Ом, 10 Ом и 15 Ом (в предположении, что эти сопротивления чисто активные).
Решение поясняется схемой на рис. 79.
А
|
Z A |
0 |
0′ |
Z C |
Z B |
С В
В
Рис. 79
Будем считать Z A = 5 Ом, Z B = 10 Ом, Z C = 15 Ом.

107
По методу двух узлов
U 0′0 = |
E A |
Z A + E B Z B + EC Z C |
= |
|
|
|
|
|
|||
|
1 Z A +1 Z B +1 Z C |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
||
= |
220 5 + |
220 e− j120 10 + 220 e j120 |
15 |
|
= |
||||||
|
|
|
1 5 +1 10 +1 15 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
44 + 22 e− j120 +14,67 e j120 |
|
|
|
|||||
|
= |
|
|
|
|
|
= |
|
|
|
|
|
|
0,4 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||
|
= |
44 −11− j19,5 −7,34 + j12,7 |
= |
|
|
|
|||||
|
|
|
|
|
|
||||||
|
|
|
|
0,4 |
|
|
|
|
|
|
|
|
= |
25,65 − j6,35 |
= (64,13 − j15,88) |
B. |
|
||||||
|
|
|
|||||||||
|
|
|
0, 4 |
|
|
|
|
|
|
|
|
Напряжения на фазах нагрузки:
U A0′ = E A −U 0′0 = 220 −64,13+ j15,88 =155,87 + j15,88 =156,7 e j5,8 B; U B0′ = E B −U 0′0 = 220e− j120 −64,13 + j15,88 =
=−110 − j190,53 −64,13 + j15,88 =
=−174,13 − j174,65 = 246,6 e− j134,9 B;
U C0′ = EC −U 0′0 = 220e j120 −64,13 + j15,88 = = −110 + j190,53 −64,13 + j15,88 =
= −174,13 + j206,41 = 270 e j130,2 B.
Таким образом, напряжение сети в квартирах, подключенных к фазе А, будет составлять 156,7 В, к фазе В — 246,6 В, к фа-
зе С — 270 В.
4.3Активная, реактивная и полная мощности трехфазной системы
Под активной мощностью трехфазной системы понимают сумму активных мощностей фаз нагрузки и активной мощности сопротивления, включенного в нулевой провод:
108
P = P A + PB + PC + P0.
Реактивная мощность трехфазной системы представляет собой сумму реактивных мощностей фаз нагрузки и реактивной мощности сопротивления, включенного в нулевой провод:
Q = Q A +QB +QC +Q0.
Полная мощность S = P2 +Q2. Если нагрузка равномерная, то
P0 = Q0 = 0; P A = PB = PC =U фI фcosϕф;
Q A = QB = QC =U фI Фsin ϕф;
P = 3U фI фcosϕф; Q = 3U фI фsin ϕф;
S = 3U фI ф,
где ϕф — угол между напряжением U ф на фазе нагрузки и током I ф фазы нагрузки.
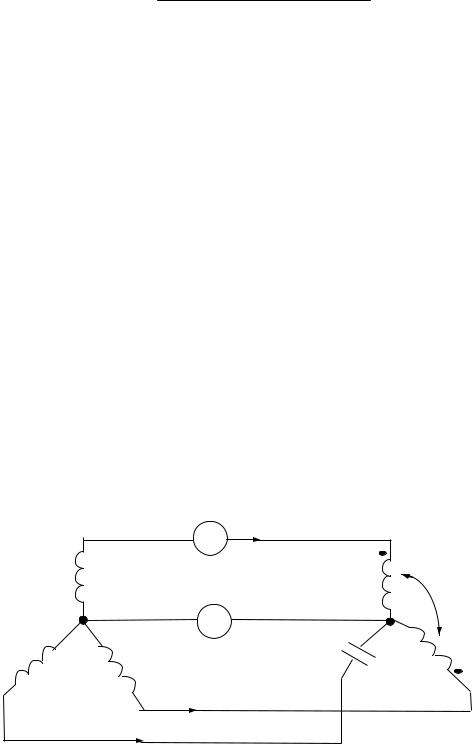
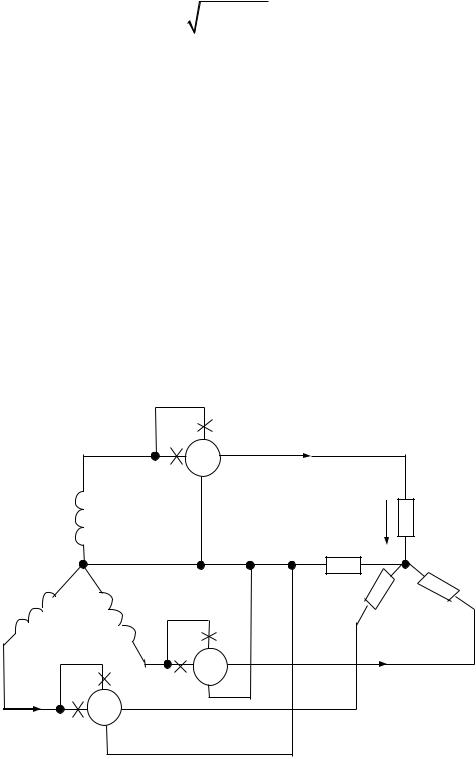
Для измерения активной мощности трехфазной системы в общем случае (неравномерная нагрузка и наличие нулевого провода) необходимо включать три ваттметра, как показано на рис. 80. Активная мощность системы равна сумме показаний трех ваттметров.
А |
W1 |
|
|
I A |
|
|
U A |
Z A |
0 |
Z 0′0 |
0′ |
Z B
Z C
|
I B |
|
B |
C |
W2 |
W3
I C
Рис. 80
109
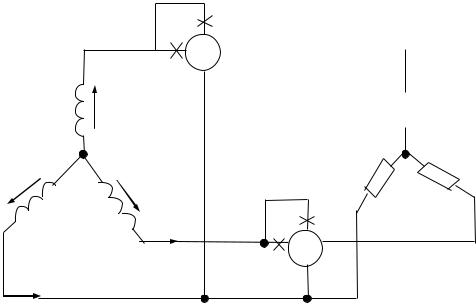
Если нулевой провод отсутствует, то измерение мощности производят двумя ваттметрами по схеме на рис. 81. Сумма показаний двух ваттметров при этом определяет активную мощность всей системы независимо от того, звездой или треугольником соединена нагрузка.
А  W1
W1
|
|
|
|
|
|
|
|
|
|
|
I A |
|
|
|
|
|
|
|
|
|
|
|
|
E A |
|
|
|
|
|
|
|
|
|
|
|
|
Z A |
|
|
|
|||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z C |
|
|
|
Z B |
|
|
|||
EC |
|
|
E B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
С |
|
|
В |
|
|
|
|
|
|
|
|
W2 |
|
|
|
|
|
|
|
|
|
|
I C |
|
|
|
I B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 81 |
|
|
|
|
|
|
|
|
|
|
|
|
||
Показание первого |
ваттметра |
равно |
|
|
|
, |
второго |
||||||||||||||
Re U AC IA |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− Re U BC IB . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Но |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Re |
|
|
|
|
|
|
= Re |
|
( |
|
− |
|
|
− |
|
|
|
|
= |
||
U AC |
I A + |
U BC |
I B |
|
|
|
U C |
) I A + ( |
U C |
) I B |
|
||||||||||
|
|
|
|
|
U A |
|
U B |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= Re U A I A + U B I B + U C I C , |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
так как I A + I B |
= − I C . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
