
ТОЭ / ТОЭ ТУСУР
.pdf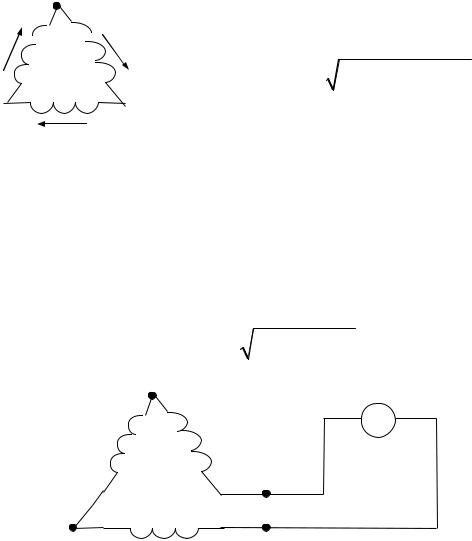
130
1. Если обмотки генератора соединены в треугольник, как показано на рис. 95, то по ним будут протекать токи гармоник, кратных трем, даже при отсутствии внешней нагрузки.
Алгебраическая сумма третьих гармоник э.д.с. в треугольнике равна 3Е3 . Обозначим сопротивление обмотки каждой фазы для третьей гармоники через Z 3 , тогда ток третьей гармоники в треугольнике равен:
I 3 |
= |
3E3 |
= |
E3 |
. |
|
3Z 3 |
Z 3 |
|||||
|
|
|
|
Аналогично для шестой, девятой и т.д. гармоник. Действующее значение тока, проте-
Акающего по замкнутому треугольнику в
схеме на рис. 95, равно:
Е3 
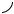 Е3
Е3
I |
I = |
2 |
+ |
2 |
+ |
2 |
+... . |
3 |
|
I 3 |
|
I 6 |
|
I 9 |
|
С
 В
В
Е3 Рис. 95
2. При соединении обмоток генератора в открытый треугольник по схеме на рис. 96 при наличии гармоник, кратных трем, на зажимах m и n будет напряжение
U mn = 3E3m sin(3ωt +ϕ3) +3E6m sin(6ωt +ϕ6) +....
Показание вольтметра будет равно:
U = 3 E32 + E62 +... .
V
m
n
Рис. 96
131
3. В линейном напряжении вне зависимости от того, звездой или треугольником соединены обмотки генератора, кратные трем гармоники отсутствуют.
Докажем это свойство для случая холостого хода генератора, т.е. когда внешняя нагрузка отсутствует. Но оно остается в силе и при наличии нагрузки.
Рассмотрим сначала схему соединения треугольником (см. рис. 95). Обозначим ϕА3 — потенциал точки А и ϕB3 — потенци-
ал точки В по третьей гармонике, получим
ϕА3 = ϕB3 − E3 + I 3Z 3.
Но E3 = I 3Z 3, следовательно, ϕА3 = ϕB3.
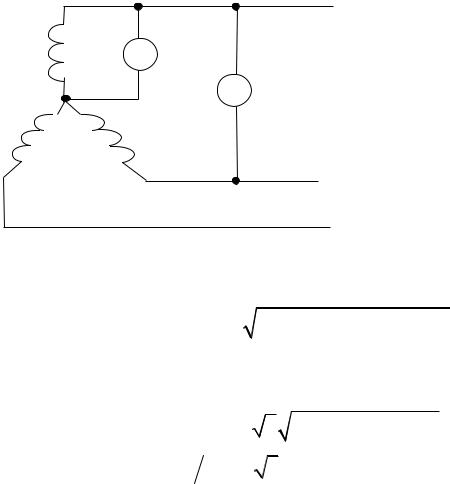
При соединении в звезду
Vф
Vл
Рис. 97
(рис. 97) линейное напряжение третьей гармоники равно разности соответствующих фазных напряжений. Так как третьи гармоники в фазных напряжениях совпадают по фазе, то при составлении этой разности они вычитаются.
В фазном напряжении могут присутствовать все гармоники. Поэтому действующее значение фазного напряжения
U ф = U12 +U 22 +U 32 +U 24 +... .
В линейном напряжении (см. рис. 95) отсутствуют гармоники, кратные трем, поэтому
U л = |
3 |
U12 +U 22 +U 42 +... . |
Отношение U л U ф < |
3 , |
если есть гармоники, кратные |
трем.

132
4. При соединении генератора и равномерной нагрузки в звезду и отсутствии нулевого провода токи кратных трем гармоник по линейным проводам не протекают. Поэтому между нулевыми точками приемника 0′ и генератора 0 будет действовать напряжение
u0′0 = E3m sin(3ωt + ϕ3) + E6m sin(6ωt + ϕ6) +....
Действующее значение его
U 0′0 |
= E32m + |
E62m |
+.... |
|
2 |
||||
|
2 |
|
5. Если в схеме звезда-звезда с нулевым проводом при равномерной нагрузке фаз сопротивление нагрузки для третьей гармоники обозначить Z н3 , а сопротивление нулевого провода для третьей гармоники обозначим Z03 , то по нулевому проводу будет протекать ток третьей гармоники, равный:
I 03 = |
|
E3 |
. |
|
Z 03 |
+ Z н3 |
|||
|
|
|||
|
|
3 |
|
|
По каждому из линейных |
проводов будет протекать ток |
|||
третьей гармоники I 03 3.
3.
Аналогично находятся токи и от других гармоник, кратных трем.
133
6 ТЕОРИЯ ЧЕТЫРЕХПОЛЮСНИКА. ФИЛЬТРЫ
6.1 Основы теории пассивного четырехполюсника
Генератор и приемник обычно соединяются через промежуточную цепь, в общем случае сколь угодно сложную. Каждая из таких цепей имеет два входных зажима (к ним подсоединяется генератор) и два выходных (к ним подсоединяется нагрузка). Отсюда и название — четырехполюсник.
Основными уравнениями четырехполюсника называются линейные зависимости, связывающие его входные и выходные величины. Исходя из этих уравнений, можно любой сложный четырехполюсник заменить одной из простых эквивалентных схем, что существенно упрощает расчет и исследования.
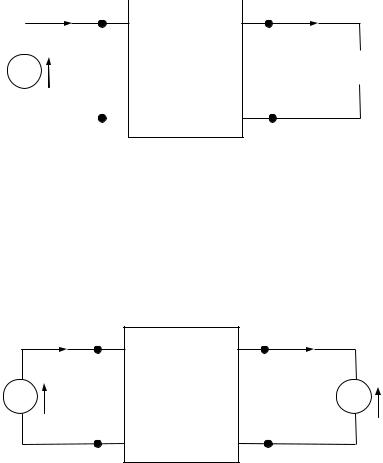
Схема на рис. 98 иллюстрирует соединение генератора с э.д.с. E1 и нагрузки Z 2 через пассивный четырехполюсник.
I1 m |
|
p I 2 |
|
|
|
|
|
|
|
|
|
|
|
~ E1 |
|
|
Z 2 |
|
|
n |
q |
|
|
|
||||
|
|
|
|
|
Рис. 98
Заменим нагрузку Z 2 на э.д.с. E2 , направленную встречно току I 2 и численно равную напряжению U 2 на нагрузке Z 2 , как
показано на рис. 99. Такая замена возможна согласно теореме компенсации (см. подраздел 2.9).
I1 m |
p I 2 |
~ E1 |
~ E2 |
n |
q |
Рис. 99
134
Запишем выражения для токов через э.д.с. и входные и взаимные проводимости ветвей (т.е. используем метод наложения):
I1 |
= E1Y11 |
− E2Y12; |
(61) |
|
|
|
(62) |
I 2 = E1Y12 − E2Y 22. |
|||
• • •
Примечание. Под входными проводимостями понимаются проводимости, имеющие в формулах (61), (62) одинаковые индексы, а под взаимными — проводимости, имеющие разные индексы.
Ветвь цепи с источником E1 (см. рис. 97) будем называть первой, а ветвь с источником E2 — второй.
Через входную проводимость (например Y11) можно определить ток в ветви (первой) с источником э.д.с. ( E1), если остальные э.д.с. в цепи равны нулю ( E2 =0).
Через взаимную проводимость (Y12 ) можно определить ток в ветви (например, второй) без источника э.д.с. (при E2 =0) от источника э.д.с. ( E1), расположенного в другой ветви (первой).
• • •
Из (62) получим: |
|
|
|
|
|
1 |
|
|
|
|
|
E1 |
= E2 Y 22 + I 2 |
. |
|
|
(63) |
||||
|
|
|
|
|||||||
Подставим (63) в (61): |
|
Y12 |
|
Y12 |
|
|
|
|||
Y11Y 22 −Y122 |
|
|
|
|
|
|||||
I1 |
= E2 |
+ I 2 |
Y11 |
. |
(64) |
|||||
|
Y12 |
|
Y12 |
|||||||
Введем обозначения: |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
|
|
A = Y 22 ; |
|
|
|
|
|
|
||
|
|
|
|
Y12 |
|
|
|
|
|
|
|
|
C = |
Y11Y |
12 −Y122 |
|
|
|
|||
|
|
|
|
; |
|
|
|
|||
Y12

135
B = |
1 |
|
|
|
; |
|
|
Y12 |
|
||
|
|
(65) |
|
|
|
|
D= Y11 . Y12
Коэффициенты А, В, С, D называются постоянными четырехполюсника. А и D — безразмерные, В имеет размерность со-
противления, С — проводимости. |
|
|
|
|
|
|
|
||
Заменив в (63) и (64) E1 на U1 и E2 |
на U 2 , получим основ- |
||||||||
ные уравнения четырехполюсника: |
|
|
|
|
|
|
|
||
U1 |
= A |
|
+ B |
|
; |
|
(66) |
||
U |
2 |
|
|
I 2 |
|
||||
I1 = CU 2 + DI 2. |
|
|
|||||||
Найдем определитель этой системы: |
|
|
|
||||||
AD − BC = |
Y11Y 22 |
− |
Y11Y |
22 |
−Y122 |
=1. |
|||
|
Y122 |
|
Y122 |
||||||
|
|
|
|
|
|
||||
Поменяем местами источник и приемник, как показано на рис. 100.
|
|
I 2 m |
|
|
|
|
|
|
|
p I1 |
|
||
|
|
|
|
|
|
|
|
||||||
|
|
Z 2 |
|
|
|
|
|
|
|
|
|
~ |
E1 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
n |
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Рис. 100 |
|
|
|
|
|
|
||
Если здесь также заменить |
Z 2 |
на э.д.с. E2 , направленную |
|||||||||||
встречно I 2 , то получим: |
= − |
|
+ |
|
|
|
; |
|
|||||
|
|
I 2 |
Y |
|
Y |
(67) |
|||||||
|
|
|
|
E2 11 |
|
E1 |
|
12 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
(68) |
|
|
|
I1 = −E2Y12 + E1Y 22. |
|||||||||||
Из (67) следует |
|
|
|
|
|
|
|
1 |
|
|
|||
|
|
E1 |
= E2 Y11 + I 2 |
|
. |
(69) |
|||||||
|
|
|
|
||||||||||
|
|
|
|
|
|
Y12 |
|
|
Y12 |
|
|||
136
Подставим (69) в (68):
I1 |
= E2 |
Y11Y 22 −Y122 |
+ I 2 |
Y 22 |
. |
(70) |
|
Y12 |
Y12 |
||||||
|
|
|
|
|
Заменив в (69) и (70) E1 на U1 , E2 на U 2 , получим:
U1 |
= D |
+ B |
; |
(71) |
U 2 |
|
I 2 |
||
I1 = CU 2 + АU 2. |
|
|||
Сравнивая системы уравнений (66) и (71) для прямого (см. рис. 80) и обратного (см. рис. 92) включений четырехполюсника, можно видеть, что поменялись местами постоянные А и D.
Четырехполюсник называют симметричным, если при перемене местами источника и нагрузки токи в источнике и нагрузке не изменяются. В симметричном четырехполюснике А=D.
Комплексные коэффициенты А, В, С, D можно определить по формулам (65), если схема внутренних соединений четырехполюсника и ее параметры известны, либо используя входные сопротивления четырехполюсника, полученные опытным или расчетным путем.
Определим комплексное входное сопротивление четырехполюсника при трех различных режимах его работы.
1. Комплекс входного сопротивления со стороны зажимов mn при разомкнутой ветви pq (холостой ход ветви pq):
Z1x = z1xe jϕx. |
(72) |
2. Комплекс входного сопротивления со стороны зажимов mn при коротком замыкании зажимов pq (короткое замыкание ветви pq):
Z1к = z1кe jϕ1к. |
(73) |
3. Комплекс входного сопротивления со стороны зажимов pq при коротком замыкании зажимов mn:
Z 2к = z2кe jϕ2к. |
(74) |

137
Из системы (66) при холостом ходе ветви pq, получим
U1x = AU 2x; I1x = CU 2x.
Отсюда комплекс входного сопротивления
Z1x = U1x = A . I1x C
При коротком замыкании ветвей pq, когда U 2 =
U1к = BI 2к; I1к = DI 2к,
следовательно,
Z1к = U1к = B .
I1к D
когда I 2 = 0,
0,
При обратном питании и коротком замыкании входных зажимов (см. рис. 100) U 2 = 0, поэтому из (71) следует:
U1к = BI 2к; I1к = АI 2к;
Z 2к = U1к = B . I1к А
Таким образом, для определения четырех неизвестных имеем четыре уравнения:
|
AD − BC =1; |
|
(75) |
||||||
|
Z1x = A C ; |
|
|
(76) |
|||||
|
|
|
|||||||
|
Z1к = B D; |
|
|
(77) |
|||||
|
|
|
(78) |
||||||
|
Z 2к = B A. |
|
|
|
|
|
|||
|
|
|
|
|
|
||||
Составим разность |
|
|
|
|
|
|
|
|
|
1− Z1к =1− |
BC |
= |
AD − BC |
= |
1 |
, |
|||
|
|
|
|||||||
Z1x |
|
DA |
|
DA |
|
DA |
|||
или |
Z1x − Z1к |
|
1 |
|
|
|
|
||
|
= |
. |
(79) |
||||||
|
Z1x |
AD |
|||||||
|
|
|
|
|
|
||||
|
|
138 |
|
|
|
|
|
|
|
|
|
Поделим (78) на (77): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z 2к |
= |
D |
. |
|
|
|
(80) |
|
|
|
|
Z1к |
A |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||
Умножим (79) на (80): |
|
|
|
|
|
|
|
|
|
|
|
|
(Z1x − Z1к) Z2к |
= |
1 |
|
; |
|
|||||
|
|
Z1x Z1к |
|
|
A 2 |
|
|
||||
A = |
|
Z1xZ1к |
|
. |
(81) |
||||||
|
(Z1x |
− Z1к)Z 2к |
|||||||||
|
|
|
|
|
|
||||||
Таким образом, вначале по (81) рассчитывается постоянная четырехполюсника А, затем по (76) определяется постоянная С, по (78) — постоянная В и по (77) — постоянная D.
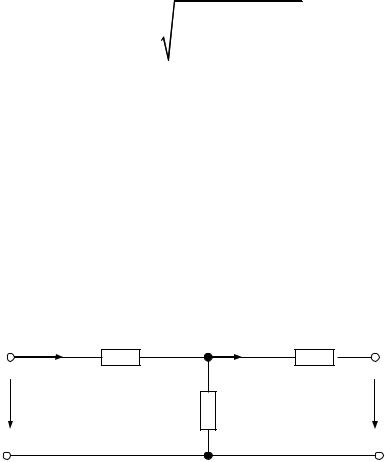
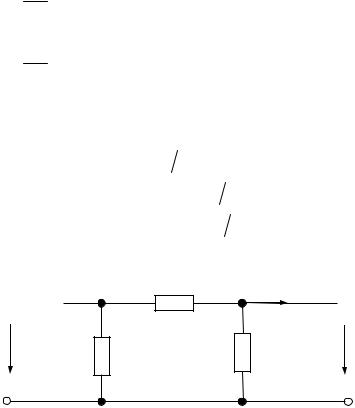
Функции сколь угодно сложного пассивного четырехполюсника как передаточного звена между источником и нагрузкой могут выполнять (при фиксированной частоте) простейшие электрические схемы, называемые схемами замещения четырехполюсника: Т-схема замещения (см. рис. 101) и П-схема замещения
(см. рис. 102).
I1 |
Z1 |
I 2 |
Z 2 |
m |
|
|
p |
U1 |
|
Z 3 |
U 2 |
n |
|
Рис. 101 |
q |
|
|
|
Три сопротивления Т- или П-схем замещения должны быть рассчитаны исходя из того, чтобы схема замещения обладала такими же коэффициентами А, В, С, D, какими обладает заменяемый ею четырехполюсник. Задача эта однозначна, так как схема замещения содержит три элемента и четырехполюсник характеризуется тоже тремя параметрами (одна связь между А, В, С, D задана уравнением AD − BC =1).
139
Выразим напряжение U1 и ток I1 в Т-схеме (см. рис. 101)
через напряжение U 2 и ток I 2 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
U 2 + I |
2Z 2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
Z 2 |
|
|
|||
I1 = I 2 + |
|
|
|
|
=U 2 |
|
+ I 2 |
1+ |
|
; |
(82) |
|||||||||
|
Z 3 |
|
Z 3 |
Z 3 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
Z1 |
|
|
|
|
|
|
Z 2 |
|
|
|
||||
U1 =U 2 + I 2Z 2 + I1Z1 =U 2 |
+U 2 |
|
|
+ I 2 1 |
+ |
|
|
|
Z1 |
+ I 2Z 2 = |
||||||||||
Z 3 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Z 3 |
|
|
|
|||||
|
|
Z1 |
|
|
|
|
|
Z 2Z1 |
|
|
|
|
|
|
|
|||||
=U 2 1+ |
|
+ I 2 Z1 |
+ |
|
|
|
|
+ Z 2 |
. |
|
|
(83) |
||||||||
|
|
Z 3 |
|
|
||||||||||||||||
|
|
Z 2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Сопоставим (82) и (83) с (66) и найдем
A =1+ Z1 ;
Z 3
C = 1 ;
Z 3
Следовательно,
I1
m 
B = Z1 + Z |
2 + |
Z1Z |
2 |
|
|
|
|
; |
|||
|
|
||||
|
|
|
Z 3 |
|
|
D =1+ |
Z 2 |
. |
|
|
|
Z 3 |
|
|
|
||
|
|
|
|
|
|
Z 3 =1 С; |
|
Z1 = (A −1) |
|
C; |
|
Z 2 = (D −1) |
|
C. |
|
Z 4 |
I 2 |
 p
p
(84)
(85)
U1 |
Z 5 |
Z 6 |
U 2 |
n |
|
Рис. 102 |
q |
|
|
|
Аналогичные выкладки для П-схемы (см. рис. 102) дают:
A =1+ Z 4 ; B = |
; C = Z 4 + Z 5 + Z 6 |
; D =1+ Z 4 . |
Z 6 |
Z 4 |
Z 5 |
Z 5Z 6 |
