Nugmanov

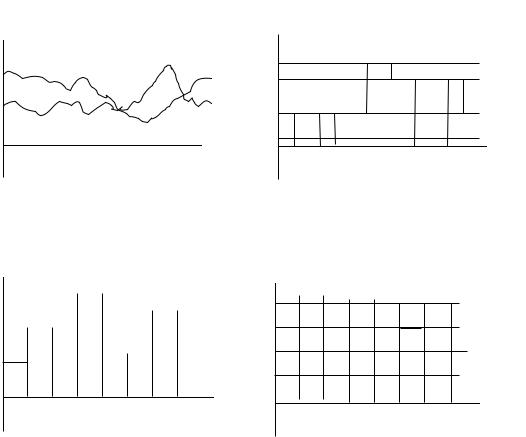
1.Случайные процессы

1.1.Функция распределения случайного процесса

Детерминированный процесс полностью определяется значением аргумента t . Для случайного процесса нельзя задать однозначное соответствие между аргументом и значениями функции. Одному значению аргумента может соответствовать множество значений функции, одни из которых более вероятны, другие - менее вероятны.

Случайный процесс ξ(t) - это функция времени, которая при любом значении времени t есть случайная величина. Во время эксперимента наблюдаются конкретные значения x(t) случайного процесса ξ(t) , которые называются реализациями случайного процесса. Случайный процесс ξ(t) классифицируют по пространственно-временным признакам и по вероятностным характеристикам.

В общем случае и время t , и пространство значений x(t) случайного процесса ξ(t) принимают непрерывные значения. Такой процесс называется процессом общего типа, Рис. 1.1.

3

Если рассматриваются непрерывные значения времени t , а значения x(t) случайного процесса ξ(t) дискретны, то такой процесс называется дискретным процессом, Рис. 1.2. Если время t принимает дискретные значения, а значения x(t) случайного процесса ξ(t) непрерывны, то такой процесс называется последовательностью общего типа, Рис. 1.3.

Если время t принимает дискретные значения и значения x(t) случайного процесса ξ(t) тоже дискретны, то такой процесс называется дискретной случайной последовательностью, Рис. 1.4.

Для всех типов случайных процессов необходимо задать (определить) область ξ возможных значений x(t) случайного

процесса ξ(t) . В частности, случайный процесс ξ(t) может принимать значения в интервале ( , ) , т.е. ξ : x(t) .

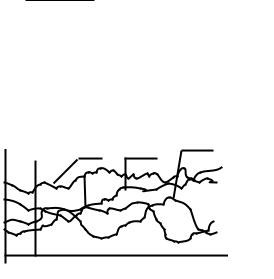
Рассмотрим r реализаций x(1) (t1), x(2) (t1), , x(r) (t1) случайного процесса ξ(t) в момент времени t1 (Рис 1.5) и зададим некоторый порог x1. Из множества r реализаций выберем те m(x1, t1 )

величины x1. Эта вероятность зависит от величины x1, времени t1 и

называется одномерной функцией распределения случайного процесса ξ(t)

4

Точно по такой же методике можно составить многомерную функцию распределения

Wξ (x1, x 2 , , x k , t1, t 2 , , t k )

отражающую вероятность того, что значения случайного процесса в моменты времени t1, t 2 , , t k не превысят соответствующих значений x1, x 2 , , x k .

Таким образом, случайный процесс ξ(t) можно описать многомерной функцией распределения (1.2). Чем больше точек отсчета k функции распределения, тем более полно описан случайный процесс. Необходимое количество точек отсчета k в исследуемой функции распределения зависит от решаемой проблемы.

Для процесса общего типа и для последовательности общего типа вводится одномерная плотность распределения вероятности:

или многомерная плотность распределения вероятности,

w(x1, xk , t1, tk ) dk W(x1, xk , t1, tk ) . (1.4) dx1 dxk

Используя формулы (1.3) и (1.4) , запишем интегральные формы одномерной и многомерной функций распределения

Для дискретного процесса и дискретной случайной последовательности вводится совместная вероятность того, что

5

Одномерная и многомерная функции распределения дискретного процесса и дискретной случайной последовательности будут иметь

x1 x m x k x j

где xm ,..., x j - значения случайного процесса на дискретном множестве x .

Функция распределения вероятности обладает свойствами:

1. функция распределения является неубывающей функцией, т.е.

если x1 x2 , то W(x1, t1) W(x 2 , t 2 ) ,

W(x1, t1) W(x2 , t 2 / x1, t1) W(x2 , t 2 ) W(x1, t1 / x 2 , t 2 ), W(x1, x k , t1, , t k )

W(x1, t1) W(x 2 , t 2 / x1, t1) W(x k , t k / x k 1, t k 1, , x1, t1).

4. W( , x 2 , t1, t 2 ) W(x 2 , t 2 ),

W(x1, x j 1, , x j 1, , x k , t1, , t j , , t k )

W(x1, x j 1, x j 1, , x k , t1, , t k ).

Если ξ(t) - дискретный случайный процесс, то процесс описывается вероятностью P ξ(ti ) xk p(xk , ti ) - реализации x k случайного процесса в момент t ti , и функция распределения вероятности дискретного случайного процесса определена как

P ξ(ti ) x p(x j , ti ) .

x j x

Плотность распределения вероятности обладает следующим свойствами:

1.плотность распределения– неотрицательная функция w(x1, t1) 0, . . . , w(x1, x k , t1, t k ) 0,

6

2. должно соблюдаться условие нормировки

w(x1, t1) dx1 1,

w(x1, , x k , t1, , t k )dx1 dx k 1.

w(x1, , x j 1, x j 1, , x k , t1, , t j 1, t j 1, , t k )

5.Размерность одномерной плотности распределения вероятности

измеряемой величины (ток, напряжение, давление и т.д.).

7

1.2. Моментные функции случайного процесса

Плотность распределения вероятности w(x1, x k , t1, , t k ) и функция распределения вероятности W(x1, x k , t1, , t k ) полностью описывают случайный процесс ξ(t) . Функции распределения вероятности учитывают особенности случайного процесса. И чем больше точек отсчета t i , тем полнее описан процесс. Однако на практике часто встречаются задачи, в которых достаточно знать некоторые функции, характеризующие случайный процесс, такие как изменение среднего значения процесса во времени, энергию процесса, степень влияния одних значений процесса на другие и т. д. Эти функции называются моментными функциями случайного процесса.

Различают начальные, центральные и смешанные моментные функции.

Начальной моментной функцией k -го порядка называется неслучайная функция времени, которая имеет следующий вид

В частности, если k =1, начальная моментная функция первого порядка называется математическим ожиданием случайного процесса,

математического ожидания x – размерность измеряемой величины x.

Центрированной моментной функцией k -го порядка относительно величины mξ (t) называется неслучайная функция вида

Дисперсия Dξ(t) характеризует степень разброса значений случайного процесса около математического ожидания. Размерность дисперсии - x 2 – квадрат измеряемой величины x. Если ξ(t) - ток или напряжение, то дисперсия Dξ(t) пропорциональна мгновенной мощности, выделяемой на сопротивлении в 1 Ом.

Смешанной моментной функцией (j, k)-го порядка называется неслучайная функция вида

p(xi , x m , t1, t 2 ) - совместная вероятность реализации значений xi и x m случайного процесса ξ(t) в моменты времени t1, t 2

В частности для j k 1имеем смешанную моментную функцию первого порядка, называемую корреляционной функцией -

Bξ (t1, t 2 ) M(ξ(t1) ξ(t 2 )).

Если значения случайного процесса центрированы относительно математического ожидания, для j k 1 имеем ковариационную функцию

9

Корреляционная и ковариационная функции характеризуют степень статистической связи между значениями случайного процесса в моменты времени t1 и t 2 и имеют размерность, равную

размерности квадрата измеряемой величины – [ x 2 ].

10

1.3. Стационарный случайный процесс

Ранее была произведена классификация случайных процессов по

времени и пространству значений случайного процесса. С точки

зрения вероятностных характеристик случайные процессы делятся на

стационарные и нестационарные. Стационарные процессы в свою

очередь подразделяются на процессы стационарные в узком смысле

(строго стационарные) и широком смысле.

Случайный процесс (t) называется стационарным в узком смысле, если функция распределения и плотность распределения инвариантны относительно сдвига во времени, т.е. они не меняются при любом сдвиге всей группы точек t1, t 2 , , t m вдоль оси времени на одну и ту же величину t 0 :

W(x1, , x m , t1, , t m ) W(x1, , x m , t1 t 0 , , t m t 0 ), w(x1, , x m , t1, , t m ) w(x1, , x m , t1 t 0 , , t m t 0 ).

Случайный процесс, не обладающий этим свойством, называется x(t) w(x) нестационарным в узком смысле. Стационарный случайный процесс - это установившийся процесс и реализуется при неизменных

внешних условиях.

W(x1, t1) W(x1, t1 t 0 ) W(x1 ),

w(x1, t1) w(x1, t1 t 0 ) w(x1)

11

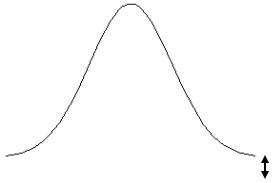
- двумерная функция распределения вероятности и плотность распределения вероятности зависят от разности моментов времени t1, t 2

- многомерная плотность распределения вероятности запишется как

Как видно из приведенных формул, математическое ожидание и дисперсия не зависят от времени, а корреляционная и

ковариационная функции зависят от разности моментов времени.

Стационарность в широком смысле. Случайный процесс называется стационарным в широком смысле, если математическое

12