Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Казанский федеральный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Nugmanov

.pdf

Скачиваний:

Добавлен:

10.02.2015

Размер:

1.6 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 94 5 6 7 8 9 > Следующая >>>

ξ(k) (t)

Tн / 2

Tн τ / 2

Tн

Tн / 2

Tн τ / 2

B0ξ (τ)

dt 0

dt 0 dτ

B0ξ

(τ)

dt 0

dτ

Tн Tн

τ / 2

Tн / 2

Tн

τ / 2

Tн / 2

Tн

B0ξ (τ) Tн τ dτ

Tн

(τ) 1

dτ

(τ) dτ .

(1.47)

0ξ

Tн T

Tн

Tн T

Таким

образом,

для

выполнения

критерия

lim D ξ k (t) 0

Tн

достаточно выполнения условия

Tн

lim

B0ξ (τ) dτ 0,

(1.48)

Tн Tн T

которое называется условием эргодичности Слуцкого.

Если условие Слуцкого выполняется, то процесс ξ(t) можно считать эргодическим по отношению к среднему по времени и

использовать среднее по времени 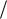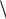для оценки

математического ожидания M(ξ(t)) . Время наблюдения необходимо взять достаточно большим, но не настолько большим, чтобы нарушились условия, обеспечивающие стационарность исследуемого процесса.

Если рассматривается другая числовая характеристика,

вычисленная по времени,	скажем, корреляционная	функция
η(τ) ξ(k) (t) ξ(k) (t τ) , то	для применения условия	Слуцкого

необходимо вычислить соответствующую ковариационную функцию

и проверить выполнение условия (1.39). Для процесса η(τ) необходимо вычислить B0η (ν) . При выполнении условия

Tн

lim 1 B (ν) dν 0

Tн Tн Tн 0η

можно говорить, что процесс ξ(t) - эргодический по отношению

к ковариационной функции процесса η(τ) .

Пример 4.1. Пусть процесс ξ(t) - стационарный случайный

процесс с ковариационной функцией B0ξ (τ) m сos ω0τ . Доказать,

что процесс ξ(t) - эргодический процесс.

Ковариационная функция

B0ξ (τ) B0ξ (t 2 t1)

при

t 2 t1

не стремится к нулю. Поэтому используем условие Слуцкого

Tн

sin ω0Tн

B0ξ (τ) dτ

2 m

0 .

Tн

0 н

Tн

Условие Слуцкого выполняется. Следовательно, процесс ξ(t) -

эргодический по отношению к среднему по времени.

Пример 4.2. Найти условие эргодичности по отношению к среднему по времени для случайного процесса η(t) k ξ(t) Y b ,

где k – постоянная величина, не равная нулю, ξ(t) - стационарный эргодический случайный процесс с Mξ(t) mξ , Dξ(t) σξ2 , Y –

случайная величина с MY mY , DY σ2Y , процесс ξ(t) и величина

Y - независимы, b – постоянная величина.

1.Вычислим η(t) k (ξ(t) mξ ) (Y mY ) k ξ(t) Y,

о о

2.Вычислим B0η (t1, t 2 ) M(η(t1) η(t 2 ))

k 2 B

0ξ

, t

) σ2

k 2 B

0ξ

) σ2

0η

3. Из

полученной

формулы

для

ковариационной

функции

B0η (t1, t 2 ) видно, что ковариационная функция с увеличением

разности t 2 t1 стремится к постоянной величине σ 2Y , а не к нулю,

как того требует условие эргодичности. Более того, если произвести проверку эргодичности процесса η(t) по условию Слуцкого, то увидим, что оно нарушается.

Следовательно, для того, чтобы процесс η(t) был эргодическим необходимо отсутствие случайной величины Y. Тогда в выражении для B0η (t1, t 2 ) будет отсутствовать величина σ 2Y и процесс η(t)будет эргодическим. Постоянные величины k и b не влияют на условие эргодичности исследуемого процесса.

Пример 4.3. Рассмотрим, как оценивается одномерная плотность

распределения

вероятности w ξ (x) случайного

эргодического

процесса ξ(t)

по одной единственной k-ой реализации ξ(k) (t) , (Рис.

1.12).

Преобразуем

(k)(t)

процесс

ξ(t)

в новый

процесс η(t), который

vi+v

принимает

значения

y0 0 ,

если

процесс

(t)

ξ(t) не

принадлежит

интервалу

tig

tig+ ij

Рис.1.12

(vi , vi v), и y1 1, если процесс ξ(t) находится в интервале

(vi , vi v). В результате образуется последовательность единичных импульсов y(k) (t) , появляющихся в случайные моменты времени t ig

и со случайной длительностью τi j , (индекс i при моментах времени

t ig и τi j означает, что вычисляется распределение плотности

вероятности для v vi ):

1,	если v			ξ(k) (t) v		v
		i			i
y(k) (t)		i			i
0,	если v		i	ξ(k) (t) или ξ(k) (t) v			i	v.
			i				i

Вычислим среднее по времени процесса η(t):

		T			ti g τi j
η(k) (t)	1	н y(k) (t) dt	1		y(k) (t) dt	1	τi j .
η(k) (t)	T	н y(k) (t) dt	T		y(k) (t) dt	T	τi j .
	н	0	н	j	ti g	н	j

Среднее по ансамблю процесса η(t) равно

Mη(t) 1 P(η(t) 1) 0 P(η(t) 0) P(vi ξ(t) vi v)

	vi v
	w(v) dv w(vi ) v .
	vi

Докажем, что процесс η(t) эргодический. Рассмотрим

ковариационную функцию процесса η(t).

B0η (t1, t 2 ) M(η(t1), η(t 2 )) Mη(t1) Mη(t 2 ).

Корреляционная функция процесса η(t)имеет вид

1 1

Bη (t1, t 2 ) M(η(t1), η(t 2 )) yi y j P(η(t1) yi , η(t 2 ) y j )=

i 0j 0

			v v v v
P(η(t1) 1, η(t 2 ) 1)				w ξ (v1, v2 , t 2 t1) dv1 dv2 .
			v	v
Подставим значения Bη (t1, t 2 ) и Mη(t) в B0η (t1, t 2 )
	v v v v
B0η (t1, t 2 )		(w ξ (v1, v2 , t 2 t1) w ξ (v1, t1) w ξ (v2 , t 2 )) dv1 dv2

B0η (t 2 t1) .

Как видно из предыдущего выражения, поведение

ковариационной функции зависит от поведения совместной плотности распределения w ξ (v1, v2 , t 2 t1) при t 2 t1 . Если

статистическая связь между значениями v1 и v2 случайного процесса

ξ(t) исчезает при

t 2 t1

, то

w ξ (v1, v2

, t 2 t1)

w ξ (v1, t1) w ξ (v2 , t 2 ),

и B0η (t 2 t1) 0

при

t 2

что является достаточным

условием эргодичности процесса η(t).

Учитывая, что процесс η(t) - эргодический, при достаточно

большом времени наблюдения Tн можно записать

τi j

w(v j ) v

или

w(vi )

τi j .

(1.49)

v T

н j

Разделив возможные значения v случайного процесса ξ(t) на интервалы с шагом v, определим величину плотности распределения вероятности для каждого i-го интервала при помощи

(1.49).

1.7. Спектральная функция стационарного случайного процесса

При изучении спектральных свойств детерминированных процессов используется преобразование Фурье. Переход от временного представления процесса к частотному отображению позволяет исследовать амплитудные и фазовые характеристики процесса как функцию частоты. Обратное преобразование Фурье

позволяет восстановить исследуемый процесс.

Однако применить непосредственно преобразование Фурье к анализу случайных процессов невозможно, т.к. случайному процессу

ξ(t) соответствует множество возможных реализаций x(t) ξ(k) (t) и

для каждого из них можно применить преобразование Фурье. В

результате нельзя однозначно отождествить обратное преобразование Фурье со случайным процессом ξ(t) . Поэтому для описания процесса

ξ(t) пользуются усредненной спектральной характеристикой.

Рассмотрим стационарный случайный процесс ξ(t) . Для каждой

реализации	ξ(k) (t) на интервале времени ( T	/ 2, T / 2) найдем
	н	н

преобразование Фурье и рассчитаем квадрат модуля преобразования

Фурье	FξT	( jω) , приходящуюся	на единицу полосы		частот.
	н
Определим		математическое	ожидание	квадрата	модуля
преобразования Фурье FξT ( jω) . Предел этой величины при					Tн
		н

называют спектральной плотностью Fξ (ω) случайного процесса ξ(t)

Покажем связь спектральной плотности Fξ (ω) случайного

процесса (t) с корреляционной функцией B ( ) .
Пусть известна реализация ξ(k) (t) на интервале ( T									/ 2, T / 2).
								н	н
Преобразование Фурье этой реализации имеет вид
			T	/ 2
	FξT	( jω)	н			ξ(k) (t) exp( j ω t) dt .
	н		Tн / 2
			Tн / 2
Рассмотрим		квадрат				модуля преобразования Фурье			FξT ( jω)
									н
данной реализации, приходящуюся на единицу полосы частот 1/ Tн
	F	(ω)	1		F		( jω)	2 .
			1

	ξT				ξT
	н		Tн			н
			Tн
Усреднив FξT (ω) по всем возможным реализациям на интервале
		н
времени	( t ) ,				получим спектральную плотность Fξ (ω)
случайного процесса ξ(t) :

M F

(ω) lim

F (ω)

lim

ξTн

Tн

Вычислим

( jω)

ξTн

Tн

Tн / 2

(k)

jω(t2 t1)

Tн

(t1) ξ

(t 2 ) e

Tн / 2 Tн / 2

	T / 2	T / 2
1	н	н	Bξ (t 2 t1 ) e	jω (t2	t1) dt1 dt 2 .
	н	н	Bξ (t 2 t1 ) e	jω (t2	t1) dt1 dt 2 .
Tн T / 2		T / 2
	н	н

( jω) . (1.50)

dt1 dt 2

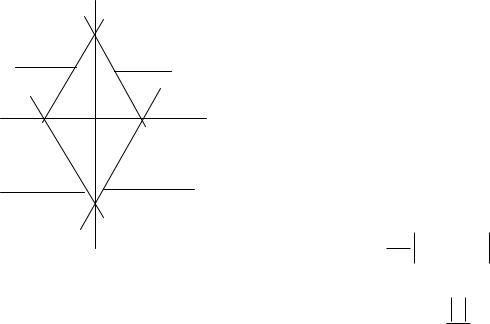
		Перейдем		к	новым				координатам

		(τ, t 0 ) :
	T	t2 t1,						t1	t0		/ 2 ,
1.1	2.2	t2 t1,						t1	t0		/ 2 ,
	2.2	t0	(t2	t1) / 2,				t2	t0 / 2 .
	t0	t0	(t2	t1) / 2,				t2	t0 / 2 .
	t0	В	результате			интегрирования по
		В	результате			интегрирования по
-T/2	T/2	области,		определяемую							прямыми
		области,		определяемую							прямыми
2.1	1.2	(1.1, 1.2, 2.1, 2.2), (Рис. 1.13), получим
	-T	(1.1, 1.2, 2.1, 2.2), (Рис. 1.13), получим
	-T
					1	F		( jω)		2
				M		F		( jω)
						ξTн
Рис. 1.13				Tн
Рис. 1.13
				Tн				τ ) e j ω τ dτ.
				Bξ (τ) (1				τ ) e j ω τ dτ.
			Tн				Tн
Осуществим	предельный	переход		( Tн )					и		получим
спектральную плотность мощности Fξ (ω) случайного процесса ξ(t)


Fξ ( ω) Bξ (τ) e jω τ dτ .							(1.51)

	o	mξ и B				(τ) m2
Известно, что ξ(t) ξ(t)		mξ и B	ξ	(τ) B	0ξ	(τ) m2	. Подставим
			ξ		0ξ	ξ
значение корреляционной функции в (1.51)

Fξ ( ω) Bξ (τ) e jω τ dτ		B0ξ (τ) e jω τ dτ mξ2 e jω τ dτ

F	( ω) m2	δ(ω) .					(1.52)
0ξ	ξ

Из (1.52) следует, что спектральная плотность не центрированного случайного процесса имеет составляющую m2 , характеризующую мощность постоянной составляющей случайного процесса. Если процесс центрированный, то


F0ξ ( ω)					B0 ξ (τ) e j ω τ dτ		(1.53)

Функции Fξ ( ω) и F0ξ ( ω) являются						преобразованиями	Фурье от
корреляционной и			ковариационных			функций Bξ (τ) и B0 ξ (τ) .
Осуществляя обратные преобразования Фурье, получим
	1
B ξ ( τ)	1			Fξ (τ) e jω τ dω ,			(1.54)
B ξ ( τ)	2 π			Fξ (τ) e jω τ dω ,			(1.54)
	2 π

			1
B0ξ ( τ)			1		F0ξ (τ) e jω τ dω .		(1.55)
B0ξ ( τ)		2 π			F0ξ (τ) e jω τ dω .		(1.55)
		2 π

Пара преобразований (1.51), (1.54) и (1.53), (1.55) называются

преобразованиями Винера-Хинчина.
Свойства спектральной плотности мощности.
	1.	Размерность		спектральной
F( )			x 2
	плотности -		x 2
	плотности -			, где x –
			Гц

	размерность			измеряемой
	величины. Если x – электрическое
	напряжение		или	электрический
	ток,	то	Fξ (ω)	называется
0	ток,	то	Fξ (ω)	называется
0
Рис. 1.14	спектральной			плотностью
Рис. 1.14

мощности случайного процесса ξ(t) , выделяемой на сопротивлении в

Вт

1Ом, и имеет размерность . В дальнейшем под случайным

Гц

процессом ξ(t) будем понимать величину случайного напряжения

или случайного тока.
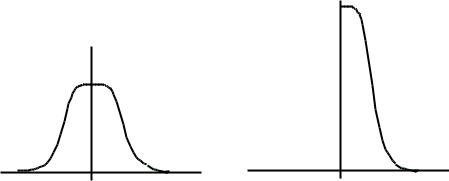
	2. Спектральная плотность мощности Fξ (ω) - неотрицательная
функция, т.е. Fξ (ω) 0,		ω .
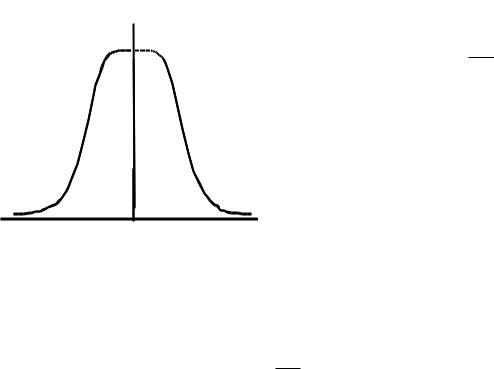
3.	Спектральная плотность мощности Fξ (ω) - функция четная,
(Рис. 1.14), т.е Fξ (ω) Fξ (ω) .
4.	Как следствие четности, имеем

	Fξ ( ω) 2 Bξ (τ) cos ω τ dτ ,		ω .
	0
5.	Мощность процесса ξ(t) будет равна

	1
Pξ B ξ ( 0)		F ξ (ω) dω	(1.56)
	2 π

6. Анализ спектральной плотности мощности,(Рис. 1.15а), по частотам в интервале частот ω очень удобен с математической точки зрения. Но в реальности физический смысл имеют частоты в интервале 0 ω . Перейдем к определению

F 0( )

F ( )



0		0
0

а)	Рис. 1.15	б)
	Рис. 1.15
	42

<<< < Предыдущая 1 2 34 / 94 5 6 7 8 9 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
22.04.201927.9 Кб0Novoe_33_1.docx
#
19.11.20191.05 Mб17Novostnaya_zhurnalistika.doc
#
24.09.201958.88 Кб2Novye_voprosy_po_fiz-re22222.doc
#
27.11.201869.54 Кб3novye_voprosy_po_UU_ot_SLM.docx
#
22.11.2019381.95 Кб2nov_kontr_po_SKD.doc
#
10.02.20151.6 Mб9Nugmanov.pdf
#
30.04.2019507.9 Кб7OAO_Tatneft.doc
#
10.09.201939.36 Кб4Obchodní a rozvojová politika.docx
#
24.04.2019290.3 Кб13Obrazovanie.doc
#
10.02.201527.6 Кб13Obrazovanie_suschestvitelnykh.docx
#
21.04.201567.6 Кб38Obrazovatelnaya_programma.docx