
напряжения относительно максимума, с помощью чего все время контролируется местоположение последнего.
Другим примером системы экстремального регулирования является система регулирования скорости двигателя внутреннего сгорания на минимум удельного расхода топлива. Статическая зависимость этого показателя от скорости двигателя имеет минимум, который смещается при изменении нагрузки, качества топлива, давления, температуры и других внешних условий. Система экстремального регулирования обеспечивает поиск и поддержание величины скорости двигателя, соответствующий минимуму расхода топлива. Аналогичная задача минимизации расхода топлива существует при регулировании двигателей самолетов при полете на большие расстояния. Здесь минимум имеется у зависимости расхода топлива на единицу пути от скорости полета, причем положение этого минимума зависит от веса самолета, высоты полета, ветра и др.
Принцип действия экстремальной системы регулирования тот же, что и контура самонастройки в САУ при оптимизации динамических режимов. Однако в связи с тем, что здесь критерий
качества является статической функцией настроечных параметров |
Y |
|
и определяется в статическом режиме, в системах экстремального регулирования не требуется пробных сигналов Gпр , которые
необходимы для определения динамических показателей качества. Что касается поисковых сигналов, то, как и у
самонастраивающейся САУ с оптимизацией динамических режимов, их также может не быть, т. е. возможны беспоисковые системы экстремального регулирования, основанные на использовании в том или ином виде уравнения статики объекта.
10.4.3. Методы поиска экстремума критерия качества.
Рассмотрим методы, с помощью которых вычислительное устройство может осуществлять поиск значений настроечных параметров Y , соответствующих экстремуму критерия качества, т. е. рассмотрим
возможные алгоритмы поиска. |
|
, |
В случае когда J является функцией одной переменной |
Y |
|
|
|
направление движения к экстремуму определяется знаком производной dJ / dY , а признаком наличия экстремума будет равенство нулю этой производной (рис. 10.8, а), т. е.
269
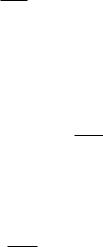
n
В общем т. е. J (Y1, Y2
dYdJ = 0.
случае, когда число настроечных параметров Y равно , Yn ) является функцией n переменных, направление
движения к экстремуму определяется градиентом, т. е. вектором
|
|
|
|
n |
J |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
grad J = ki |
Y |
, |
|
|||
|
|
|
|
i =1 |
|
|
||
|
|
|
|
|
i |
|
|
|
где ki . (i =1, 2, , n ) – единичные векторы координатных осей |
Yi . |
|||||||
В точке экстремума |
|
|
|
|
|
|
|
|
grad |
J = 0 , т. е |
J |
= 0 |
, |
i =1, 2, , n . |
|
||
Y |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
Сказанное иллюстрируется рис. 10.8, б и в для случая n = 2. |
||||||||
Метод нахождения экстремума J , |
который реализуется путем |
|||||||
изменения координат |
Y |
таким образом, что движение к экстремуму |
||||||
|
|
|
|
|
|
|
|
|
осуществляется строго по градиенту (см. траектории на рис. 10.8, б и в), называется методом градиента.
Для осуществления движения по градиенту каждая координата Yi должна изменяться со скоростью, пропорциональной значениям
соответствующих частных производных
dJ dYi
dYi
. Однако этот метод
не единственно возможный способ достижения экстремума. Существует целый ряд методов поиска экстремума, которые проще метода градиента в отношении реализации. Кроме того, как будет показано ниже, метод градиента далеко не всегда является лучшим и в отношении быстроты нахождения экстремума. Основными методами поиска экстремума, помимо метода градиента, являются метод наискорейшего спуска, метод Гаусса – Зейделя и метод случайного поиска.
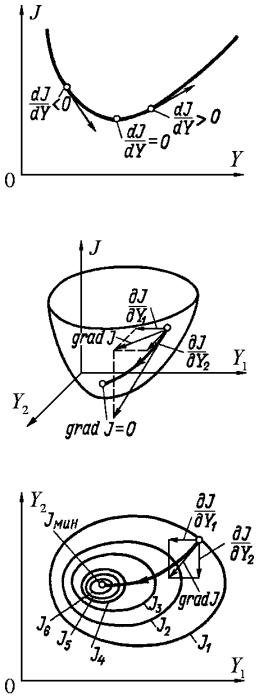
Метод наискорейшего спуска состоит в следующем (рис. 10.9,
траектория 2). В начальной точке находится направление вектора grad J , и организуется движение в этом направлении до тех пор, пока
не прекратится уменьшение J (в случае поиска минимума), т. е. не обратится в нуль производная от J по принятому направлению движения. Как видно из рис. 10.9, этому моменту соответствует касание траектории с линией J = const. B этой точке касания вновь определяется направление вектора grad J , и движение продолжается
по этому новому направлению опять до момента изменения знака
270
приращения
J
и т. д.
а
б
в
Рис. 10.8. Метод градиента
Таким образом, метод наискорейшего спуска проще метода градиента (кривая 1 на рис. 10.9) в том отношении, что требует определения grad J только в небольшом числе точек траектории.
271
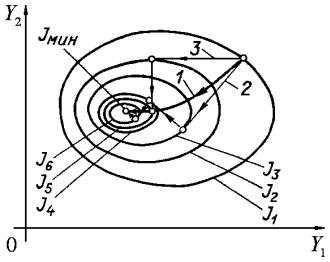
Рис. 10.9. Метод наискорейшего спуска (2) и метод Гаусса – Зейделя (3)
Метод Гаусса – Зейделя дает траекторию 3 на рис. 10.9. Он
заключается в поочередном изменении каждой из координат |
Y |
до |
|
|
момента обращения в нуль соответствующей частной производной dJ dYi . Таким образом, здесь поиск функции нескольких переменных
dYi . Таким образом, здесь поиск функции нескольких переменных
сводится к последовательному нахождению экстремума этой функции от каждой из переменных. Поэтому данный метод технически еще проще, чем метод наискорейшего спуска.
Метод случайного поиска заключается в поиске экстремума путем случайного изменения координат Yi . Из начального положения
делается случайный шаг приданиям координатам случайных приращений, и определяется приращение J . Если приращение J положительно (при поиске минимума), производится возврат в исходную точку и делается новый случайный шаг. Так продолжается до тех пор, пока не будет получено отрицательного приращения J . Тогда система переводиться в эту новую точку, и из нее производятся новые шаги, как из исходной точки.
Достоинством метода случайного поиска является отсутствие контроля зависимости J от каждой из координат Yi в отдельности.
Поэтому в отличие от рассмотренных выше детерминированных методов поиска увеличение числа координат Yi при случайном поиске
не усложняет процедуры поиска. Так, доказано, что при числе координат Yi , более трех случайный поиск по скорости достижения
экстремума превосходит градиентный метод и другие перечисленные
272
выше детерминированные методы.
Другим достоинством метода случайного поиска по сравнению с детерминированными методами является пригодность его при наличии нескольких экстремумов, из которых необходимо найти глобальный (минимум миниморум в случае поиска минимума), а также при наличии особых точек, в которых градиент J обращается в нуль. Во всех этих случаях методы, основанные на поиске точки с нулевым градиентом, непригодны, так как система может застрять на каком-либо локальном экстремуме или в особой точке. Слепой же поиск принципиальна позволяет найти все экстремумы и особые точки и выбрать глобальный экстремум.
Выбор метода поиска экстремума зависит от конкретных условий задачи. Часто оптимальным решением оказывается комбинация нескольких методов. Так, например, вдали от точки экстремума используют один метод, обеспечивающий скорейшее попадание в район экстремума, а затем переходят к другому методу. Таким образом, в частности, комбинируют метод наискорейшего спуска и метод градиента. При поиске глобального экстремума часто применяют комбинацию случайного поиска с методом градиента. В этом случае методом градиента находят локальный экстремум. Он запоминается, и затем осуществляется случайный шаг в другую произвольную точку. После этого вновь методом градиента отыскивают новый экстремум и сравнивают с ранее найденным. Число таких циклов поиска выбирают заранее, исходя из априорных данных о числе экстремумов и их взаимном размещении.
10.5. Самоорганизующиеся системы автоматического управления
Самоорганизующиеся САУ – это адаптивные САУ, в которых адаптация осуществляется путем изменения оператора, т. е структурной схемы управляющего устройства УУ основной САУ. Самоорганизующиеся САУ можно представить такой же общей функциональной схемой, как и самонастраивающиеся САУ (см. рис.
10.1). Однако здесь воздействия |
Y |
со стороны управляющего |
|
|
устройства адаптации УА на управляющее устройство УУ основной САУ вызывают изменения не численных значений параметров, а структурной схемы УУ . Поэтому самоорганизующиеся САУ
273
являются системами с переменной структурой. В самоорганизующихся САУ сигнал Y является дискретным сигналом, каждому значению которого соответствует определенный оператор УУ , т. е. определенный алгоритм управления объектом.
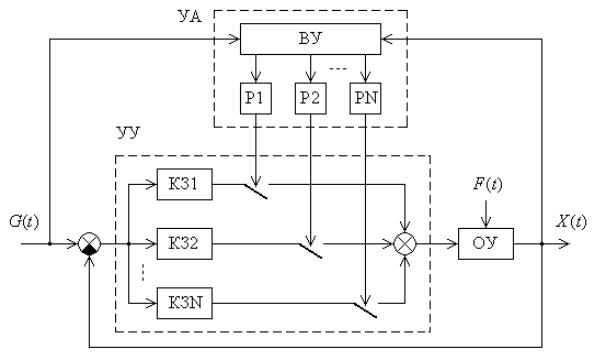
Примером простейшей самоорганизующейся САУ является самоорганизующаяся САУ с адаптивной коррекцией (рис. 10.10). Варьируемая часть УУ основной системы представляет собой набор
определенного числа корректирующих звеньев |
КЗi , которые |
включаются в контур основной САУ или отключаются исполнительными реле Рi управляющего устройства адаптации. На
рис. 10.10 условно показано, что все корректирующие звенья являются последовательными корректирующими звеньям. Задача управляющего устройства адаптации заключается в стабилизации или оптимизации принятого критерия качества управления J путем выбора определенного корректирующего звена или комбинации этих звеньев. Цепи пробного и при необходимости поискового сигналов для простоты на рисунке не показаны.
Рис. 10.10. Простейшая самоорганизующаяся САУ
Возможна комбинация описанной самоорганизующейся САУ и системы самонастройки численных значений параметров корректирующих звеньев. В этом случае появляются два этапа
274
(уровня) адаптации: первый этап – выбор структуры, т. е выбор типа коррекции (выбор определенного корректирующего звена или их комбинации), второй этап – самонастройка параметров выбранной коррекции.
Возможность изменения структуры в ходе адаптации резко расширяет диапазоны изменения свойств объекта и внешних условий, в которых самоорганизующаяся САУ сохраняет работоспособность с выполнением заданных требований к качеству управления, по сравнению с самонастраивающимися САУ, рассмотренными в предыдущей главе. Разумеется, это достигается ценой существенного усложнения контура адаптации.
10.6. Самообучающиеся системы автоматического управления
В самом общем случае под самоорганизующейся системой в кибернетике понимается система, упорядоченность, организованность которой со временем возрастают. В предельном случае такая система в исходном состоянии представляет собой совокупность элементов, связанных друг с другом совершенно случайным образом. Затем в результате взаимодействия с внешней средой постепенно в системе возникают стойкие связи между элементами, т. е. возникает определенная структура со специализацией составляющих ее элементов по выполняемым функциям. Прообразами технических самоорганизующихся систем являются живые организмы, которые, как известно, и возникли путем самоорганизации в порядке эволюции из неживой природы. Первую техническую модель самоорганизующейся системы создал английский ученый Р. Эшби (гомеостат Эшби).
Важнейшим свойством самоорганизующихся систем является их способность к обучению и самообучению. Рассмотренные в предыдущем параграфе самоорганизующиеся САУ являются простейшими САУ такого типа. Они не обладают какими-либо принципиально новыми возможностями по сравнению с самонастраивающимися системами. Однако благодаря тому, что в самоорганизующихся САУ структурная схема может целенаправленно изменяться в процессе эксплуатации, в них может быть реализована идея самоусовершенствования алгоритма работы и самого критерия качества. Такие самоорганизующиеся САУ
275
называются самообучающимися САУ. В этих системах качество управления (например, точность, если она выбрана критерием качества управления) повышается со временем в ходе эксплуатации системы.
Самообучающиеся САУ представляют собой высший тип систем автоматического управления, стоящий по своим принципиальным возможностям на уровне живых существ. Именно на базе самоорганизующихся САУ в будущем будут созданы технические системы, превосходящие по своим «мыслительным» способностям человека. Однако в настоящее время работа по созданию САУ такого типа находится еще на самом начальном этапе. Работа идет пока главным образом в направлении копирования простейших образцов живой природы.
Простейшую самообучающуюся САУ можно представить как результат автоматизации процесса усовершенствования алгоритма работы контура адаптации самообучающейся адаптивной САУ, который до автоматизации должен был осуществляться человеком по мере накопления опыта эксплуатации системы. Для этого система дополняется вторым контуром адаптации со своим управляющим устройством, который действует значительно медленнее первого контура адаптации, корректируя алгоритм последнего по результатам анализа его многократной работы в ходе эксплуатации системы. Очевидно, что управляющее устройство этого второго контура адаптации должно обязательно обладать памятью. Второй контур адаптации имеет свой критерий качества управления, для вычисления и оптимизации которого управляющее устройство этого контура воздействует на первый контур пробными и поисковыми сигналами подобно тому, как управляющее устройство первого контура адаптации воздействует на контур основной САУ.
В свою очередь, второй контур адаптации может быть дополнен еще более медленно действующим третьим контуром адаптации, улучшающим со временем алгоритм второго контура и т. д. В целом самообучающиеся САУ имеют многоступенчатую иерархическую структуру с несколькими этажами адаптации, из которых каждый последующий имеет все более обобщенный алгоритм функционирования, более медленный ритм работы и соответственно более долговременную память.
Примером самообучающейся САУ может система управления
276
роботом, когда третий, верхний уровень иерархии управления включает в себя алгоритмы коррекции и улучшения в процессе накопления опыта при эксплуатации робота первоначально заложенных типовых алгоритмов второго уровня, алгоритмов первичной обработки информации от чувствительных устройств, а также синтезируемых на третьем уровне алгоритмов выполнения отдельных заданий в случае их многократного повторения.
Вообще основной областью применения самообучающихся САУ являются именно такие сложные объекты с принципиально не определимыми свойствами. Примерами таких объектов служат промышленные предприятия, большие системы телефонной связи, другие большие системы, включающие живые организмы. Управление такими объектами невозможно детерминированными управляющими устройствами. Здесь принципиально необходимо самообучающееся управляющее устройство с применением принципа распознавания образов (ситуацией) в качестве единственно возможного способа оценки состояния такого объекта.
Дальнейшим развитием адаптивных систем автоматического управления являются системы искусственного интеллекта.
10.7. Контрольные вопросы
1.Какие системы управления называются адаптивными?
2.В чем отличие адаптивных САУ от неадаптивных?
3.Виды адаптивных САУ.
4.Каким типом звена представляется исполнительное устройств
вконтуре самонастройки самонастраивающихся САУ?
5.Виды самонастраивающихся САУ с оптимизацией качества управления.
6.Какова цель самонастройки?
7.Какие САУ называются беспоисковыми?
8.Достоинства беспоисковых самонастраивающихся САУ.
9.Какие САУ называются поисковыми?
10.Основные методы поиска экстремума.
11.Какие САУ называются самоорганизующимися?
12.Достоинства самообучающихся систем.
277
