
студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy
.pdf7.8 ] |
Интерферометры и интерферометрия |
561 |
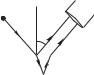
костей или газов. Пучки света, прошедшие через щели 91 и 92 и кюветы 1 и 2, заполненные исследуемыми жидкостями или газами, собираются объективом Л2 и образуют в его фокальной плоскости интерференционную картину. От разности хода волн, прошедших через кюветы 2 1 зависит смещение интерференционных полос ( — длина кювет, 1 и 2 — показатели преломления в кюветах 2 и 1). Измеряя смещение полос, можно определить разность показателей преломления .
Широко распространенный в настоящее время метод изучения спектрального состава излучения основан на использовании интерферометра Майкельсона (см. рис. 7.13 д), в котором одно из зеркал перемещается в процессе измерения.
При использовании монохроматического источника интенсивность света, регистрируемого фотоприемником Ф (расположенном в фокальной плоскости объектива Л2), равна
: 2:0 1
7
(см. формулу (7.8)). Пусть одно из зеркал перемещается со скоростью , разность хода интерферирующих волн изменяется:2 . Тогда
: 2:0 1 2
7
Частота изменения тока фотоприемника : равна2 , т. е. оптической частоте излучения соответствует измеряемая частота фототока.
Если источник содержит несколько монохроматических компонент различных частот , то ток фотоприемника также будет содержать несколько соответствующих компонент .
Таким образом, с помощью подвижного зеркала в интерферометре Майкельсона спектр, расположенный в области оптических частот, содержащихся в источнике света, трансформируется в фотоприемнике в низкочастотный спектр (в область радиочастот).
Например, при ( 4 1015 Гц ( 2$(), что соответствует зеленой линии оптического спектра и скорости перемещения зеркала 1 см/с, частота фототока 7 2,4 105 Гц. Изучая спектральный состав фототока, можно судить о спектре излучения источника.
Описанный метод исследования оптических спектров называется фурье-спектрометрией, поскольку на последней стадии
измерений определяется спектр (преобразование Фурье) фототока.
562 |
Интерференция волн |
[ Гл. 7 |
Вопросы и задачи
1.Проанализируйте работу интерференционных схем, показанных на рис. 7.13. Какие параметры схем определяют ширину интереференционной полосы и апертуру интерференции?
Чем определяется минимальный порядок интерференции в схеме Ллойда
ив интерферометре Майкельсона?
2.В какой из схем на рис. 7.13 возникают наиболее сильные ограничения на степень монохроматичности и на размеры источника.
3.Радиоизлучение космического источника длины волны , имеющего угловой размер F, принимается антенной, расположенной на отвесном берегу на
высоте над уровнем моря. Как будет меняться интенсивность принимаемого сигнала в зависимости от угла возвышения источника над горизонтом . При каких значениях F интенсивность не зависит от ?
Поверхность воды можно рассматривать как плоское зеркало, считать углы
и F малыми.
4.Три плоские монохромотические волны с амплитудами 1, и 1 падают на плоскость 0 под углами 0, и так, что колебания в точке0 оказываются синфазными. При смещении плоскости наблюдения в область E 0 происходят периодические изменения контраста интерференционной картины. Объясните явление. Найдите положение плоскости наблюдения, в которых контраст картины максимален и минимален. Чему он равен?
5.Излучающая система состоит из ряда равноотстоящих параллельных вибраторов с линейно меняющейся вдоль ряда разностью фаз излучения. Как должен меняться со временем сдвиг фаз между двумя соседними вибраторами, чтобы главный лепесток диаграммы направленности всей системы (т. е. главный дифракционный максимум) совершал круговой обзор местности с постоянной угловой скоростью (при отсутствии вращения самой решетки
|
|
вибраторов). |
|
|
6. С помощью зрительной трубы, установленной на |
|
S |
бесконечность, наблюдают полосы равного наклона в тон- |
|
кой плоскопараллельной пластинке толщиной 0,2 мм |
|
с показателем преломления 1,41. При этом угол |
||
|
|
наблюдения $ может изменяться от 0 до 90Æ (рис. 7.24). |
|
|
Найти максимальный и минимальный порядок интерфе- |
|
|
ренционных полос. Оценить допустимую степень моно- |
|
Рис. 7.24 |
хромотичности , при которой будут четко наблюдаться |
|
все интерференционные полосы. Каков допустимый раз- |
|
|
|
|
|
|
мер источника в этом эксперименте для 500 нм? |
|
7. Каково минимальное угловое разрешение радиоинтерферометра, уста- |
|
новленного на Земле, при работе на длине волны 10 м? |
||

Г л а в а 8
ДИФРАКЦИЯ
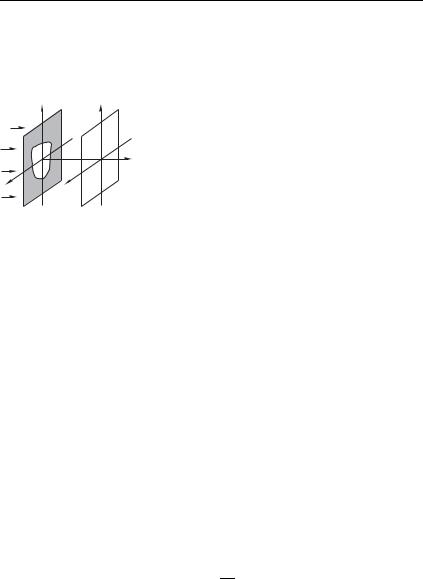
Дифракцией называют совокупность волновых явлений, в которых проявляются отклонения от законов геометрической оптики. Пусть, например, непрозрачный экран с круглым отверстием освещается параллельным пучком света. В плоскости наблюдения, расположенной недалеко от экрана, можно наблюдать картину, показанную на рис. 8.1 а: равномерно освещенное круглое пятно с резкой границей света и тени, в точности повторяющее размеры и форму отверстия, т. е. изображение получается
геометрическим проецированием отвер- |
|
|
|
стия на плоскость наблюдения. Однако |
|
|
|
стоит отнести плоскость наблюдения по- |
|
|
|
дальше (рис. 8.1 б), и наблюдаемая кар- |
|
|
|
тина существенно изменяется: граница |
|
|
|
света и тени становится размытой, а |
à |
á |
|
внутри пятна возникают чередующиеся |
|||
|
Рис. 8.1 |
||
светлые и темные кольца. Наконец, если |
|
||
|
|
плоскость наблюдения отнести еще дальше и (или) уменьшить размеры отверстия, через которое прошел свет, то размер освещенного пятна в плоскости наблюдения становится существенно больше размеров отверстия — мы видим явное нарушение геометрического закона прямолинейного распространения света.
Итак, нам нужен рецепт, который позволил бы описывать законы распространения волн, отличные от законов геометрической оптики.
В этой главе мы будем рассматривать строго монохроматические волны с заданной частотой . Как и при изучении интерференционных явлений, будем описывать волновой процесс скалярной функцией
- , , |
(8.1) |
в которой и — функции координат, определяющие пространственную структуру волны. Напомним, что монохроматической волне можно поставить в соответствие комплексную амплитуду 7 D , которая (при заданной частоте) со-
держит всю необходимую информацию о волне. Эту функцию координат мы будем называть далее волновым полем (или просто
полем).
564 |
|
|
Дифракция |
[ Гл. 8 |
||
Постановка простейшей дифракционной задачи такова. Пусть |
||||||
непрозрачный |
экран |
(маска) |
с |
отверстием, |
расположенный |
|
в плоскости 0, освещается волной, созданной источниками, |
||||||
расположенными слева от экрана, в области ' 0. Требуется |
||||||
определить |
волновое |
поле справа от экрана, в области & 0 |
||||
|
|
|
(рис. 8.2), в частности, в плоскости на- |
|||
x |
|
|
блюдения П, расположенной на расстоя- |
|||
|
|
|
нии от экрана. |
|
||
|
|
z |
Для решения этой задачи необходимо |
|||
O |
|
найти ответ на два основных вопроса. |
||||
|
|
|
Первый вопрос — определение гранич- |
|||
y |
Ï |
|
ных условий — ставится следующим об- |
|||
|
|
разом: известно поле 7- , , созданное |
||||
|
|
|
||||
Рис. 8.2 |
|
в плоскости 0 (в отсутствие маски) |
||||
|
какими-либо «сторонними» источниками, |
|||||
расположенными в области ' 0. Это может быть поле плоской |
||||||
волны, нормально либо косо падающей на плоскость 0, или |
||||||
поле точечного источника — сферическая волна. Совершенно |
||||||
не важно, с помощью каких «сторонних» источников и каким |
||||||
образом это поле создано — мы его считаем заданным. Затем |
||||||
вплоскости 0 помещается непрозрачный экран с отверстием. Требуется ответить на вопрос, какое поле 70 , возникает
вплоскости, непосредственно примыкающей к экрану с отверстиием справа от него (эту плоскость далее будем называть
плоскостью 0 ).
Это и есть то граничное условие, которое необходимо знать для решения дифракционной задачи.
Второй вопрос: каким образом, зная граничное поле 70 , , определить искомое поле 7 , , в области & 0 (т. е. в пространстве справа от экрана)? В частности, каково поле в фиксированной плоскости наблюдения & 0?
Основными параметрами, существенно определяющими характер дифракционных явлений, являются: длина волны , размер отверстия , расстояние до плоскости (или до точки) наблюдения . Как показывает дальнейший анализ (см. § 8.3–8.7),
тот или иной характер дифракционных явлений существенно зависит от значения волнового параметра
8 )
Область значений волнового параметра 8 1 называется областью геометрической оптики. Область значений 8 1 — областью дифракции Фраунгофера (или дальней волновой зоной). Промежуточная область 8 1 — областью дифракции Френеля
(или ближней волновой зоной).
8.1 ] |
Граничные условия Кирхгофа |
565 |
8.1. Граничные условия Кирхгофа
Определение граничных условий представляет собой исключительно трудную проблему. Действительно, пусть речь идет об электромагнитной волне, падающей на проводящий экран с отверстием. Переменное электрическое поле волны порождает на проводящем экране переменные токи, которые в свою очередь индуцируют «вторичную» электромагнитную волну. Эта волна зависит как от физических свойств экрана, так и от геометрии отверстия. Суммарное волновое поле в плоскости 0 представляет собой суперпозицию первичной волны (поля сторонних источников) и вторичной волны, индуцированной токами проводимости, причем электрическое и магнитное поля суммарной волны должны удовлетворять известным в электродинамике граничным условиям. Имеется лишь небольшое число задач, для которых найдено точное решение (например, задача дифракции на идеально проводящем шаре).
Мы, следуя немецкому физику Г. Кирхгофу (1824–1887), определим приближенные граничные условия следующим об-
разом: в той части плоскости 0 , которая затенена непрозрачным экраном, граничное поле полагается равным нулю. На открытой части волнового фронта (т. е. в области отверстия) граничное поле полагается равным полю сторонних источников. Другими словами, в этой области установка экрана с отверстием совершенно не влияет на падающую волну. Итак, граничное поле определяется следующим равенством:
|
7- , в точках , , принадлежащих |
|
70 , &% |
отверстию, |
(8.2) |
|
0 в точках, затененных маской. |
|
Еще раз 'подчеркнем, что граничные условия (8.2) являются
приближенными: наличие экрана в действительности приводит к тому, что поле на отверстии отлично от падающего поля 7- , , и особенно сильно оно искажено вблизи краев отверстия; да и в затененной области поле отлично от нуля вблизи краев.
Однако, как показывает сравнение теоретических выводов, основанных на приближенных граничных условиях Кирхгофа, с экспериментом, согласие оказывается удовлетворительным при условии, что, во-первых, линейные размеры отверстия велики по сравнению с длиной волны и, во-вторых, плоскость наблюдения находится на расстоянии, много большем длины волны:
& , ,
566 |
Дифракция |
[ Гл. 8 |
причем первое неравенство не обязательно должно быть сильным.
Равенству (8.2) можно придать другую форму, если ввести функцию пропускания непрозрачного экрана с отверстием
, согласно формуле
1 в точках , , принадлежащих отверстию ;,, 0 в точках , , лежащих вне отверстия ;.
Тогда можно записать
70 , 7- , , |
(8.3) |
Равенство (8.3) можно обобщить на случай произвольного тонкого экрана. Представим себе достаточно тонкую плас-
тинку-транспарант, пропускаемость которой меняется от точки к точке по закону , , а показатель преломления (или толщина) по закону , (или , ).
Пусть такая пластинка освещается плоской нормально падающей волной. Что происходит с волной на выходе из пластинки в плоскости 0 ? Переменная поглощательная способность транспаранта приводит к тому, что амплитуда колебаний на выходе будет не константой, а некоторой функцией координат , . Переменный показатель преломления или толщина приводят к различному в разных точках набегу фазы, , так что фронт прошедшей волны будет не плоским: распределение фаз колебаний на выходе будет описываться функцией , .
Если ввести комплексную пропускаемость транспаранта со-
гласно формуле
, , D , ,
то комплексная амплитуда волны на выходе из пластинки может
быть найдена по той же формуле (8.3), которая и определяет граничное поле 70 , для произвольного тонкого экра-
на.
Принципиально важным оказывается то обстоятельство, что влияние маски затрагивает лишь пространственные характеристики волнового поля, не меняя его частоту (а в случае немонохроматических волн — частотный спектр). Это — общее свойство линейных и стационарных оптических систем.
Приведем примеры амплитудных и фазовых транспарантов,
часто применяемых в оптике.
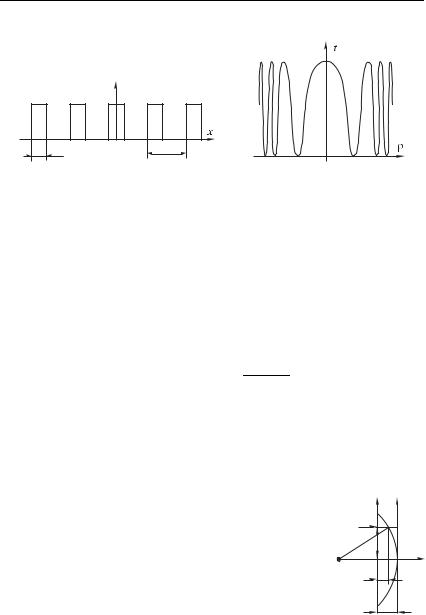
1. Дифракционная решетка имеет функцию пропускания
|
|
8/ , |
(8.4) |
8.1 ] |
|
Граничные условия Кирхгофа |
|
567 |
|||||
изображенную на рис. 8.3 ( — период решетки, 2 — ширина ще- |
|||||||||
ли, 2! 1 — число штрихов). |
|
|
|
|
|
||||
|
|
t |
|
|
|
|
|
|
|
|
2b |
|
d |
|
|
|
|
|
|
|
|
Рис. 8.3 |
|
|
|
Рис. 8.4 |
|
||
|
2. Амплитудная синусоидальная решетка с периодом |
|
|||||||
2$ и глубиной модуляции |
|
|
|
|
|||||
|
|
1 |
|
|
(8.5) |
||||
|
3. Фазовая синусоидальная решетка — |
|
|
|
|||||
|
|
|
D |
|
|
|
(8.6) |
||
(Это пример чисто фазовой структуры: амплитуда волны про- |
|||||||||
шедшей через решетку не меняется, а фаза изменяется по сину- |
|||||||||
соидальному закону.) |
|
|
|
|
|
|
|||
|
4. Зонная решетка Габора (рис. 8.4) — |
|
|
|
|||||
|
|
3 1 2 |
2 |
, |
|
(8.7) |
|||
|
|
|
|
0 3 |
|
|
|
||
где 32 2 2, 0 . |
|
|
|
|
|
||||
|
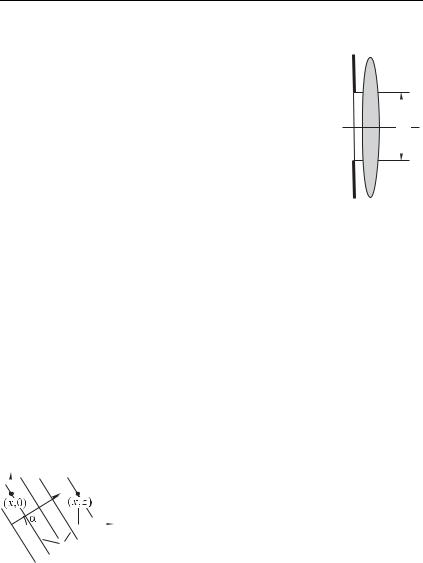
5. Функция пропускания линзы. Основным элементом любой |
||||||||
оптической системы (фотоаппарат, микроскоп, телескоп) являет- |
|||||||||
ся линза. Рассмотрим тонкую прозрачную пластинку, одна из по- |
|||||||||
верхностей которой плоская, а другая — сферическая радиуса |
|||||||||
(рис. 8.5). Считая линзу тонкой, мы полагаем, |
x |
x |
|||||||
что распространение волны через линзу проис- |
|||||||||
|
|
||||||||
ходит по законам геометрической оптики, т. е. |
S |
|
|||||||
чтобы связать световое поле в точке на входе |
R x |
|
|||||||
в линзу (в плоскости 0 ) с полем в той же |
0 |
|
|||||||
точке на выходе (в плоскости 0 , примы- |
0 |
0 z |
|||||||
кающей к линзе справа), достаточно найти набег |
|
|
|||||||
фазы вдоль луча 9, проходящего через линзу на |
|
||||||||
0 |
|||||||||
расстоянии от оптической оси. |
|
|
|||||||
|
Луч, |
проходящий |
вдоль |
оптической |
оси |
Рис. 8.5 |
|||
( |
0) |
приобретает |
набег |
фазы, |
равный |
||||
|
|
||||||||
0 |
0 ( — показатель преломления, 0 — толщина линзы |
||||||||
на оптической оси — расстояние между плоскостями, примыка- |
|||||||||
ющими к линзе слева и справа). Для луча 9 набег фазы равен |
|||||||||

568 Дифракция [ Гл. 8
0 — мы учитываем при этом, что часть оптического пути луч проходит внутри линзы, т. е. в среде с показателем преломления ( — толщина линзы на расстоянии от оптической оси), а другую часть пути, равную 0 , — вне линзы, т. е. в среде с показателем преломления 1. Относительный набег фазы, который только и представляет интерес,
есть
0 1 0 ,
где 0 2 2 2 2 .
Это выражение получено с помощью разложения радикала в ряд по степеням 2 и означает фактически, что сферическая поверхность линзы заменяется параболической.
Таким образом,
|
1 |
2 |
|
2, |
(8.8) |
||
2 |
|
|
22 |
||||
где через 7 обозначена величина, определяемая равенством
21 1
Она называется фокусным расстоянием линзы. В общем случае, если радиусы кривизны поверхностей 1 и 2, то вместо последнего равенства легко получить
1 |
1 |
1 |
|
1 |
|
(8.9) |
2 |
|
|
||||
1 |
|
2 |
|
|||
Эта формула хорошо известна в геометрической оптике. Будем называть линзу с описанными выше характеристиками идеальной. Проходя через идеальную линзу, волна приобретает различный в разных точках набег фазы, при этом амплитуда волны не меняется (отражением света от поверхности линзы, а также поглощением, мы пренебрегаем).
Таким образом, функция пропускания идеальной линзы определяется равенством
|
C |
2 |
(8.10) |
|
22 |
|
|
Разумеется, если мы говорим в действительности о сферических поверхностях (а не цилиндрических), то вместо (8.8) в
двумерном случае следует написать |
|
|
|||
|
|
|
2 2 , |
(8.11) |
|
|
|
||||
|
22 |
|
|
||
а вместо (8.10) |
|
|
|
|
|
, C |
2 2 |
(8.12) |
|||
|
22 |
|
|
||
8.2 ] Спектральный метод решения задачи дифракции 569
Функция пропускания связывает между собой комплексную амплитуду волны 7 , на входе в линзу с комплексной ам-
плитудой волны 7 , на выходе: |
|
|
|
|
7 , 7 , , |
(8.13) |
|
|
|
Любая реальная линза имеет конечные раз- |
|
|
||
|
|
|||
меры. Можно учесть этот факт, накрыв беско- |
|
|
||
нечную линзу с функцией пропускания (8.10) |
|
|
||
2a |
||||
непрозрачным экраном с отверстием (диафраг- |
||||
|
|
|||
мой) диаметра 2 , центр которого совпадает с |
|
|
||
центром линзы (рис. 8.6). Очевидно функция |
|
|
||
пропускания задиафрагмированной линзы имеет |
|
|
||
вид |
|
|
|
|
, 8 , C 2 2 , |
(8.14) |
Рис. 8.6 |
||
22 |
|
|
|
|
где 8 , — единично-нулевая функция,
1при 2 2 2,
8 ,
0 при 2 2 & 2
8.2. Спектральный метод решения задачи дифракции (метод Рэлея)
Перейдем к решению второй проблемы: как, зная граничное поле (8.3), найти волновое поле в области & 0. Математически проблема сводится к решению волнового уравнения, удовлетворяющего заданному граничному условию.
Рассмотрим вначале спектральный подход к решению проблемы, основанный на представлении дифрагированной волны
в виде суперпозиции плоских волн разных направлений (метод |
||||
x |
|
|
|
Рэлея). Напомним, что комплексная ампли- |
|
k |
туда плоской волны, волновой вектор k ко- |
||
|
|
|||
|
|
торой составляет угол # с осью , имеет |
||
|
|
|
|
|
0 |
|
z |
вид (4.27) |
|
|
||||
|
z |
|
7 , D ' ' , |
|
|
|
|||
|
|
|
|
|
|
|
Волновые |
|
где — амплитуда волны, # и |
|
|
поверхности |
||
|
|
Рис. 8.7 |
# — проекции вектора k на оси |
|
|
|
и соответственно (рис. 8.7). Мы рассмат- |
||
риваем для простоты случай 0, — начальная фаза, т. е. фаза колебания в точке 0, 0. Обратим внимание на чрезвычайно простое правило, согласно которому можно найти волновое поле плоской волны в любой плоскости & 0. Действительно, в плоскости 0 имеем
7 , 0 D D ',

570 Дифракция [ Гл. 8
поэтому
7 , 7 , 0 D ',
т. е. комплексные амплитуды 7 , 0 и 7 , отличаются множителем D ', определяющим набег фазы плоской волны при распространении между двумя плоскостями, разделенными промежутком (набег фазы, равный #).
Запишем, наконец, поле плоской волны в плоскости 0
в виде |
|
|
7 , 0 D7 |
, |
(8.15) |
где множитель D определяет |
как амплитуду |
, так и |
начальную фазу волны, а через 4 обозначена -компонента вектора k: # 4 (при этом -компонента вектора k есть # 2 42 ).
Обратим внимание на аналогию формулы (8.15) с выражением 7 D#, которое, как мы знаем, есть не что иное, как комплексная форма записи гармонического колебания частоты , причем комплексный множитель D определяет амплитуду колебания и его начальную фазу. На основании этой аналогии
величина 4 # может быть названа |
пространственной |
частотой. |
|
Можно сказать, что волны разных направлений # — это |
|
волны разных пространственных частот. |
|
Итак, представим граничное поле 70 в виде |
|
70 D7 |
(8.16) |
Математически выражение (8.16) полностью аналогично формуле (1.37) — представлению колебательного процесса в виде суперпозиции гармонических колебаний разных частот ; гармоническому колебанию частоты в разложении (1.37) соответствует плоская волна определенного направления #
# 4 ) в разложении (8.16).
Подчеркнем, что модуль ! всех гармоник в пространственном фурье-разложении (8.16) одинаков.
Все, что было сказано ранее по поводу возможности представления функции времени в виде суммы гармонических колебаний разных частот, можно повторить по отношению к (8.16): представлению волнового поля 70 (функции координат) в виде суммы плоских волн разных направлений — ведь математику не очень заботит различие в физическом смысле переменных (времени в (1.37) или координаты в (8.16)).
В общем случае, как мы знаем, произвольный колебательный процесс представляется в виде интеграла Фурье — непрерывной
