§2. Анализ функции f(e)

Выпишем функцию распределения Ферми-Дирака в следующем виде:

Нетрудно убедиться, что при E = E_F функция f(E) = 1/2.

Поведение функции f(E) (и электронного газа в металле) зависит от соотношения между температурой металла T и температурой Ферми (10.11).

При T << T_F (т.е. kT << E_F) электронный газ называют вырожденным и график функции f(E) незначительно отличается от ступени. В самом деле, показатель экспоненты (E - E_F) / kT будет велик по модулю всюду, за исключением интервала энергий, в котором (E - E_F) ≤ kT. При этом, если E < E_F, то (E - E_F) / kT будет величиной отрицательной и большой по модулю, значит экспонента будет близка к нулю, а f(E) ≈ 1. В случае, если E > E_F, показатель экспоненты будет большой положительной величиной и f(E) ≈ 0.

 Запишем результаты анализа в следующем виде:

Из оценок, сделанных в § 2 лекция 10, T_F ≈ 60000K, значит вплоть до T_пл - температуры плавления металлов, электронный газ вырожден (самый тугоплавкий металл, вольфрам, имеет T_пл ≈ 3693K).

При T >> T_F электронный газ называется невырожденным. В этом случае график функции f(E) идет полого спадая и уже совсем не похож на ступеньку.

На рисунке 11.2 приведены графики функции f(E) (11.4) для различных температур.

Рис. 11.2

При больших значениях энергии электронов, таких, что E - E_F >> kT, единицей в знаменателе функции f(E) (11.4) можно пренебречь, тогда для "хвоста" функции f(E) справедлива следующая формула:

что совпадает с распределением Максвелла-Больцмана (см. Ч. 3, (2.14)).

Итоги лекции n 11

1. Зависимость среднего числа фермионов в одном квантовом состоянии <n(E_i)> от их энергии и температуры называется распределением Ферми-Дирака (см. (11.1)):

        здесь Е_F - уровень Ферми, параметр распределения, который определяют из условия нормировки. Другое название этого параметра - химический потенциал, который принято обозначать греческой буквой µ, т.е. E_F ≡ µ.

2. При не очень высоких температурах, когда kT<<E_F для уровня Ферми  справедливо приближенное выражение (см. (11.3)):

         здесь E_F(0) - энергия Ферми.

3. Так как среднее число фермионов в одном квантовом состоянии изменяется от 0 до 1, т.е. в тех же пределах, что и вероятность f(E_i) заполнения данных квантовых состояний, то для f(E_i) справедлива формула (11.1а), аналогичная формуле (11.1):

4. Анализ функции f(E) при Т=0 К дает следующие результаты:

5. При больших значениях энергии электронов, таких, что Е-Е_F>>kT, для "хвоста" функции f(Е) справедлива формула (11.5):

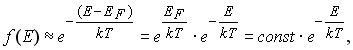
что совпадает с распределением Максвелла-Больцмана.

ЛЕКЦИЯ N 12

Результаты квантовой теории электропроводности. Термоэлектронная эмиссия. Бозоны. Распределение Бозе-Эйнштейна

§ 1. Результаты квантовой теории электропроводности металла

В Ч. 4 настоящего курса  была приведена  формула (6.9) для σ - удельной проводимости, полученная П. Друде в рамках классической теории электропроводности:

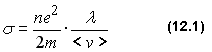
Из распределения Максвелла следует, что средняя скорость движения электрона в металле <v> пропорциональна корню квадратному из абсолютной температуры, т.е.

ЛЕКЦИЯ N 12

§ 3.  Бозоны. Распределение Бозе-Эйнштейна

Бозон - это частица или (квазичастица - как, например, фонон - квант упругих колебаний в твердых телах) с нулевым или целочисленным спином. К бозонам, как уже упоминалось, относятся также фотоны (спин s = 1), составные  частицы,  состоящие  из  четного  числа  фермионов  (например,  атом ⁴₂He), куперовские пары электронов, образование которых приводит к сверхпроводимости.

Распределение Бозе-Эйнштейна дает <n(E_i)> среднее число невзаимодействующих между собой бозонов в состоянии с энергией E_i , где i - набор квантовых чисел, характеризующих квантовое состояние. Формула распределения Бозе-Эйштейна имеет следующий вид:

где µ - химический потенциал; T - абсолютная температура; k - постоянная Больцмана.

В отличие от распределения Ферми-Дирака в знаменателе стоит "минус единица". Вследствие этого химический потенциал µ для бозонов не может быть положительным. Иначе при E_i < µ (если бы µ > 0!) показатель экспоненты в знаменателе стал бы отрицательным, экспонента стала бы меньше единицы и некоторые из чисел заполнения n_i стали бы отрицательными, что невозможно.

Если полное число частиц в системе не фиксировано, как, например, для фотонов при тепловом излучении, то химический потенциал µ равен нулю.

При фиксированном числе частиц величину µ определяют из условия нормировки, как и в случае распределения Ферми-Дирака.

Применим распределение Бозе-Эйнштейна для вывода формулы Планка для u(ω, Т) - функции распределения плотности энергии в спектре излучения абсолютно черного тела.

При обычных, не лазерных, интенсивностях фотоны можно считать невзаимодействующими между собой бозонами, поэтому тепловое излучение, находящееся в равновесии со стенками излучающей полости можно рассматривать как идеальный фотонный газ.

Как было отмечено выше, химический потенциал для системы фотонов µ = 0. Энергия фотона , следовательно,  распределение Бозе-Эйнштейна для фотонов имеет следующий вид:

здесь <n(ω_i)> - среднее число фотонов с частотой ω_i. Частота ω_i  задает квантовое состояние фотона.

Пусть ΔE обозначает энергию фотонов, находящихся в объеме ΔV и имеющих частоты, лежащие в интервале Δω.

Тогда

имеет смысл функции распределения плотности энергии в спектре излучения абсолютно черного тела (спектральное распределение).

Пусть ΔZ(ω_i) - число квантовых состояний фотонов в объеме ΔV и интервале частот от ω_i до ω_i + Δω.

Тогда

так как произведение   дает среднюю энергию фотонов частоты ω_i, т.е. среднюю энергию в одном квантовом состоянии. Функция <n(ω_i)> известна, поэтому задача состоит в нахождении числа квантовых состояний ΔZ(ω_i).

Подсчет числа квантовых состояний ΔZ делается с использованием формулы (10.5), т.е.:

здесь двойка учитывает две возможные поляризации фотонов. Фазовый объем.

где - объем сферического слоя в пространстве импульсов.

Импульс фотона (см. (5.3)):

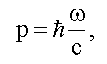
значит

Тогда

Так как частоты ω_i меняются квазинепрерывно, то мы опустили индекс i, нумерующий квантовые состояния.

Подставляя в формулу (12.11) для ΔE полученное выражение ΔZ(ω) (12.12) и функцию распределения Бозе-Эйнштейна для фотонов (12.9), получим:

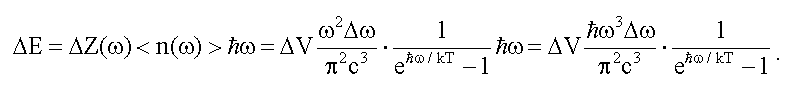
Используя это выражение, получим формулу Планка для функции распределения плотности энергии в спектре излучения абсолютно черного тела:

 

Из нее, как показано в лекции N 2, § 1, следует формула для спектральной плотности энергетической светимости абсолютно черного тела (см. (2.1), (2.2)).