
- •3. Элементы кинематики
- •3.1. Материальная точка, система материальных точек, абсолютно твердое тело - простейшие физические модели
- •3.1.1. Материальная точка
- •3.1.3. Абсолютно твердое тело
- •3.2. Тело отсчета
- •3.3. Система отсчета
- •3.8.1. Скорость направлена по касательной к траектории
- •3.8.2. Компоненты скорости
- •3.9. Вычисление пройденного пути
- •3.10.1. Нормальное и тангенциальное ускорение
- •6. Кинематика вращательного движения
- •6.1. Поступательное и вращательное движение
- •6.2. Псевдовектор бесконечно малого поворота
- •6.5. Связь линейной скорости материальной точки твердого тела и угловой скорости
- •4. Динамика материальной точки
- •4.6.1. Система си (System international)
- •4.6.1.1. Размерность силы
- •4.7. Третий закон Ньютона
- •5. Законы сохранения
- •5.1. Механическая система - это совокупность тел, выделенных нами для рассмотрения 5.1.1. Внутренние и внешние силы
- •5.2. Закон сохранения импульса
- •5.6.1. Консервативность силы тяжести
- •5.6.2. Неконсервативность силы трения
- •5.7. Потенциальная энергия может быть введена только для поля консервативных сил
- •5.8.Закон сохранения механической энергии
- •7. Динамика вращательного движения
- •8. Элементы специальной теории относительности
- •8.2. Принцип относительности Галилея:
- •8.3. Неудовлетворительность механики Ньютона при больших скоростях
- •Принцип постоянства скорости света:
- •8.5.1. Вывод преобразований Лоренца
- •Электричество
- •9. Постоянное электрическое поле
- •9.3. Электрическое поле
- •9.3.6. Принцип суперпозиции электрических полей
- •9.3.7. Напряженность поля точечного заряда
- •9.3.8. Линии напряженности
- •9.4.2.2. Заряд в произвольном месте внутри сферы
- •9.4.2.4. Поток вектора е поля системы зарядов, находящихся внутри замкнутой поверхности
- •9.4.2.5. Поток вектора е для поля, созданного зарядами, находящимися вне замкнутой поверхности
- •9.4.3. Формулировка теоремы Гаусса
- •9.4.4.1. Поле равномерно заряженной бесконечной плоскости
- •9.9. Проводник в электрическом поле
- •9.10. Электроемкость уединенного проводника
- •9.11. Электроемкость конденсатора
- •9.12. Энергия электрического поля
- •9.12.1. Плотность энергии электрического поля в вакууме
- •9.13. Электрическое поле в диэлектрике
- •9.13.1. Диэлектрик?
- •9.13.1.1. Два типа диэлектриков - полярные и неполярные
- •9.13.2. Поляризованность диэлектрика (вектор поляризации) - это дипольный момент единицы объема:
- •9.13.4.1. Плотность энергии электрического поля в диэлектрике
- •10. Постоянный электрический ток
- •10.1. Сила тока
- •10.2. Плотность тока
- •10.2.1. Связь плотности тока и скорости упорядоченного движения зарядов
- •10.4. Закон Ома для участка цепи
- •10.5. Закон Ома в дифференциальной форме
- •10.6. Закон Джоуля-Ленца в дифференциальной форме
- •Магнетизм. Уравнения Максвелла
- •11. Магнитное поле в вакууме
- •11.2. Проводник с током создает только магнитное поле, другой проводник с током реагирует только на магнитное поле
- •11.3. Рамка с током как регистратор магнитного поля. Вектор магнитной индукции
- •11.5.6. Магнитное поле тороида
- •11.6. Закон Ампера
- •11.7. Сила Лоренца - это сила, действующая со стороны магнитного поля на движущийся в нем заряд
- •11.7.1. Движение заряженной частицы в однородном магнитном поле
- •11.11.1. Потокосцепление
- •11.11.2. Индуктивность соленоида
- •11.11.3. Энергия магнитного поля
- •12. Магнитное поле в веществе
- •12.2. Классификация магнетиков
- •13. Уравнения Максвелла
- •13.1. Первая пара уравнений Максвелла в интегральной форме
- •13.1.1. Первое уравнение первой пары - это закон Фарадея-Ленца
- •13.1.2. Второе уравнение первой пары - нет магнитных зарядов
- •13.2. Вторая пара уравнений Максвелла в интегральной форме
- •13.3. Система уравнений Максвелла в интегральной форме
- •13.4. Система уравнений Максвелла в дифференциальной форме
- •Литература,
- •14.1.1.4. График гармонического колебания
- •14.2 Дифференциальное уравнение гармонических колебаний
- •14.2.1 Колеблющиеся системы
- •14.3.2. Сложение колебаний одинаковой частоты и одинакового направления
- •14.3.3. Сложение колебаний близких частот
- •14.3.4. Сложение взаимно-перпендикулярных колебаний
- •14.4. Затухающие колебания
- •14.4.1. Колеблющиеся системы
- •14.4.5. Дифференциальное уравнение, описывающее затухающие колебания наших двух систем в этих обозначениях будет иметь один и тот же вид
- •14.4.6. Решение
- •14.4.7. Проверка
- •14.5.5. Дифференциальное уравнение, описывающее вынужденные колебания
- •14.5.6. Решение дифференциального уравнения
- •14.5.6.1. Частное решение неоднородного уравнения
- •14.5.6.1.1. Векторная диаграмма
- •14.5.6.1.2. Резонанс
- •16. Электромагнитные волны
- •16.1. Система уравнений Максвелла для плоской электромагнитной волны
- •16.1.1. Поперечность электромагнитных волн
- •16.1.2. Волновое уравнение
- •16.5.1.1. Вероятностное истолкование электромагнитной волны
- •17. Геометрическая оптика
- •17.1. Законы геометрической оптики
- •17.1.1. Закон прямолинейного распространения света
- •17.1.2. Закон независимости световых лучей
- •17.1.3. Законы отражения и преломления
- •17.2. Полное внутреннее отражение
- •17.3. Тонкие линзы
- •17.3.1. Собирающие и рассеивающие линзы
- •17.3.2. Фокусы линзы, фокальная плоскость
- •17.3.3. Фокусное расстояние тонкой линзы
- •17.3.4. Построение изображения в линзах
- •18.2. Способы получения когерентных источников
- •18.2.1. Опыт Юнга
- •18.2.2. Зеркала Френеля
- •18.2.3. Бипризма Френеля
- •18.2.4. Интерференция при отражении от прозрачных пластинок
- •18.2.4.1. Кольца Ньютона
- •18.3. Многолучевая интерференция
- •19. Дифракция света
- •19.1 Дифракция Френеля и Фраунгофера
- •19.2. Принцип Гюйгенса-Френеля
- •19.2.1. Математическая формулировка принципа Гюйгенса-Френеля
- •19.3. Зоны Френеля
- •19.3.1. Дифракция Френеля на круглом отверстии
- •19.3.2. Дифракция Фраунгофера на щели
- •19.3.2.1. Таутохронность линзы и ее следствия
- •19.3.2.2. Определение положений максимумов и минимумов методом зон Френеля
- •19.3.2.3. Зависимость интенсивности дифракционной картины от угла дифракции φ
- •19.4 Дифракционная решетка
- •19.4.1. Условие главного максимума для дифракционной решетки
- •19.4.2. Зависимость интенсивности дифракционной картины решетки от угла дифракции φ
- •19.4.2.1. Минимумы интенсивности дифракционной картины решетки
- •19.4.2.2. Добавочные минимумы, ближайшие к главным максимумам
- •19.4.3. График интенсивности Ip(Sinφ )
- •19.4.4. Дифракционная решетка как спектральный прибор
- •19.4.4.1. Угловая дисперсия дифракционной решетки
- •19.4.4.2. Линейная дисперсия
- •19.4.4.3. Разрешающая сила дифракционной решетки
- •19.4.4.3.1. Критерий Релея
- •19.4.4.4. Разрешающая сила решетки для цуга волн. Соотношение между длиной цуга δx и точностью определения волнового числа δk.
- •20. Поляризация света
- •20.1. Плоско поляризованная электромагнитная волна
- •20.2. Принцип действия поляризатора электромагнитной волны
- •20.2.1. Поляроид
- •20.3. Закон Малюса
- •20.3.1. Частично поляризованный свет. Степень поляризации
- •20.4. Эллиптическая и круговая поляризация
- •20.5. Поляризация при отражении и преломлении
- •20.5.1. Формулы Френеля
- •20.5.2. Закон Брюстера
- •20.6. Двойное лучепреломление
- •20.6.1. Модель двояко преломляющего кристалла
- •20.6.1.1. Необыкновенный и обыкновенный луч
- •21. Взаимодействие света с веществом
- •21.1. Дисперсия света
- •21.1.1. Классическая электронная теория дисперсии
- •21.1.1.1. Связь показателя преломления с дипольным моментом молекулы
- •21.1.1.2. Связь дипольного момента молекулы с напряженностью поля световой волны
- •21.1.1.2.1. Простейшая модель атома в поле световой волны
- •21.1.1.2.2. Уравнение движения электрона и его решение
- •21.1.1.2.3. Проекции дипольного момента и напряженности поля волны на ось X
- •21.1.1.3. Выражение для n2
- •21.1.1.4. Анализ зависимости n(ω)
- •21.2.1. Связь групповой скорости u с фазовой скоростью V
- •14 Декабря 1900 г. Считают датой рождения квантовой физики.
- •Лекция n 1 § 2. Тепловое излучение
- •Лекция n 1 § 3. Излучение абсолютно черного тела. Закон Кирхгофа.
- •Итоги лекции n 1
- •Немецкий физик Макс Планк в 1900 г. Выдвинул гипотезу, согласно которой электромагнитная энергия излучается порциями, квантами энергии. Величина кванта энергии (см. (1.2):
- •Лекция n 2 Проблема излучения абсолютно черного тела. Формула Планка. Закон Стефана-Больцмана, закон Вина § 1. Проблема излучения абсолютно черного тела. Формула Планка
- •§ 2. Закон Стефана-Больцмана и закон Вина
- •Итоги лекции n 2
- •Лекция n 3
- •Проблема фотоэффекта. Уравнение Эйнштейна для фотоэффекта
- •§ 1. Проблема фотоэффекта
- •Фотоэффект - это испускание электронов веществом под действием электромагнитного излучения.
- •1) Наибольшее воздействие оказывают ультрафиолетовые лучи;
- •2) Сила тока возрастает с увеличением интенсивности света, освещающего фотокатод;
- •3) Испущенные под действием света заряды имеют отрицательный знак.
- •2) Максимальная кинетическая энергия электронов, у фотокатода, (mv2max)/2, прямо пропорциональна частоте V света, освещающего фотокатод.
- •Лекция n 3 § 2. Уравнение Эйнштейна для фотоэффекта
- •Итоги лекции n 3
- •Лекция n 4 Боровская теория атома водорода Спектр излучения атома водорода в теории Бора § 1. Боровская теория атома водорода
- •Первый постулат Бора: Существуют стационарные состояния атома, находясь в которых он не излучает электромагнитных волн.
- •Условие стационарности состояния атома - квантование момента импульса электрона l.
- •Лекция n 4 § 2. Спектры излучения атома водорода в теории Бора
- •Итоги лекции n 4
- •Корпускулярно-волновой дуализм микрообъектов
- •1. Скорость фотона всегда постоянна и равна скорости света в вакууме.
- •2. Масса фотона
- •3. Энергия фотона
- •4. Импульс фотона
- •§ 3. Интерференция одиночных фотонов
- •Но опыт показывает, что с течением времени на экране наблюдения формируется интерференционная картина с тем же самым расположением максимумов и минимумов, как и при большой интенсивности света.
- •§ 4. Вероятностная интерпретация плотности энергии и интенсивности электромагнитной волны
- •Итоги лекции n 5
- •Лекция n 6 § 2. Дифракция одиночных электронов
- •§ 3. Волновая функция и волна де Бройля
- •Лекция n 6 § 4. Соотношения неопределенностей
- •Соотношения неопределенностей являются следствием корпускулярно-волнового дуализма квантовых объектов.
- •Итоги лекции n 6
- •§ 2. Понятия об операторах физических величин
- •Лекция n 7 § 3. Решение уравнения Шредингера для простейших случаев: свободная частица и частица в бесконечно глубокой одномерной потенциальной яме
- •Плотность вероятности обнаружения частицы:
- •Итоги лекции n 7
- •§ 2. Квантовые числа
- •Лекция n 8 § 3. Спектры атома водорода в теории Шредингера
- •§ 4. Волновая функция основного состояния атома водорода
- •Итоги лекции n 8
- •Волновые функции ψnlm(r, θ, φ) стационарных состояний атома водорода определяются тремя квантовыми числами:
- •§ 2. Физические основы периодической системы элементов д. И. Менделеева
- •Лекция n 9 § 3. Молекула
- •§ 4. Объяснение температурной зависимости теплоемкостей газов
- •Итоги лекции n 9
- •Элементы физики ядра и элементарных частиц
- •Лекция n 16 § 2. Дефект массы и энергия связи атомного ядра. Ядерные силы
- •1. Слияние (синтез) легких ядер в одно ядро;
- •2. Деление тяжелых ядер на несколько более легких ядер.
- •Итоги лекции n 16
- •§ 3. Ядерный реактор
- •Лекция n 17 § 4. Реакция синтеза атомных ядер. Проблема управляемых термоядерных реакций
- •Итоги лекции n 17
- •§ 2. Закон радиоактивного распада
- •Лекция n 18 § 3. Взаимодействие радиоактивного излучения с веществом
- •Лекция n 18 § 4. Методы регистрации ионизирующих излучений
- •Итоги лекции n 18
- •§ 1. Электронный газ в модели одномерной бесконечно глубокой ямы
- •Лекция n 10 § 2. Электронный газ в модели бесконечно глубокой трехмерной потенциальной ямы
- •Итоги лекции n 10
- •Квантовая теория свободных электронов в металле для модели трехмерной потенциальной ямы (см. § 2) дает следующую формулу для энергии Ферми (см (10.10)):
- •Оценки дают для ef(0) значение около 5 эВ. Элементы квантовой статистики
- •Лекция n 11
- •§2. Анализ функции f(e)
- •Итоги лекции n 11
- •Итоги лекции n 12
- •Квантовая теория электропроводности металлов дает для удельной проводимости σ формулу (12.2):
- •Введение в зонную теорию твердых тел лекция n 13 Происхождение энергетических зон в кристаллах. Металлы, диэлектрики и полупроводники в зонной теории. Собственная проводимость полупроводников
- •§ 1. Происхождение энергетических зон в кристаллах. Металлы
- •§ 2. Диэлектрики и полупроводники
- •Лекция n 13 § 3. Собственная проводимость полупроводников
- •Итоги лекции n 13
- •Если самая верхняя - валентная - зона заполнена наполовину, то она является зоной проводимости. Такие кристаллы относятся к металлам. Все металлы хорошо проводят электрический ток.
- •Донорные примеси, полупроводники n-типа
- •§ 2. Акцепторные примеси. Полупроводники p-типа
- •Лекция n 14 § 3. Электронно-дырочный переход. Полупроводниковый диод
- •§ 4 . Полупроводниковый триод - транзистор
- •Итоги лекции n 14
- •Основы физики лазеров лекция n 15
- •§ 1. Вводные сведения
- •§ 2. Вынужденное (стимулированное) излучение
- •§ 3. Состояние с инверсией населенности
- •Лекция n 15 § 4. Оптический резонатор
- •§ 5. Способы создания инверсии населенности
- •Лекция n 15 § 6. Виды лазеров и их применение
- •2) Резонансное воздействие на атомы, молекулы и молекулярные комплексы, вызывающие процессы фотодиссоциации, фотоионизации, фотохимические реакции.
- •Итоги лекции n 15
- •Список литературы, использованный при написании II части конспекта лекций по физике
5.6.1. Консервативность силы тяжести


![]()
На
приведенном выше рисунке дан вид сбоку.
Точка m
движется
под действием силы тяжести из 1 в 2. Сила
тяжести всегда направлена вниз!
![]() вектор
перемещения,
вектор
перемещения,
![]() .
.
При любой траектории ответ будет таким же, значит, сила тяжести консервативна.
5.6.2. Неконсервативность силы трения
|
На рисунке
изображен вид сверху на материальную
точку m,
движущуюся при наличии силы трения
из положения 1 в положение 2.
Сила
трения всегда направлена против
скорости
|

 .
.
Ответ зависит от выбора траектории, значит, сила трения неконсервативна.
5.7. Потенциальная энергия может быть введена только для поля консервативных сил
Так как их работа не зависит от траектории, а только от начального и конечного положений материальной точки, то эту работу можно записать в виде разности двух чисел: одно - Wn1 - будет зависеть от начального положения тела, второе - Wn2 - от конечного положения тела.
![]() .
.
Wn1 - потенциальная энергия тела в положении 1; Wn2 - в положении 2.
5.7.1. Некоторые конкретные выражения для потенциальной энергии Wn(r) Для нахождения конкретного вида зависимости Wn(r) необходимо вычислить работу
![]() .
.
В
частности, для однородного поля тяжести,
где
![]() ,
используя (5.6.1),
получим: Wn
= mgh.
Если
,
используя (5.6.1),
получим: Wn
= mgh.
Если
![]() -
гравитационная сила, то
-
гравитационная сила, то
![]() Если
Если
![]() -
кулоновская сила, то
-
кулоновская сила, то
![]() .
Если
.
Если
![]() -
сила упругости, то
-
сила упругости, то
![]() .
.
5.8.Закон сохранения механической энергии
5.8.1.Для одной материальной точки, движущейся в поле консервативных сил, из (5.5)
A12 = Wk2 - Wk1,
из (5.7)
A12 = Wn1 - Wn2.
Откуда
Wn1 - Wn2 = Wk2 - Wk1
или
Wk1 + Wn1 = Wk2 + Wn2.
В поле консервативных сил сумма кинетической и потенциальной энергии материальной точки остается постоянной, т.е. сохраняется.
![]() -
полная энергия материальной точки.
-
полная энергия материальной точки.
Полная энергия материальной точки в поле консервативных сил сохраняется.
5.8.2. Полная энергия системы материальных точек Для системы, состоящей из N взаимодействующих между собой материальных точек, полная энергия
 ,
,
где Wп i, k - потенциальная энергия взаимодействия i -й материальной точки с k-й материальной точкой. Wп - потенциальная энергия взаимодействия всех частиц системы между собой.
5.8.2.1. Закон сохранения энергии для системы материальных точек Если система материальных точек находится во внешнем поле консервативных сил, то её полная механическая энергия
![]() ,
,
где W'п - потенциальная энергия системы во внешнем поле. Полная механическая энергия системы материальных точек, находящейся только под действием консервативных сил, остается постоянной. При наличии неконсервативных сил полная механическая энергия системы не сохраняется, ее убыль равна работе неконсервативных сил.
7. Динамика вращательного движения
7.1. Работа при вращательном движении. Момент силы

Из (5.3.2):
![]() ,
,
![]() .
.
Mz - момент силы Ft относительно оси вращения z. В векторном виде:
![]() -
векторное произведение.
-
векторное произведение.
7.2. Кинетическая энергия при вращательном движении. Момент инерции
![]() .
.
![]() .
.
Iz - момент инерции твердого тела, относительно оси z.
Моментом инерции материальной точки Ii называется величина:
![]() .
.
Следовательно,
![]() .
.
Величина I зависит от положения оси вращения и от распределения масс в теле.
7.2.1. Теорема Штейнера

![]() ,
,
где I0 - момент инерции относительно оси OО, I - момент инерции относительно оси O'О'.
7.2.2. Моменты инерции I0 для некоторых тел
Обруч: |
|
где R - радиус обруча. |
Диск: |
|
где R - радиус диска. |
Шар: |
|
где R - радиус шара. |
Стержень: |
|
где l - длина стержня. |
|
|
m - масса тела. |
7.3. Уравнение динамики вращательного движения Из (5.5):
![]() .
.
Используем (7.1) и (7.2):
 .
.
Используем (6.3):
![]() ,
,
Откуда
![]() .
.
Получим основное уравнение динамики вращательного движения, сравнить с (4.6):
![]() .
.
7.4. Момент импульса абсолютно твердого тела Из (7.3):
![]() ,
или
,
или
 .
.
Введем момент импульса абсолютно твердого тела:
![]() .
.
В векторном виде для однородного симметричного тела:
![]() .
.
Закон изменения момента импульса со временем:
 ,
сравнить с (4.6)
,
сравнить с (4.6)
7.5. Закон сохранения момента импульса Из (7.4):
![]() ,
,
если
момент силы
![]() =
0, то:
=
0, то:
![]() .
.
Т.к.
![]() ,
то величина
,
то величина
![]() будет
иметь одинаковые значения для любых
интересующих нас моментов времени, т.
е.:
будет
иметь одинаковые значения для любых
интересующих нас моментов времени, т.
е.:
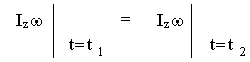 ;
;
или
![]() .
.
Вращающееся тело может изменить свой момент инерции, изменится и его угловая скорость, но при равенстве нулю суммарного момента внешних сил величина Izω останется постоянной. Пример - фигурист в "волчке".


