3702
.pdf
|
(2,1) |
|
|
2 |
|
dq |
L2 |
mz |
|
iqz |
0 |
nz |
|
iqz |
|
|
|
||||
|
Bmn |
( ) |
|
|
|
|
G0 |
(q, ) dzsin |
L |
e |
|
dz sin |
L |
|
e |
|
|
|
|
||
|
L |
2 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
2 |
|
|
|
0 |
2 |
|
|
L |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
2 2mn |
dq |
|
|
|
|
1 ( 1)m cosqL1 ( 1)n cosqL2 ( 1)m n cosq(L1 |
L2 ) |
|
||||||||||||
|
L1L22 |
|
G0 |
(q, ) |
|
|
|
|
|
|
|
. |
|||||||||
2 |
|
|
[( m L2 )2 |
q2][( n L1)2 |
q2] |
|
|
||||||||||||||
В выражениях (8), (9) числа m и n – одновременно четные или нечетные, также заметим, что эти выражения совпадают с выражением для матричных элементов в случае одиночного дислокационного сегмента [2-5].
Соотношение (7) представляет собой уравнение колебаний двух смежных отрезков дислокации разной длины в матричном виде. Из этого уравнения получим для амплитудного спектра смещений двух смежных отрезков дислокации
|
(1) |
|
|
|
(1,1) |
|
(1,2) |
1 |
|
|
(1) |
|
Q |
|
|
B |
|
B |
|
|
|
F |
|
. |
|
Q(2) |
|
B(2,1) |
B(2,2) |
|
F(2) |
|
||||||
|
B |
(1,1) |
B |
(1,2) |
1 |
|
Следовательно, блочная матрица |
|
|
|
является функцией ли- |
||
B(2,1) |
B(2,2) |
|
|
|||
нейного отклика (обобщенной восприимчивостью) двух смежных отрезков дислокации. Уравнение, определяющее собственные частоты колебаний этих отрезков, имеет вид
|
(1,1) |
|
|
(1,2) |
|
|
det B |
|
( ) |
B |
|
( ) |
0. |
B(2,1)( ) |
B(2,2)( ) |
|||||
Согласно известной формуле [7], запишем это равенство в виде произведения определителей обычных матриц
B(1,1) |
|
B(2,2) B(2,1) (B(1,1) ) 1B(1,2) |
0, |
где B(1,1) 0. Таким образом, получим уравнение на собственные колебания
двух смежных отрезков дислокации
B(2,2) B(2,1)(B(1,1) ) 1B(1,2) |
0. |
Аналогичные результаты получены ранее в работах [8-14] при исследовании колебаний дислокационных сегментов.
Литература
1. Батаронов И.Л. Влияние центров пиннинга и рельефа Пайерлса на обобщенную восприимчивость дислокаций в реальных кристаллах / И.Л. Батаронов, В.В. Дежин, А.М. Рощупкин // Изв. РАН. Сер. Физическая. 1993. Т. 57. № 11. С. 97-105.
2. Батаронов И.Л. Обобщенная восприимчивость дислокационных осцилляторов / И.Л. Батаронов, В.В. Дежин // Физико-математическое моделирование систем: материалы II Междунар. семинара. Воронеж: ВГТУ, 2005. Ч. 1. С. 105-114.
30
3.Батаронов И.Л. О колебаниях дислокационного сегмента / И.Л. Батаронов, В.В. Дежин // Вестник Тамбовского университета. 2013. Т. 18, вып. 4, часть 2. С. 1566-1567.
4.Батаронов И.Л. О решении интегрального уравнения, описывающего динамику закрепленной дислокации / И.Л. Батаронов, В.В. Дежин // Матер. Междунар. открытой конф. «Современные проблемы анализа динамических систем. Приложения в технике и технологиях». В сб. научных тр. «Актуальные направления научных исследований XXI века: теория и практика». Воронеж: УОП ФГБОУ ВПО «ВГЛТА». 2014. № 4, часть 2. С. 65-68.
5.Bataronov I.L. The generalized susceptibility of dislocation segment in nondissipative crystal / I.L. Bataronov, V.V. Dezhin // J. of Physics: Conf. Ser. 2016. V. 738. N 1. 012108. doi:10.1088/1742-6596/738/1/012108.
6.Краснов М.Л. Интегральные уравнения / М.Л. Краснов. М.: Наука, 1975. 304 с.
7.Гантмахер Ф.Р. Теория матриц. / Ф.Р. Гантмахер. М.: Наука, 1966. 576 с.
8.Батаронов И.Л. Об уравнении колебаний двух смежных дислокационных сегментов одинаковой длины / И.Л. Батаронов, В.В. Дежин // Современные методы прикладной математики, теории управления и компьютерных технологий. Сб. тр. VII Междунар. науч. конф. Воронеж: Научная книга. 2014. С. 27-29.
9.Батаронов И.Л. Матричные элементы дислокационных осцилляторов при колебаниях двух смежных дислокационных сегментов разной длины / И.Л. Батаронов, В.В. Дежин // Современные методы прикладной математики, теории управления и компьютерных технологий. Сб. тр. VIII Междунар. науч. конф. Воронеж: Научная книга. 2015. С. 54-56.
10.Батаронов И.Л. Об уравнении колебаний двух смежных дислокационных сегментов разной длины / И.Л. Батаронов, В.В. Дежин // Сб. матер. VI Междунар. конф. «Деформация и разрушение материалов и наноматериалов». М.: ИМЕТ РАН. 2015. С. 862-864.
11.Дежин В.В. О колебаниях двух смежных дислокационных сегментов / В.В. Дежин
//«Физическое материаловедение»: VII Междунар. шк.: сб. матер. Тольятти: Изд-во ТГУ. 2016. С. 75-77.
12.Дежин В.В. Математическое моделирование изгибных колебаний двух смежных дислокационных сегментов одинаковой длины / В.В. Дежин // Физико-математическое моделирование систем: материалы XV Междунар. семинара. Воронеж: ВГТУ. 2016. Ч. 2. С. 64-67.
13.Дежин В.В. О решении интегрального уравнения, описывающего колебания двух смежных дислокационных сегментов / В.В. Дежин // Математические методы в технике и технологиях – ММТТ-29: сб. тр. XXIX Междунар. науч. конф. Т.3. Саратов: СГТУ. 2016. С. 5-7.
14.Дежин В.В. О колебаниях двух смежных отрезков линейных дефектов в сплошной изотропной среде / В.В. Дежин // Механика деформируемого твердого тела: сб. тр. IX Всеросс. конф. Воронеж: Изд-во «Научно-исследовательские публикации». 2016. С. 4-6.
MATHEMATICAL MODELING OF BENDING VIBRATIONS TWO ADJACENT DISLOCATION SEGMENTS OF THE DIFFERENT LENGTH
V.V. Dezhin
Voronezh State Technical University
Integral equation of two dislocation segments vibrations in view of fixing conditions is written down. Solution for the dislocation displacement is sought in the form of a series. The equation of oscillation of two adjacent dislocation segments written in matrix form. Expressions for the matrix elements of dislocation oscillators are found. An equation describing the eigenvibrations of two adjacent dislocation segments is obtained
Keywords: dislocation segment, bending vibrations, the matrix elements of dislocation oscillators, eigenvibrations equation
31
УДК 548.4
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ИЗГИБНЫХ КОЛЕБАНИЙ ВИНТОВОЙ ДИСЛОКАЦИИ В ПРОИЗВОЛЬНОЙ ПЛОСКОСТИ СКОЛЬЖЕНИЯ ВБЛИЗИ ТОЧКИ СТРУКТУРНОГО ФАЗОВОГО ПЕРЕХОДА
В.В. Дежин1, В.Н. Нечаев2
1Воронежский государственный технический университет 2ВУНЦ ВВС «Военно-воздушная академия имени профессора Н.Е. Жуковского и Ю.А. Гагарина», Воронеж viktor.dezhin@mail.ru
Записана система уравнений, описывающая колебания винтовой дислокации в произвольной плоскости скольжения вблизи точки структурного фазового перехода. Найден Фурье-образ проекции силы Пича-Келера на плоскость скольжения. Получено уравнение изгибных колебаний винтовой дислокации и функция ее линейного отклика вблизи точки структурного фазового перехода
Ключевые слова: винтовая дислокация, изгибные колебания, структурный фазовый переход, параметр порядка
Рассмотрены колебания винтовой дислокации в окрестности структурного фазового перехода. Данный переход описывался параметром порядка согласно теории Ландау [1]. Наличие дислокаций приводит к появлению добавки1(r,t) к термодинамически равновесному значению параметра порядка s , зависящей от радиус-вектора r и времени t. Ранее в работах [2, 3] была разработана общая теория математического моделирования малых колебаний дислокаций в кристаллах с мягкой модой и исследованы изгибные колебания краевой дислокации. В работе [4] найдены динамические характеристики дислокаций в кристаллах с мягкой модой. В дальнейших работах [5-11] исследовались колебания дислокаций различных ориентаций вблизи точки структурного фазового перехода. В настоящем сообщении в отличие от работ [8, 11] изучаются изгибные колебания винтовой дислокации в произвольной плоскости скольжения.
Рассмотрим винтовую дислокацию, лежащую вдоль оси Oz с единичным вектором касательной к линии дислокации 0 (0, 0, 1), вектором Бюргерса
b (0, 0, b) и единичным вектором нормали к плоскости скольжения n (nx, ny , 0). Ограничимся малыми колебаниями дислокации вблизи положе-
ния равновесия. Тогда в линейном приближении по смещению дислокации
u u(z, t) получим |
|
|
|
, 1 , |
|
|
u |
|
|
|
|
u |
||
ny z |
, nx z |
|||
( ) (x) (y) nx (x) (y)u ny (x) (y)u,
Vt ( ) 2tu2 (x) (y) nx (x) (y)u ny (x) (y)u 2tu2 (x) (y),
32
f nl lmbm nx xzb ny yzb,
(n )(b )( s 1) nxb s 2 1 nyb s 2 1 ,x z y z
ni ikbk nxb xz nyb yz 12b2 nx (x) (y) ny (x) (y) nx2 (x) (y)u n2y (x) (y)u ,ll b uz nx (x) (y) ny (x) (y) .
Здесь ( ) – двумерная -функция, – двумерный радиус-вектор, отсчитываемый от оси дислокации в плоскости, перпендикулярной вектору , V – скорость линии дислокации в данной точке, f – проекция силы Пича-Келера на плоскость скольжения, lm – тензор напряжений, ik – тензор несовместности деформаций. Подставив найденные выражения в формулы, полученные ранее [2, 3, 8, 11], будем иметь систему трех уравнений
1 |
|
2 f |
f |
|
|
|
3b |
n |
|
2 p |
n |
|
2 p |
2 gb |
n |
|
2 1 |
n |
|
2 1 |
|
|
|||
|
|
|
|
|
|
|
|
x |
|
y |
|
|
x |
|
y |
|
|
||||||||
2 |
|
t |
2 |
|
|
1 |
|
|
x z |
|
|
|
s |
x z |
|
y z |
|
||||||||
ct |
|
|
|
|
|
|
|
|
|
y z |
|
|
|
|
|
|
|
||||||||
b2 2tu2 (x) (y) b2 nx (x) (y) ny (x) (y) nx2 (x) (y)u n2y (x) (y)u , (1)
1 |
|
2 p |
p 4 1 g |
|
1 |
|
2 1 |
|
|
|
|
|
|||||||||||
2 |
|
|
|
|
|
|
|
||||||||||||||||
|
t |
2 |
|
|
3 1 |
s 2 |
|
t |
2 |
|
|
1 |
|
|
|
||||||||
cl |
|
|
|
|
|
ct |
|
|
|
|
|
|
|
|
|
||||||||
|
|
2 |
1 |
b |
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2) |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
31 |
z |
nx (x) (y) ny (x) (y) , |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1(r, t) 3 sg (r |
|
|
|
|
|
|
|
. |
(3) |
||||||||||||||
r |
,t t )p(r |
,t )dr dt |
|
||||||||||||||||||||
В этих уравнениях обозначено ct и cl – скорости поперечных и продольных звуковых волн, – коэффициент Пуассона, p – гидростатическое давление,– модуль сдвига, g – постоянный стрикционный коэффициент, – плотность вещества кристалла, (r,t) – функция отклика параметра порядка на гидростатическое давление. Для решения записанной системы совершаем преобразование Фурье уравнений (1)-(3) по r и t:
q2 ct22 f 13b (nxqx nyqy )qz p 2 bg s (nxqx nyqy )qz 1
|
b |
2 2 2 |
2 2 |
2 |
2 |
b |
2 |
(nyqx |
nxqy ) (qz ) ( ), |
(4) |
|||||||
|
nyqx |
nxqy |
c2 |
u i(2 ) |
|
||||||||||||
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
q2 2 |
cl2 p |
4 |
1 |
g s q2 |
2 |
ct2 1 |
2 |
1 |
|
b(nxqx nyqy )qzu |
, |
(5) |
|||||
|
|
|
|||||||||||||||
|
|
31 |
|
|
|
|
31 |
|
|
|
|
||||||
|
|
|
|
|
1 3g s p. |
|
|
|
|
|
|
|
|
|
(6) |
||
33
Здесь q – |
волновой вектор, |
– |
|
частота, |
f (q, ), |
p(q, ), |
|
|
(q, ), |
u(q, ), |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
(q, ) |
0 |
2 ( 2 q2 |
2 ) |
[12] – Фурье-образы, |
2 |
a(T T ) – квадрат ха- |
||||||||||||||||||||||||||
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
c |
|
|
|
|
|
рактерной частоты мягкой моды, Tc |
– температура структурного фазового пере- |
|||||||||||||||||||||||||||||||
хода, ~ c2 . Исключая из системы |
(4)-(6) |
p и |
|
|
|
, для проекции силы Пича- |
||||||||||||||||||||||||||
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Келера получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
f (q, ) |
|
|
2 |
b2(nx2qx2 |
ny2q2y )qz2 1 2(1 ) g2 2s u |
|
|
|
|
|||||||||||||||||||||
|
|
1 |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
2 |
|
|
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||||||
|
|
|
|
|
2 |
|
2 |
|
g |
2 |
2 |
|
2 |
|
2 |
|
|
|
|
|||||||||||||
|
|
|
|
q |
|
2 |
q |
|
|
2 |
4 |
1 |
|
s |
q |
|
|
2 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
ct |
|
|
|
|
cl |
|
|
|
|
|
|
|
|
|
|
ct |
|
|
|
|
|
||||
|
|
|
(n2q2 n2q2 2 |
|
c2 )u i(2 )2(n |
q |
x |
n |
q |
y |
) (q |
z |
) ( ) |
|
||||||||||||||||||
|
|
b2 |
y x |
|
x |
y |
|
|
|
t |
|
|
|
y |
|
|
x |
|
|
|
|
|
|
. |
(7) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
q2 2 ct2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Находим выражение для проекции силы Пича-Келера на линии дислокации (x=0, y=0). Для этого совершим обратное преобразование Фурье выражения
(7) по переменным qx и qy, а затем положим x=y=0:
|
|
|
i(xqx yqy ) dqxdqy |
|
|
|
|
|||||
|
|
|
|
|
|
|||||||
f (x,y,qz, ) |
f (q, )e |
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
(2 ) |
2 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
dqxdqy |
|
|
|||
f (0,0,qz , ) f (qz , ) |
|
f |
|
|
|
|||||||
|
(q, ) |
|
|
|
. |
(8) |
||||||
|
(2 ) |
2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|||
Переходя в интеграле (8) в полярные координаты и выполняя интегрирование по полярному углу, получим уравнение изгибных колебаний винтовой дислокации
f (qz, ) D1(qz , )u(qz, ),
где D (qz, ) – функция линейного отклика дислокации вблизи точки структурного фазового перехода, которая находится по формуле
|
|
|
|
b |
2 |
|
|
2 |
2 |
2 |
2 |
2 |
2 |
|
|
1 |
|
|
|
|
|
(ny |
nx |
)q |
|
ct |
|
||
|
|
(q |
, ) |
|
|
q dq |
|
|
|
|
|
|
|
|
|
4 |
|
q2 |
2 ct2 |
|
|
||||||||
|
D |
z |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
2 |
2 |
1 2(1 ) g |
2 |
|
2 |
|
|
|
|
||||
|
2 |
|
(nx |
ny )q qz |
|
s |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||
1 (q2 2 c2 )(q2 |
2 |
c |
2 ) 4 |
1 |
g2 2 |
(q2 2 |
c2 )2 |
|||||||||||
|
|
|||||||||||||||||
|
|
|
t |
|
|
l |
|
1 |
|
s |
|
|
|
t |
|
|||
В случае собственных колебаний дислокации необходимо решать уравнение D1(qz, ) 0, из которого находятся собственные частоты изгибных колебаний дислокации в окрестности структурного фазового перехода и их затухание, можно установить влияние взаимодействия упругого поля с мягкой модой на эффективную массу и эффективную жесткость дислокации.
Полученный результат может быть использован для исследования затухания и рассеяния ультразвука, электромагнитных волн и других внешних воздействий на кристалл с дислокациями.
34
Литература
1.Ландау Л.Д. Теоретическая физика. Т. 5. Статистическая физика. Ч. 1. / Л.Д. Ландау, Е.М. Лифшиц. М.: Наука, 1976. 584 с.
2.Дежин В.В. Обобщенная восприимчивость дислокации в кристалле с мягкой модой / В.В. Дежин, В.Н. Нечаев, А.М. Рощупкин // Физика твердого тела. 1990. Т. 32. № 3. С. 810-817.
3.Dezhin V.V. Generalized susceptibilily of dislocations in ferroelectrics and ferromagnetics / V.V. Dezhin, V.N. Nechaev, A.M. Roshchupkin // Zeitschrift für Kristallographie. 1990. V.193. P.175-197.
4.Батаронов И.Л. Динамические характеристики дислокаций в кристаллах с мягкой модой / И.Л. Батаронов, В.В. Дежин, В.Н. Нечаев // Изв. РАН. Сер. Физическая. 1998. Т. 62,
№8. С. 1512-1517.
5.Нечаев В.Н. Математическое моделирование колебаний дислокаций в кристаллах с мягкой модой / В.Н. Нечаев, В.В. Дежин // Современные проблемы прикладной математики, теории управления и математического моделирования: матер. V Междунар. конф. Воронеж: Издательско-полиграфический центр ВГУ, 2012. С. 213-215.
6.Нечаев В.Н. Система уравнений, описывающих динамику дислокации смешанного типа вблизи точки структурного фазового перехода / В.Н. Нечаев, В.В. Дежин // Физикоматематическое моделирование систем: матер. IХ Междунар. сем. Воронеж: ВГТУ, 2012. Ч.1. С. 63-66.
7.Нечаев В.Н. Уравнение изгибных колебаний дислокации вблизи точки структурного фазового перехода / В.Н. Нечаев, В.В. Дежин // Математические методы в технике и технологиях: сб. тр. XXVII Междунар. научной конф. Саратов: СГТУ, 2014. Т. 1. С. 48-50.
8.Нечаев В.Н. Система уравнений, описывающих изгибные колебания винтовой дислокации вблизи точки структурного фазового перехода / В.Н. Нечаев, В.В. Дежин // Физикоматематическое моделирование систем: матер. ХI Междунар. сем. Воронеж: ВГТУ, 2014. Ч. 2. С. 45-48.
9.Нечаев В.Н. Математическое моделирование изгибных колебаний дислокации произвольной ориентации вблизи точки структурного фазового перехода / В.Н. Нечаев, В.В. Дежин // Матер. Междунар. конф. «Актуальные проблемы прикладной математики, информатики и механики». Воронеж: Научная книга, 2014. С. 197-201.
10.Нечаев В.Н. Об уравнении изгибных колебаний дислокации смешанного типа в кристалле со структурным фазовым переходом / В.Н. Нечаев, В.В. Дежин // Физикоматематическое моделирование систем: матер. ХV Междунар. сем. Воронеж: ВГТУ, 2016. Ч. 2. С. 56-59.
11.Нечаев В.Н. Уравнение изгибных колебаний винтовой дислокации в сегнетоэластике вблизи точки структурного фазового перехода / В.Н. Нечаев, В.В. Дежин // Вестник Тамбовского университета. Сер.: Естеств. и технич. науки. 2016. Т. 21, вып. 3. С. 1188-1190.
12.Брус А. Структурные фазовые переходы / А. Брус, Р. Каули. М.: Мир, 1984. 408 с.
MATHEMATICAL MODELING OF SCREW DISLOCATIONS BENDING VIBRATIONS IN AN ARBITRARY SLIP PLANE NEAR THE STRUCTURAL PHASE TRANSITION
V.V. Dezhin1, V.N. Nechaev2
1Voronezh State Technical University
2MERC AF «Air Force Academy named after prof. N.E. Zhukovsky and Y.A. Gagarin», Voronezh
System of equations describing screw dislocation vibrations in an arbitrary slip plane near a structural phase transition is written. The Fourier transform of the Pich-Kohler force projection onto the slip plane is found. The bending vibration equation of a screw dislocation and the function of its linear response near the structural phase transition are obtained
Keywords: screw dislocation, bending vibrations, structural phase transition, order parameter
35
УДК 548.4
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ИЗГИБНЫХ КОЛЕБАНИЙ ВИНТОВОЙ ДИСЛОКАЦИИ В ПРОИЗВОЛЬНОЙ ПЛОСКОСТИ СКОЛЬЖЕНИЯ В СЕГНЕТОЭЛЕКТРИКЕ
В.В. Дежин1, В.Н. Нечаев2
1Воронежский государственный технический университет 2ВУНЦ ВВС «Военно-воздушная академия имени профессора Н.Е. Жуковского и Ю.А. Гагарина» (Воронеж) viktor.dezhin@mail.ru
Рассмотрены изгибные колебания винтовой дислокации малой амплитуды в одноосном сегнетоэлектрике, линия дислокации располагалась вдоль сегнетоактивной оси. Для решения поставленной задачи была составлена система уравнений. Получен Фурье-образ проекции силы Пича-Келера на плоскость скольжения дислокации и найдена функция линейного отклика винтовой дислокации в сегнетоэлектрике на внешнюю силу
Ключевые слова: винтовая дислокация, изгибные колебания, сегнетоэлектрик, функция отклика
Ранее в работах авторов [1-3] была разработана общая теория малых колебаний дислокаций в сегнетоэлектриках и исследованы изгибные колебания краевой дислокации. В работе [4] на основе этой теории рассмотрены изгибные колебания доменных границ в сегнетоэлектриках и сегнетоэластиках, границы моделировались дислокационной стенкой. В работе [5] найден вклад колеблющихся дислокаций в диэлектрические потери в сегнетоэлектриках. В работах [6-8] рассмотрено распределение поляризации и электрических полей вокруг колеблющейся краевой дислокации в сегнетоэлектрике. В настоящем сообщении как и в работе [9] изучаются изгибные колебания винтовой дислокации, но при этом учтена произвольность плоскости скольжения винтовой дислокации.
Рассмотрим конкретный случай винтовой дислокации в одноосном сегнетоэлектрике. Пусть сегнетоактивная ось совпадает с осью Oz: P (0, 0, P), дислокация также располагается вдоль оси Oz с единичным вектором каса-
тельной к линии дислокации 0 (0, 0, 1), вектором Бюргерса b (0, 0, b) и единичным вектором нормали к плоскости скольжения n (nx, ny , 0). Ограни-
чимся малыми колебаниями дислокации вблизи положения равновесия. Тогда в линейном приближении по смещению дислокации u u(z, t) получим
ny u z, nx u z, 1 . Наличие дислокации в сегнетоэлектрическом кри-
сталле приводит к отклонению поляризации P1 P P0 от равновесного значения P0 в однородном кристалле [1-3]. Учитывая это и предполагая изотропность
упругих и электрострикционных свойств glnkmPk Pm g1 lnP2 g2PPl n , где glnkm – тензор электрострикционных коэффициентов, получим обобщение динамиче-
36
ского уравнения Бельтрами [10] для сегнетоэлектрического кристалла с винтовой дислокацией в линейном приближении по отклонению поляризации P1:
|
|
1 2 ij |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
2 ll |
|
|
|
|
|
|
|
|
|
|
|
1 2 ll |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ij |
|
|
|
|
|
ij |
|
|
|
|
|
|
|
|
|
|
|
|
|
ij ll |
|
|
|||||||||||||||||||||
|
|
|
2 |
|
|
t |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
t |
2 |
|
1 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
ct |
|
|
|
|
|
|
|
|
2(1 ) ct |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi xj |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
(g |
|
g |
|
) |
|
P |
|
|
2P1 |
|
2 (g |
|
g |
|
)P |
|
P |
2P1 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
1 |
2 |
x x |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ij 0 |
|
t |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
ij |
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
j |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
2P1j |
|
|
|
|
|
|
2P |
|
|
|
|
|
|
|
|
2P |
|
|
|
|
|
|
2P1j |
|
|
|
|
|
|
|
2P |
|
|
|
|||||||||||||||||||||||
|
g |
2 |
P |
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
1i |
|
g |
2 |
P |
|
|
|
1 |
|
P |
|
|
|
|
|
P |
|
|
1 |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
0i |
|
|
|
t |
|
|
|
0 j |
|
|
t |
|
|
|
|
|
|
|
|
0 j |
xi z |
|
0 |
xi z |
|
|
|
0i |
|
xj z |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
P |
2P1i |
|
|
P |
P |
|
P |
P |
2P |
ij |
|
2P1 |
|
|
( j |
|
j |
ji |
|
ij |
j |
|
) 2 . |
(1) |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
0 |
xj z |
|
|
0i |
|
|
|
|
1j |
|
|
0 j |
|
|
|
|
1i |
|
|
|
|
0 |
|
|
z |
|
|
|
|
|
t |
ij |
|
|
|
|
|
|
ll |
|
|
|
|
|
ij |
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Здесь ct |
|
|
– скорость поперечного звука, |
|
– модуль сдвига, – плот- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ность вещества кристалла, ij |
– тензор напряжений, t – время, |
– коэффициент |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Пуассона, |
|
ij |
|
|
– символ Кронекера, |
2 |
x |
2 |
, |
|
j |
n bV ( ) |
n b |
j |
u t ( ) – |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
ij |
|
|
|
i j |
|
|
|
|
|
|
|
|
|
i |
|
|
|
||||||
тензор плотности потока дислокаций [11], V – проекция вектора скорости линии дислокации в данной ее точке на направление нормали к ней в плоскости
скольжения, – двумерный радиус-вектор, отсчитываемый от оси дислокации в плоскости, перпендикулярной единичному вектору касательной к линии дис-
локации |
|
в |
данной |
точке, |
( ) |
– |
двумерная |
-функция, |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ij |
ejkn |
|
ibn |
|
1 |
b in (ξ) |
|
– |
тензор несовместности деформаций [12], |
||||
|
|||||||||||||
|
|
xk |
|
2 |
|
|
|
|
|
|
|
|
|
ejkn – символ Леви-Чивитта (единичный антисимметричный тензор). Уравнение
(1) необходимо умножить на nibj , чтобы перейти к проекции силы Пича-Келера на плоскость скольжения дислокации f (r,t) ni ijbj . При этом для нашего случая расположения винтовой дислокации с учетом равенства p ll 
3 – гидростатическое давление будем иметь
ni ijbj nxb xz |
nyb yz |
f , |
|
|
(2) |
|||||||||||||
|
|
|
|
ni ijbj |
nibi 0, |
|
|
|
|
|
(3) |
|||||||
|
|
|
|
|
ni ijbj f , |
|
|
|
|
|
(4) |
|||||||
n b |
|
|
|
2 ll |
|
|
3n |
|
2 p |
3n |
|
2 p |
, |
(5) |
||||
|
|
|
|
|
x x z |
y y z |
||||||||||||
i |
j xi xj |
|
|
|
|
|
||||||||||||
|
|
|
|
2P |
|
|
|
|
2P |
|
|
2P |
|
|
|
|||
n b |
|
1 |
|
|
n |
b |
|
1 |
n |
b |
1 |
, |
|
(6) |
||||
j x x |
|
|
|
|
y z |
|
||||||||||||
i |
|
|
|
x |
|
x z |
y |
|
|
|
|
|||||||
|
|
|
|
i |
j |
|
|
|
|
|
|
|
|
|
|
|
||
37
|
|
2P1j |
|
2P |
|
||
n b |
P |
|
|
P |
|
1i |
0, |
|
2 |
|
2 |
||||
i j |
0i |
t |
0 j |
t |
|
||
|
|
|
|
|
|
||
|
|
|
2P |
|
|
|
|
|
2P1j |
|
|
2P |
|
|
2P |
|
|
||||
nibj |
P0 j |
|
|
1 |
|
P0 |
|
|
|
|
2nxbP0 |
1 |
2nybP0 |
1 |
, |
|
|
||||
x |
|
|
|
x |
|
x z |
|
|
|
||||||||||||
|
|
z |
|
|
|
z |
|
|
|
|
y z |
|
|
||||||||
|
|
i |
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
ni jijbj ninibjbj |
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
t (x) (y) nx (x) (y)u ny (x) (y) |
|
||||||||||||||||||||
n2b2 u |
(x) (y) n |
2b2 u (x) (y) b2 u |
(x) (y), |
|
|||||||||||||||||
x |
t |
|
|
|
|
|
|
|
|
|
y |
t |
|
|
t |
|
|
|
|
|
|
|
|
|
|
n j |
|
b |
|
n n bb |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
u ( ) 0, |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
i |
ji |
|
j |
|
i |
j i j |
t |
|
|
|
|
|
|
|
|
ni ijbj nxb xz nyb yz
(7)
(8)
(9)
(10)
|
|
|
|
1 |
b |
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
(11) |
||
|
|
|
2 |
|
nx (x) (y) ny (x) (y) nx |
(x) (y)u ny |
(x) (y)u . |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
После умножения на nibj и учета равенств (2)-(11) уравнение (1) примет |
|||||||||||||||||||||||||||||
вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 f |
f |
|
|
3b |
|
n |
|
2 p |
n |
|
2 p |
2 bg P |
n |
|
2P1 |
n |
|
2P1 |
|
|
||||||
|
2 |
|
|
|
x |
|
y |
|
|
x |
|
y |
|
|
|||||||||||||||
|
ct |
|
t |
|
|
|
|
|
|
1 |
|
|
x z |
|
|
y z |
|
|
|
|
x z |
|
y z |
|
|
||||
b2 2tu2 (x) (y) b2 nx (x) (y) ny (x) (y) nx2 (x) (y)u n2y (x) (y)u . (12)
Уравнение для гидростатического давления получим сверткой уравнения
(1) с учетом равенств
jii nibi ut ( ) 0, ll b uz nx (x) (y) ny (x) (y) ,
полученных для рассматриваемого в работе случая расположения винтовой дислокации. Имеем:
1 |
|
2 p |
p |
|
1 |
1 |
|
(3g g |
|
)P |
|
2P1 |
|
2 |
1 |
(2g g |
|
)P P |
|
||||||||||
c2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
t2 |
|
|
31 c2 |
|
1 |
2 |
0 t2 |
|
31 |
1 |
2 |
0 |
1 |
|
|
|||||||||||||
l |
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
|
|
2P1 |
|
|
2 |
1 |
|
u |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
g |
2P0 z2 |
|
b |
|
|
|
, |
(13) |
|||||||||||||||||
|
|
31 |
31 |
z |
nx (x) (y) ny (x) (y) |
||||||||||||||||||||||||
где cl – скорость продольного звука.
Как отмечалось в работе [9] в предположении изотропности упругих и электрострикционных свойств с учетом выбранного расположения сегнетоактивной оси следует связь поляризации с компонентой zz тензора напряжений. В случае краевой дислокации эта компонента отлична от нуля и для неподвижной дислокации и для колеблющейся. В случае прямолинейной винтовой дис-
38
локации zz 0, но у винтовой дислокации, совершающей изгибные колебания, появляется составляющие единичного вектора касательной к линии дислокацииx ny u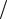
z и y nx u
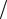z , то есть у дислокации появляется краевая ком-
понента динамической природы, создающая напряжения zz . Уравнение дляzz найдем из уравнения (1), полагая i j 3:
c1t2 2t2zz zz 1 3 21ct2 2t2p 2xp2 2yp2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2P |
|
|
|
2g |
1 |
|
2P |
|
|
2P |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
(g g |
|
)P |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
0. |
|
|
(14) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
g g |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
0 2 |
|
t |
|
|
|
|
2 |
|
|
|
|
y |
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ct |
|
|
|
|
|
|
|
1 |
|
2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Проведем преобразование Фурье уравнений (12)-(14) по r и t. Получим: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
3b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
k |
|
|
ct2 |
f |
|
|
|
|
|
|
(nxkx |
nyky )kz p 2 bg1P0(nxkx nyky )kzP1 |
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
b |
2 2 2 |
|
|
|
2 2 |
|
|
|
2 |
|
|
|
|
|
|
2 |
b |
2 |
(n |
k |
|
|
n |
k |
|
|
) (k |
|
) ( ), |
(15) |
|||||||||||||||||||||||||
|
|
|
|
nxky nykx |
|
|
ct2 |
|
u i(2 ) |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
y |
|
|
y |
|
|
x |
|
|
|
z |
|
|
|
|
|||||
|
|
|
|
|
|
2 |
|
2 |
|
1 |
|
1 |
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
(3g1 g |
2 ) |
2 |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
k |
|
|
2 |
p |
|
|
|
|
|
|
|
|
P0 4g1k |
|
2g2k |
|
2 P1 |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
cl |
|
|
|
|
3 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ct |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
1 b(nxkx nyky )kzu, |
|
|
|
|
|
|
|
|
|
|
|
|
|
(16) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
31 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
2 |
2 |
|
|
|
|
|
3 |
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2g1 |
|
|
|
|
2 |
|
|
2 |
|
||||||||||||||||||||
|
k |
|
c |
2 |
|
zz |
|
|
|
k |
|
|
|
|
|
|
p (g1 g2 )P0 |
|
|
|
|
|
k |
|
c2 |
P1 0. |
(17) |
|||||||||||||||||||||||||||||||
|
|
1 |
|
|
2c |
2 |
|
|
g1 |
g2 |
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|||
|
В уравнениях (15)-(17) k |
|
|
– волновой вектор, |
k2 |
|
kx2 |
ky2 |
– частота; |
|||||||||||||||||||||||||||||||||||||||||||||||||
f |
f (k, ), |
|
p p(k, ), |
|
P |
|
P(k, ), |
|
zz |
|
zz |
(k, ), |
|
|
u u(k |
z |
, ) – Фурье- |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
образы. Дополним записанную систему уравнений (15)-(17) уравнением, полученным ранее в работах [1-3]
P |
(k, )P ( 3g |
p g |
|
zz |
), |
(18) |
|
1 |
0 |
1 |
2 |
|
|
|
|
где (k, ) – восприимчивость сегнетоэлектрического кристалла. Решив систе-
му уравнений (15)-(18), найдем выражения для Фурье-образов f f (k, ), p p(k, ), P1 P1(k, ), zz zz (k, ). Среди этих выражений наибольший интерес представляет выражение f f (k, ), дающее связь между силой, действующей на дислокацию, и смещением дислокационной линии:
39