
3702
.pdf
УДК 538.913
РАДИАЦИОННОЕ ЗАТУХАНИЕ КОЛЕБАНИЙ ДИСЛОКАЦИОННОГО СКОПЛЕНИЯ
И.Л. Батаронов, Т.А. Надеина
Воронежский государственный технический университет nadtana@mail.ru
Проанализирован характер радиационной диссипации энергии дислокационного скопления. Установлен осциллирующий характер частотной зависимости коэффициента затухания, связанный с интерференцией упругих волн дислокаций
Ключевые слова: дислокация, диссипация
Радиационное затухание колебаний в кристалле становится существенным при низких температурах. Диссипацию энергии D за один период колебаний выразим в виде:
D Im |
2 2 |
|
2 2 |
Im * |
|
||||
|
|
|
|
|
|
, |
(1) |
||
P F P |
|
|
|
|
2 |
||||
|
|
||||||||
0 |
|
|
|
|
|
|
|
|
|
где P – диагональная составляющая матрицы функции Грина кристалла, |
|
||||||||
вектор, касательный к линии дислокации, P F P0 . Поскольку в рас-
сматриваемой постановке задачи торможение дислокации обусловлено только излучением упругих волн ускоренно движущихся дислокаций, то диссипация (1) целиком связана с радиационными потерями при колебаниях пары дислокаций.
|
|
Характер радиационной диссипации энергии колебаний зависит от соот- |
|
ношения |
частоты и волнового вектора и характеристических параметров |
||
|
r |
c r |
и r 1. В предельном длинноволновом низкочастотном случае для дис- |
|
t |
|
|
локационного диполя получаем выражение P P , в котором члены, содержащие множитель ln(q2 2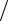 c2 ), ответственный за появление мнимой части в (1), сокращаются, и радиационное затухание в нулевом приближении отсутствует. Для пары же дислокаций одного знака будем иметь P P , что совпадает с выражением для единичной «супердислокации», имеющий «радиус ядра»
c2 ), ответственный за появление мнимой части в (1), сокращаются, и радиационное затухание в нулевом приближении отсутствует. Для пары же дислокаций одного знака будем иметь P P , что совпадает с выражением для единичной «супердислокации», имеющий «радиус ядра»

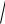 r0r , с соответствующими выводами в отношении величины диссипации (1).
r0r , с соответствующими выводами в отношении величины диссипации (1).
В другом предельном коротковолновом высокочастотном случае ( r , rqz 1) функция F 0, и мы получаем систему из двух динамически невзаимодействующих дислокаций, так что выражение (1) переходит в сумму величин диссипации для двух индивидуальных дислокаций. При этом влияние одной дислокации на другую сказывается только статически в наличии постоянного слагаемого P0, что физически эквивалентно колебанию дислокации в потенциальной яме.
В промежуточной области ( r , rq 1) не представляется возможным провести аналитическое исследование зависимости D(q, ). В то же время, из
20
выражения для функции F следует, что она представляется через бесселевы функции аргумента qr 2 ( / r )2 и, следовательно, может иметь осцилли-
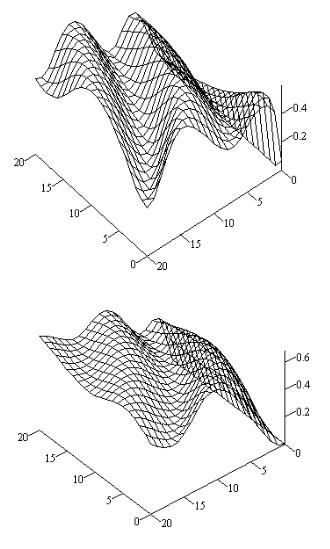
рующую частотную зависимость. Для проверки этого предположения были выполнены численные расчеты для функции D, представленные на рис. 1 и 2
которые подтверждают осциллирующий характер зависимости D(q, ) в промежуточной области.
На графиках по оси X отложено произведение r2q2 , по оси Y –
(r2 2 ) ct2 r2q2 .
ct2 r2q2 .
Физической причиной появления осцилляций является выполнение условий резонанса (антирезонанса) дислокационных колебаний, приводящее к увеличению (уменьшению) амплитуды колебаний, что, в конечном итоге, обусловлено интерференцией упругих волн колеблющихся дислокаций.
D| |
X
Y
а)
D| |
X
Y
б)
Рис. 1. Частотные зависимости диссипации энергии винтовой пары: а) диполь, б) дислокации одного знака
21
D| |
X
Y
а)
D| |
X
Y
б)
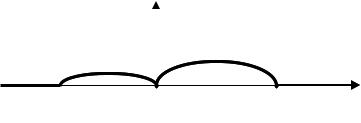
Рис. 2. Частотные зависимости диссипации энергии краевой пары: а) диполь, б) дислокации одного знака
Литература
1. Рощупкин А.М. Обобщенная восприимчивость дислокаций в диссипативном кристалле / А.М. Рощупкин, И.Л. Батаронов, В.В. Дежин // Изв. АН. Сер.Физ. – 1995. – Т.59. – №10. – С.12-17.
RADIATION DAMPING OF DISLOCATION GROUP OSCILLATIONS
I.L. Bataronov, Т.A. Nadeina
Voronezh State Technical University
The nature of the frequency dependence of radiative damping in the wavelength region on the order of the distance between dislocations and frequencies on the order of the natural frequencies of the cluster oscillations is considered
Keywords: dislocation, dissipation
22
УДК 303.732
ИНФОРМАЦИОННЫЙ АСПЕКТ ВНУТРИСИСТЕМНОГО КОНФЛИКТА
С.В. Глущенко
Военный учебно-научный центр Военно-воздушных сил «Военно-воздушная академия им. проф. Н.Е. Жуковского и Ю.А. Гагарина», Воронеж
serjvladimir@rambler.ru
Показана целесообразность разбиения всего множества параметров стохастической системы на три группы по характеру их взаимодействия. Доказывается, что наибольшую информативность содержат группы конфликтующих параметров. Из этого делается предположение о возможности исследования функционирования стохастической системы на основе анализа ядер конфликта
Ключевые слова: система, стохастичность, конфликт, плеяда, ядро, информация, информативность, коэффициент корреляции, параметр, стационарность
На первом этапе анализа функционирования стохастической системы целесообразно разбить параметры системы на группы по степени их информативности с целью выявления групп параметров, вносящих наибольший вклад в поведение системы. Оптимальное функционирование стохастической системы (СС) подразумевает, что ее параметры достигают своих оптимальных значений или варьируются вблизи своих оптимумов. Однако для большинства реальных систем наблюдается совсем иное положение вещей. Все параметры СС можно разбить на три группы:
1)группа независимых параметров;
2)группа, в которой характер взаимосвязей между параметрами можно определить как "согласие";
3)группа, в которой характер взаимосвязей между параметрами можно определить как "конфликт".
Параметры из 2-й группы отвечают тому требованию, что если воздействовать на каждый из них в направлении их оптимумов, то значения взаимосвязанных с ними параметров также приближаются к оптимальным. Напротив, для любой пары конфликтующих параметров из 3-й группы наблюдается следующее: приближение значений одного из этих параметров к своему оптимуму соответствует отдалению значений другого параметра от своего оптимума.
Параметры из 1-й и 2-й групп не вызывают проблем при оптимизации процесса. Для этих групп возможно применение хорошо разработанного аппарата скалярной оптимизации. По параметрам из 3-й группы скалярная оптимизация невозможна, в этом случае необходимо осуществить векторную оптимизацию, что гораздо более сложно. Отсюда следует, что конфликтующие параметры вызывают намного больший интерес у исследователя по сравнению с неконфликтующими.
23
В факторном анализе (в методе главных компонент) выделяются для исследования те из факторов, которые в сумме объясняют большую часть общей дисперсии исходной совокупности параметров.
При анализе функционирования стохастической системы целесообразно выделять для исследования параметры, несущие основное количество информации о системе, и отсеивать параметры малоинформативные с точки зрения исследователя. В сложных СС значительное количество параметров взаимосвязано. При этом корреляционные плеяды, включающие конфликтующие параметры (с отрицательными значениями парных коэффициентов корреляции) образуют ядра конфликта Wk, плеяды, состоящие из параметров с положительными коэффициентами корреляции образуют ядра содействия Wc, а некоррелирующие параметры можно сгруппировать в ядро безразличия Wn [1]. Практические исследования показывают, что, как правило, количество параметров из Wk превалирует в системе. Основной причиной нестационарности системы могут быть параметры как ядер конфликта, так и ядер согласия (в меньшей степени в силу того, что, можно осуществить скалярную оптимизацию параметров из Wc
иWn). Подобного эффекта, воздействуя на конфликтующие параметры, добиться невозможно. Отсюда возникает целесообразность анализа функционирова-
ния СС целесообразно основывать на исследовании конфликта.
Утверждение 1. Информативность параметра из Wk превышает информативность параметра из Wc (Wn).
Доказательство. При оптимизации СС, воздействуя на параметры из Wc
иWn, можно добиться того, что их значения будут охватывать не весь интервал варьирования, а лишь часть его ближе к оптимуму. Воздействуя на конфликтующие параметры, подобного эффекта добиться невозможно, поскольку априори неизвестна точка компромисса на множестве Парето. Поэтому конфликтующие параметры будут принимать значения на всем интервале варьирования. Сле-
довательно, дисперсия параметра из ядра содействия (безразличия) с2 ( n2)значительно меньше дисперсии параметра из ядра конфликта k2 ( с2 ( n2) << k2). Согласно [2], величина информативности непрерывной случайной величины Х, распределенной по нормальному закону, равна I=Log[(2 e)1/2 / x], где x –
предел точности |
измерения Х. Так как с2 ( n2) << k2, то величина информатив- |
ности параметра |
из ядра содействия Iс=Log[(2 e)1/2 с / x] и безразличия |
In=Log[(2 e)1/2 n/ x] будет меньше величины информативности параметра из ядра конфликта Ik=Log[(2 e)1/2 k / x].
Если рассматривать ядра конфликта, содействия и безразличия, каждое как систему, то, доказав, что информативность ядра конфликта превышает информативность ядра содействия или безразличия при равном количестве параметров в ядрах, мы будем иметь больше оснований утверждать о возможности анализа функционирования СС на основе исследования конфликта взаимодействующих параметров по сравнению с тем, что дает доказательство предыду-
щей теоремы. Обозначим k, s, n – количество параметров соответственно в Wk,
Wc, Wn.
24
Утверждение 2. Информативность Wk превышает информативность Wc
(Wn) при k s (k n).
Доказательство. Информативность ядер конфликта, содействия, безразличия определяется следующими выражениями
k |
k |
k |
|
Ik Iik , |
Ic Iic , |
In Iin . |
(1) |
i 1 |
i 1 |
i 1 |
|
Здесь Iik, Iic, Iin – соответственно приведенные величины информативности i-го параметра. Значения Iik, Iic зависят от силы связей i-го параметра с j-ми в соответствующем ядре. Необходимо выделить параметр (Хi), оказывающий наибольшее воздействие на ядро в целом. При этом, если влияние других параметров на информативность этого параметра несущественно, то информативность ядра конфликта:
k |
|
Ik Log[(2 e)1/2 1k / x1]. |
(2) |
i 1 |
|
Можно определить воздействие на Хi группы параметров как воздействие одного интегрального параметра Хj. В этом случае
fi e |
(x / |
|
r x |
|
/ |
|
)2/(2(1 r2)) |
, |
i |
ik |
ij |
j |
|
jk |
ij |
где rij – парный коэффициент корреляции Xi и Хj, ik и jk – соответствующие средние квадратические отклонения, fi – плотность вероятности. Тогда
Iik = Log[(2 e)1/2 ik (1 – ri2jk)1/2/ xi]. |
(3) |
||
Поскольку |
|
|
|
k |
k |
|
|
Ik Iik (Log[(2 e)1/2 ik (1 rijk2 )1/2 / xi ]). |
(4) |
||
i 1 |
i 1 |
|
|
Тогда |
|
|
|
|
k |
|
|
Ik |
Log[(2 e)k/2 ( ik (1 rijk2 )1/2 |
/ xi )]. |
(5) |
|
i 1 |
|
|
Для ядра согласия |
|
|
|
|
k |
|
|
Ic |
Log[(2 e)s/2 ( ic(1 rijc2 )1/2 |
/ xi )]. |
(6) |
i1
Всилу того, что ik >> ic, а величины s и k, rijk и rijc – являются величинами одного порядка, то Ik > Ic.
25
Аналогичные рассуждения можно привести при рассмотрении соотношений информативности ядер конфликта и безразличия. Ядро безразличия состоит из независимых параметров, отсюда
In Iin (Log[(2 e)1/2 1k / x1]) Log[(2 e)n/2 ( in / xi )]. |
(7) |
Так как ik >> in, a величины (1 – ri2jk)1/2 – не бесконечно малые, то Ik > In. В случае, если информативность среднего и выборочной дисперсии конфликтующего параметра больше информативности среднего и выборочной дисперсии неконфликтующего, то при определенных условиях [1] возможен анализ стационарности СС, а также анализ функционирования случайной сис-
темы, по параметрам из Wk.
Литература
1.Глущенко С.В. Синтез моделей и алгоритмов анализа функционирования стохастических технологических систем в условиях конфликта взаимодействующих параметров. Дис
…канд. техн. наук. – Воронеж: ВГТА, 1997. – 159 с.
2.Вентцель Е.С. Теория вероятностей. – М: Гос. издат. физ. – мат. литературы, 1962.
– 564 с.
INFORMATION ASPECTS OF INTRA-SYSTEM CONFLICT
S.V. Glushchenko
Military Training and Research Center of the Air Force "The Air Force Academy named after Professor N.E. Zhukovsky
and Y.A. Gagarin", Voronezh
The expediency of dividing the whole set of parameters of a stochastic system into three groups according to the nature of their interaction is shown. It is proved that groups of conflicting parameters contain the greatest information. From this it is assumed the possibility of investigating the functioning of a stochastic system on the basis of an analysis of the conflict nuclei
Keywords: system, stochasticity, conflict constellation, the core of information, the information content, the correlation coefficient, a parameter, stationarity
26
УДК 548.4
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ИЗГИБНЫХ КОЛЕБАНИЙ ДВУХ СМЕЖНЫХ ДИСЛОКАЦИОННЫХ СЕГМЕНТОВ РАЗНОЙ ДЛИНЫ
В.В. Дежин
Воронежский государственный технический университет viktor.dezhin@mail.ru
Записано интегральное уравнение колебаний двух дислокационных сегментов с учетом условий закрепления. Решение для смещения дислокации искалось в виде ряда. Уравнение колебаний двух смежных дислокационных сегментов записано в матричном виде. Найдены выражения для матричных элементов дислокационных осцилляторов. Получено уравнение, описывающее собственные колебания двух смежных дислокационных сегментов
Ключевые слова: дислокационный сегмент, изгибные колебания, матричные элементы дислокационных осцилляторов, уравнение собственных колебаний
Ранее в работе [1] получено уравнение движения бесконечной дислокации, а в работах [2-5] исследованы колебания одиночного дислокационного сегмента. В данной статье с использованием результатов работ [1-5] рассмотрены два смежных отрезка бесконечной прямолинейной дислокации в кристалле, совершающие малые колебания под действием внешней силы. Кристалл при этом моделировался сплошной изотропной средой. Линия дислокации располагалась вдоль оси Oz, смещение точек дислокационной линии (z, t) 0 при
z ( , L1) {0} [L2, ) (см. рисунок), где t – время, L1 и L2 – длины смежных отрезков дислокации. Уравнение колебаний дислокации [1] после преобразований, устраняющих расходимость функции G(z, ), для двух смежных отрезков дислокации примет вид интегрального уравнения Фредгольма первого рода:
L2 |
|
|
|
|
|
|
|
|
(1) |
dz G0 |
(z z , ) (z , ) f (z, ), |
|||
L1
где – частота, f (z, ) – величина внешней силы на единицу длины линейного дефекта, произвольная в общем случае. Функции (z, ) и f (z, ) из физиче-
ξ
z
-L1 |
L2 |
Конфигурация дислокационной линии
27

ских соображений предполагались непрерывными. Для решения задачи неизвестная функция (z, ) согласно методу неопределенных коэффициентов [6] представлялась в виде ряда по полной системе линейно независимых функцийn (z) с учетом условий закрепления дислокационных сегментов. Из физиче-
ских соображений в качестве функций n(1)(z) и n(2)(z) |
возьмем соответственно |
|||||||||||||||||
sin( nz L1) |
и sin( nz L2 ). Внешнюю силу также разложим в ряд по этой систе- |
|||||||||||||||||
ме функций: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(z, ) Qn(1)( )sin nz (L1 2 |
|
|
z L1 2 |
|
) |
|
|||||||||||
|
|
|
|
|||||||||||||||
|
n 1 |
L1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
nz (L2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Qn(2)( )sin |
|
|
|
z L2 |
2), |
|
|
|
|
(2) |
|||||||
|
|
|
|
|
|
|
||||||||||||
|
n 1 |
L2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (z, ) Fn(1)( )sin nz (L1 2 |
|
z L1 2 |
|
) |
|
||||||||||||
|
|
|
|
|||||||||||||||
|
n 1 |
L1 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
nz (L2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fn(2)( )sin |
|
z L2 |
2 |
|
). |
|
|
|
|
(3) |
|||||||
|
|
|
|
|
|
|
||||||||||||
|
n 1 |
L2 |
|
|
|
|
|
|
|
|
|
|
||||||
Здесь (x) – функция Хевисайда, обозначение (1) относится к сегменту [ L1,0],
а обозначение |
(2) – к сегменту [0,L ]. При таком разложении получается |
|
|
2 |
z 0 – точка закрепления дислока- |
f (0, ) 0, но это допустимо, потому что |
||
ционных сегментов. Подставив выражения (2) и (3) в уравнение (1), получим уравнение колебаний двух смежных отрезков линейных дефектов:
|
|
|
(1) |
|
0 |
|
|
|
|
|
|
|
nz |
|
|
|
|
|
|
||||
|
Qn |
|
( ) dz G0(z z |
, )sin |
|
L1 |
|
|
|
|
|
|
|||||||||||
|
n 1 |
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2) |
|
L2 |
|
|
|
|
|
nz |
|
|
|
|
|
|
|
(4) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Qn ( ) |
dzG0 |
(z z , )sin |
L2 |
|
f (z, ). |
|
|
|||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Умножим уравнение (4) на sin( mz L1) |
|
и проинтегрируем по z на отрезке |
|||||||||||||||||||||
[ L1, 0]: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
mz |
0 |
|
|
|
|
|
|
|
|
|
nz |
|
|
|
||
|
(1) |
( ) |
|
|
|
|
|
(z z |
|
|
|
|
|
|
|
||||||||
|
Qn |
|
dzsin |
L |
dz G0 |
, )sin |
L |
|
|
|
|||||||||||||
|
n 1 |
|
L |
|
|
|
1 |
L |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2) |
0 |
mzL2 |
|
|
|
|
|
|
nz |
|
|
|
0 |
dzsin |
mz |
f (z, ). |
(5) |
||||||
Qn |
( ) dzsin |
|
L |
dz G0(z z , )sin |
|
L |
|
|
|
L |
|||||||||||||
|
L |
|
1 |
0 |
|
|
|
|
|
|
|
2 |
|
|
|
L |
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
Затем умножим уравнение (4) на sin( mz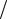 L2 ) и проинтегрируем по z на отрезке [0, L2]:
L2 ) и проинтегрируем по z на отрезке [0, L2]:
28

|
|
|
|
L2 |
|
|
mz |
0 |
|
|
|
nz |
|
|
|
|
|
(1) |
( ) dzsin |
|
|
|
|
|
|
||||||||
|
Qn |
|
L |
dz G0 |
(z z , )sin |
L |
|
|
|
|||||||
|
n 1 |
|
|
0 |
|
|
2 |
L |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
(2) |
L2 |
mzL2 |
|
|
|
|
nz |
L2 |
|
mz |
f (z, ). |
(6) |
||||
Qn |
( ) dzsin |
|
L |
dz G0 |
(z z , )sin |
L |
|
dzsin |
L |
|||||||
|
0 |
|
2 |
0 |
|
|
|
|
2 |
|
0 |
|
|
2 |
|
|
Равенства (5) и (6) запишем кратко в виде
Bmn(1,1)( )Qn(1)( ) Bmn(1,2)( )Qn(2)( ) Fm(1)( ), n 1
Bmn(2,1)( )Qn(1)( ) Bmn(2,2)( )Qn(2)( ) Fm(2)( ); n 1
или в виде произведения блочных матриц
|
|
(1,1) |
|
(1,2) |
|
|
(1) |
|
|
|
(1) |
|
|
|
B |
|
B |
|
|
Q |
|
|
|
F |
|
, |
(7) |
B(2,1) |
B(2,2) |
|
Q(2) |
|
F(2) |
|
|
||||||
где Bmn(s,t) – матричные элементы дислокационных осцилляторов, которые с учетом равенства (обратное преобразование Фурье)
G0(z z , ) 2dqG0(q, )eiq(z z )
определены следующим образом:
|
(1,1) |
|
|
|
|
2 |
|
|
|
dq |
0 |
|
|
mz |
|
iqz |
0 |
nz |
|
|
|
iqz |
|
|
|
||||||||||||||||||
|
Bmn |
|
( ) |
|
|
|
|
|
|
|
|
|
|
G0(q, ) dzsin |
L |
e |
|
|
|
dz sin L |
|
e |
|
|
|
|
|
|
|||||||||||||||
|
|
L |
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
L |
1 |
|
|
|
L |
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 2mn |
dq |
|
|
|
1 ( 1)n cosqL1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
L13 |
|
|
|
|
|
|
|
G0 |
(q, ) |
|
|
|
|
, |
|
|
|
(8) |
|||||||||||||||||||
|
|
|
|
|
|
|
2 |
[( m |
L1)2 q2 ][( n L1)2 |
q2] |
|
|
|||||||||||||||||||||||||||||||
|
(2,2) |
|
|
2 |
|
|
|
dq |
L2 |
mz |
|
|
iqz |
L2 |
nz |
|
|
iqz |
|
|
|
||||||||||||||||||||||
|
Bmn |
|
( ) |
|
|
|
|
|
|
|
|
G0(q, ) dzsin |
L |
e |
|
|
dz sin |
L |
|
e |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
L |
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
0 |
|
|
2 |
|
|
|
|
0 |
2 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
4 2mn |
dq |
|
|
|
1 ( 1)n cosqL2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
L32 |
|
|
|
|
|
G0 |
(q, ) |
|
|
|
, |
|
(9) |
||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
[( m |
L2 )2 q2][( n L2 )2 q2 ] |
|
|
||||||||||||||||||||||||||||||||
|
(1,2) |
|
|
|
2 |
|
|
|
|
dq |
0 |
|
|
mz |
|
|
|
iqz |
L2 |
nz |
|
|
iqz |
|
|
|
|||||||||||||||||
|
Bmn |
|
|
( ) |
|
|
|
|
|
|
|
G0(q, ) dzsin |
L |
e |
|
dz sin |
L |
|
e |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
L |
|
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
L |
1 |
|
|
|
|
0 |
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 2mn |
dq |
|
|
|
|
|
|
|
|
|
|
|
1 ( 1)m cosqL1 ( 1)n cosqL2 ( 1)m n cosq(L1 |
L2 ) |
|
|||||||||||||||||||||||||||
|
L12L2 |
|
G0(q, ) |
|
|
|
|
|
|
|
|
|
|
|
, |
||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
[( m L1)2 q2][( n L2 )2 |
q2] |
|
|
||||||||||||||||||||||||||||||||
29
